Área y volumen de la pirámide pentagonal elongada o sólido de Johnson J9
Proporcionamos una calculadora online del área y volumen de la pirámide pentagonal elongada (o sólido de Johnson J9), calculamos su altura y demostramos las fórmulas del área y volumen.
Índice:
- Calculadora del área y volumen
- Definición del J9
- Altura del J9
- Fórmula del área
- Fórmula del volumen
1. Calculadora del área y volumen
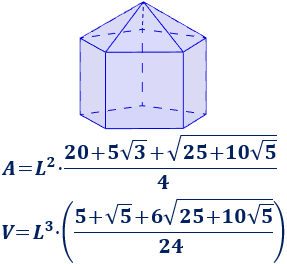
La calculadora aproxima el resultado con \(n\) decimales.
Calculadora del área y volumen:
Lado: \(L =\)
Decimales: \(n =\)
2. Definición del J9
La pirámide pentagonal elongada o sólido de Johnson J9 es el sólido geométrico obtenido al elongar una pirámide con base pentagonal adosando un prisma pentagonal a su base:
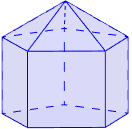
Otras perspectivas del J9:
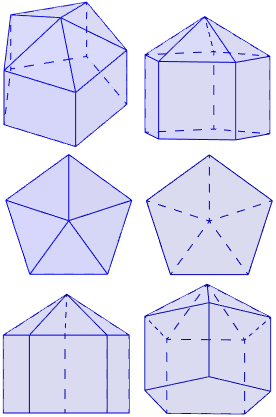
Todas las caras del J9 son polígonos regulares de igual lado: \(5\) triángulos (caras de la pirámide), \(5\) cuadrados (caras del prisma) y \(1\) pentágono (base del prisma).
El J9 tiene \(11\) caras, \(20\) aristas y \(11\) vértices.
Nota: todas las aristas del J9 tienen la misma longitud.
3. Altura del J9
Consideremos el sólido de Johnson J9 de lado \(L\).
Como todas las aristas de la pirámide miden \(L\), por lo visto en pirámide pentagonal, la altura de la pirámide es
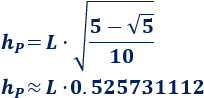
Lógicamente, la altura del prisma es \(L\), así que la altura del J9 es
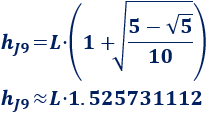
4. Fórmula del área
Desarrollo plano del sólido de Johnson J9 de lado \(L\):
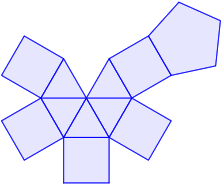
El sólido está compuesto por \(5\) triángulos equiláteros, \(5\) cuadrados y un pentágono, todos ellos de lado \(L\).
El área total de los triángulos equiláteros es
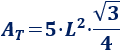
El área total de los cuadrados es
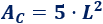
El área del pentágono regular es
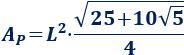
Luego el área del J9 es
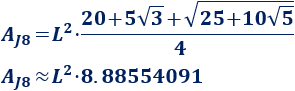
5. Fórmula del volumen
Por lo visto en pirámide pentagonal, el volumen de una pirámide pentagonal cuyas aristas miden \(L\) es
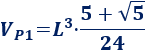
El volumen del prisma pentagonal de lado \(L\) es
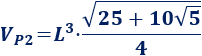
Por tanto, el volumen del J9 es
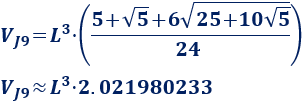
Otras calculadoras:
- Área y perímetro del círculo
- Área y perímetro del rectángulo
- Área y perímetro del rombo
- Área y perímetro del pentágono
- Área y perímetro del hexágono
- Área y perímetro del heptágono
- Área y perímetro del octágono
- Área y perímetro del eneágono
- Área y perímetro del decágono
- Área y perímetro del endecágono
- Área y perímetro del dodecágono
- Área y volumen del cono
- Área y volumen de la esfera
- Área y volumen del cilindro
- Área y volumen del tronco de cono
- Área y volumen del prisma triangular
- Área y volumen del prisma pentagonal
- Área y volumen del prisma hexagonal
- Área y volumen del prisma heptagonal
- Área y volumen del casquete esférico
- Sólido de Johnson J₁
- Sólido de Johnson J₂
- Sólido de Johnson J₃
- Sólido de Johnson J₄
- Sólido de Johnson J₅
- Sólido de Johnson J₇
- Sólido de Johnson J₈