Ecuaciones de primer grado resueltas

En esta página vamos a resolver ecuaciones de primer grado paso a paso. Comenzaremos con ecuaciones muy simples e iremos aumentando su dificultad. En las ecuaciones tendremos sumas, restas, productos y cocientes de monomios sin parte literal (es decir, números) y de monomios con la parte literal \(x\) (como \(2x\) ó \(\frac{3x}{2}\)).

Resolver una ecuación consiste en encontrar el valor que debe tomar la incógnita \(x\) para que se cumpla la igualdad. Podemos comprobar si la solución encontrada es correcta sustituyendo la incógnita \(x\) por la solución. Como regla general, una ecuación de primer grado tiene una única solución. No obstante, puede darse el caso de que no exista ninguna o que existan infinitas (veremos algún ejemplo de estos casos).

Enlace: Ejercicios interactivos de álgebra básica

Ecuación 1

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

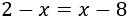
Resolvemos:

Para resolver la ecuación, debemos pasar los monomios que tienen la incógnita a una lado de la igualdad y los que no tienen la incógnita al otro lado.

Como 8 está restando en la derecha, pasa sumando al lado izquierdo:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

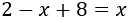
Como \(x\) está restando en la izquierda, pasa restando a la derecha:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

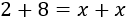
Ahora que ya tenemos separados los monomios con y sin la incógnita, podemos sumarlos. En la izquierda, sumamos \(2+8\) y, en la derecha, \(x+x\):

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

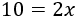
Para ver con claridad el paso siguiente, escribimos \(2x\) como un producto:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

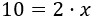
Para terminar, debemos pasar el coeficiente de la incógnita (el número 2 que multiplica a \(x\)) al lado izquierdo. Como el número 2 está multiplicando, pasa dividiendo:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

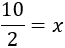
Simplificando la fracción,

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

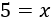
Por tanto, la solución de la ecuación es \(x = 5\).

Para comprobar la solución, sustituimos \(x\) por 5 en la ecuación para confirmar que se verifica:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

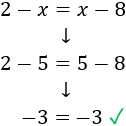
Como hemos obtenido una igualdad verdadera (-3 es igual a -3), la solución es correcta. Si, por el contrario obtenemos una igualdad falsa, significa que hemos cometido algún error en la resolución de la ecuación.

Ecuación 2

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

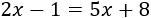
Resolvemos:

Escribimos los monomios con incógnita en la izquierda y los que no tienen incógnita en la derecha.

Como \(5x\) está sumando en la derecha, pasa restando a la izquierda. El número 1 de la izquierda está restando, así que pasa sumando al otro lado:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

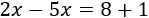
Sumamos los monomios en cada lado:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

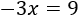
Es decir,

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

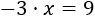
Para despejar la incógnita, debemos pasar el coeficiente de la incógnita a la derecha. Como está multiplicando, pasa dividiendo (con el signo negativo incluido):

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

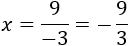
Finalmente, simplificamos la fracción:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

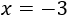
Por tanto, la solución es \(x = -3\).

Comprobamos la solución sustituyendo en la ecuación:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

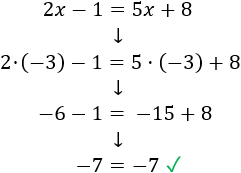
Ecuación 3

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

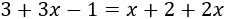
Resolvemos:

Escribimos en la izquierda los términos que tienen la incógnita y en la derecha los que no la tienen:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

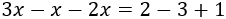
Simplificamos ambos lados:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

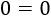
Hemos obtenido una obviedad. Esto significa que la incógnita puede tomar cualquier valor. Por tanto, todos los números reales son solución de la ecuación:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

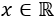
Comprobamos que la ecuación se cumple para cualquier número. Sustituimos, por ejemplo, \(x = 1\) en la ecuación:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

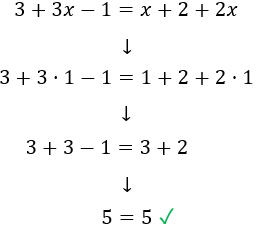
Nota: hemos comprobado para \(x = 1\), pero cualquier número cumple la ecuación. Obviamente, no podemos comprobar todos los números reales.

Ecuación 4

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

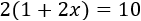
Resolvemos:

En esta ecuación tenemos un paréntesis. Un paréntesis sirve para representar que una misma operación se aplica a un grupo de monomios. El número que está delante del paréntesis está multiplicándolo, así que podemos escribir la ecuación como

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

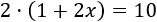
En la ecuación, el paréntesis nos dice que debemos multiplicar los monomios 1 y \(2x\) por 2.

Por tanto, podemos eliminar el paréntesis escribiendo su significado:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

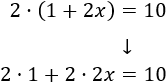
Calculamos los productos:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

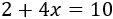
Finalmente, resolvemos la ecuación anterior:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

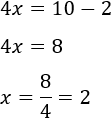
Por tanto, la solución de la ecuación es \(x = 2\).

Comprobamos la solución sustituyendo \(x = 2\) en la ecuación:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

Ecuación 5

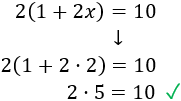
$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

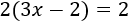
Resolvemos:

Eliminamos el paréntesis del mismo modo que hicimos en la Ecuación 4, pero no debemos olvidar que uno de los sumandos del paréntesis tiene signo negativo:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

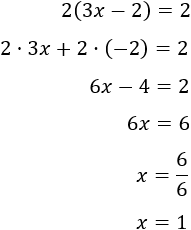
Comprobamos la solución sustituyendo \(x = 1\) en la ecuación:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

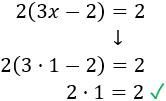
Ecuación 6

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

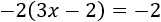
Resolvemos:

Eliminamos el paréntesis al igual que hicimos en la Ecuación 5, pero debemos tener en cuenta que el signo del número que multiplica al paréntesis es negativo:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

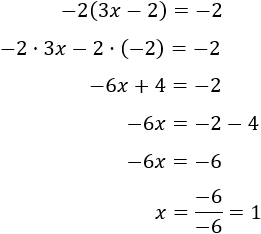
Recordad que el cociente de dos número negativos es un número positivo.

Comprobamos la solución sustituyendo \(x = 1\) en la ecuación:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

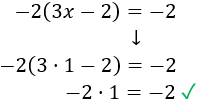
Enlace: Más ecuaciones con paréntesis.

Ecuación 7

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

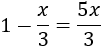
Resolvemos:

Generalmente, es mucho más rápido resolver ecuaciones sin fracciones. Como siempre podemos multiplicar una ecuación por un número distinto de 0, la multiplicamos por 3:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

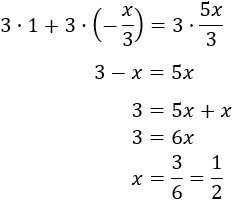
Hemos multiplicado por 3 porque es el denominador de las dos fracciones y, por tanto, se anulan los denominadores.

Comprobamos la solución sustituyendo \(x = 1/2\) en la ecuación:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

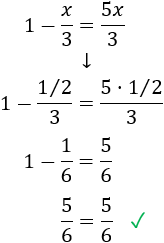
Ecuación 8

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

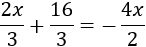
Resolvemos:

Si multiplicamos por 3 la ecuación, desaparecen las fracciones cuyo denominador es 3. Pero quedará la fracción cuyo denominador es 2. Para eliminar los denominadores de un solo paso, multiplicamos la ecuación por el mínimo común múltiplo de los denominadores.

El mínimo común múltiplo de 2 y 3 es 6. Por tanto, multiplicamos por 6 la ecuación:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

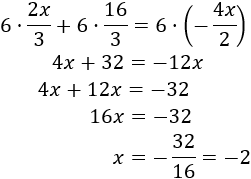
Comprobamos la solución sustituyendo \(x = -2\) en la ecuación:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

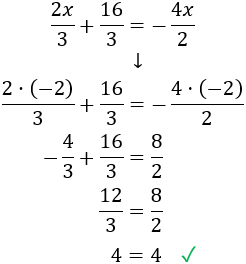
Enlace: Más ecuaciones con fracciones.

Ecuación 9

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

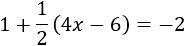
Resolvemos:

En esta ecuación tenemos una fracción, pero está multiplicando al paréntesis. Podemos multiplicar toda la ecuación por su denominador o bien operar con ella. Nosotros escogemos la segunda opción por variar de procedimiento.

Eliminamos el paréntesis multiplicando sus sumandos por el coeficiente 1/2:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

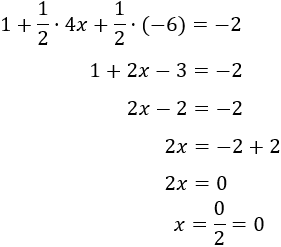
La solución de la ecuación es 0.

Comprobamos la solución sustituyendo \(x = 0\) en la ecuación:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

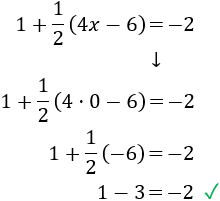
Ecuación 10

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

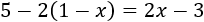
Resolvemos:

Eliminamos el paréntesis:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

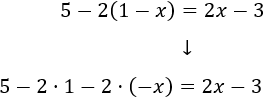
Calculamos los productos y resolvemos la ecuación. Recordad que debemos aplicar la regla de los signos:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

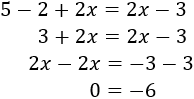
Hemos obtenido una igualdad falsa. Esto significa que no existe ningún valor para \(x\) que haga que la ecuación se cumpla. Por tanto, la ecuación no tiene ninguna solución.

Enlace: Más ecuaciones con fracciones y con paréntesis.

Ecuación 11

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

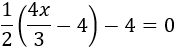
Resolvemos:

Multiplicamos toda la ecuación por 2 para eliminar la fracción de la izquierda:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

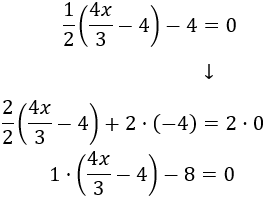
Como el paréntesis está multiplicado por 1, es como si no estuviera:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

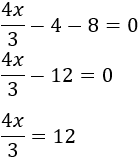
Hemos visto en ecuaciones anteriores que el coeficiente que multiplica a la incógnita pasa al otro lado dividiendo. En esta ecuación tenemos, además, un denominador. Como 3 está dividiendo a la incógnita, pasa multiplicando:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

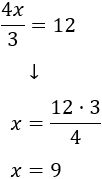
Ecuación 12

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

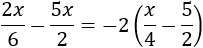
Resolvemos:

Primero que nada, podemos multiplicar el -2 del paréntesis para eliminar una de las fracciones:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

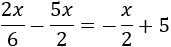
De este modo, el lugar de tres denominadores distintos, tenemos solo dos (6 y 2) y su mínimo común múltiplo es 6.

Multiplicamos toda la ecuación por 6 y resolvemos la ecuación:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

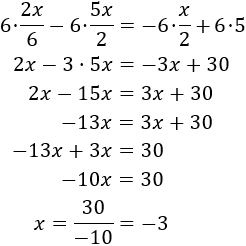
Ecuación 13

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

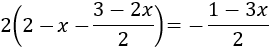
Resolvemos:

Podemos pasar el denominador del lado derecho multiplicando al lado izquierdo:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

Multiplicamos por 4 el paréntesis de la izquierda y por -1 el de la derecha:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

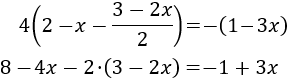
Observad que tenemos que escribir el numerador entre paréntesis al eliminar el denominador.

Continuamos resolviendo la ecuación:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

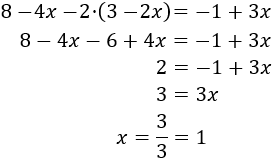
Ecuación 14

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

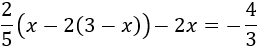
Resolvemos:

Eliminamos el paréntesis de dentro multiplicando por -2:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

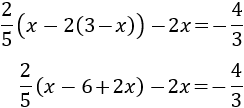
Multiplicamos la ecuación por el mínimo común múltiplo de los denominadores (3 y 5), es decir, por 15:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

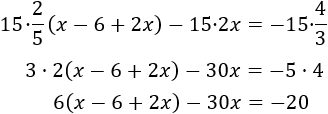
Eliminamos el paréntesis que queda y resolvemos la ecuación:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

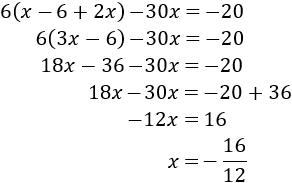
Podemos simplificar la fracción dividiendo numerador y denominador entre su máximo común divisor, es decir, 4:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

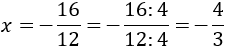
Ecuación 15

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

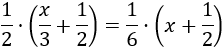
Resolvemos:

Podemos pasar el denominador 6 multiplicando al otro lado:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

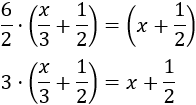
Eliminamos el paréntesis que queda multiplicando por 3:

$Ecuaciones de primer grado resueltas para secundaria. Ecuaciones simples, con fracciones, con parentesis, con signos negativos, sin solucion, con infinitas soluciones, etc. ESO.$

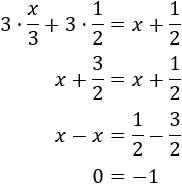
Hemos obtenido la falsa igualdad 0 = -1, independientemente del valor que tome \(x\). Esto significa que esta ecuación no tiene solución porque sea cual sea el valor de \(x\) se obtiene una igualdad falsa.

Por tanto, la ecuación no tiene ninguna solución.

Más ecuaciones:

25 ecuaciones resueltas (matesfacil.com)
83 ecuaciones explicadas (ecuacionesresueltas.com)

Problemas y Ecuaciones ©

Primeras ecuaciones

Número de soluciones

Ecuaciones con paréntesis

Ecuaciones con fracciones

Ecuaciones con fracciones y paréntesis

25 ecuaciones explicadas

Problemas con ecuaciones

Problemas de sistemas

Ecuaciones de segundo grado

Ecuaciones exponenciales

Fracción equivalente e irreductible

Problemas de Pitágoras

Calculadora de porcentajes

Calculadora de Pitágoras