Ecuaciones de segundo grado
$$ ax^2 + bx + c = 0$$
En esta página resolvemos 15 problemas sobre ecuaciones de segundo grado. En la mayoría de los problemas se pide calcular las soluciones de las ecuaciones. Las últimas 4 ecuaciones tienen soluciones complejas.
Forma general y discriminante
La forma general de una ecuación de segundo grado es:
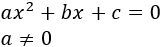
Es importante que el coeficiente \(a\) no sea 0, porque en tal caso, ya no sería una ecuación de segundo grado.
Se llama discriminante de la ecuación a
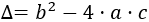
El signo de \(\Delta\) nos permite conocer el tipo de soluciones de la ecuación:
-
Si \(\Delta > 0\), hay dos soluciones reales distintas.
-
Si \(\Delta = 0\), hay una única solución real.
-
Si \(\Delta < 0\), no hay soluciones reales (hay dos soluciones complejas distintas).
Ejemplos de ecuaciones de segundo grado:
- \(x^2 -2x + 1 = 0\) tiene solo una solución real. Su discriminante es \(\Delta = 0\).
- \(x^2 - 1 = 0\) tiene dos soluciones reales distintas. Su discriminante es \(\Delta = 4 > 0\).
- \(x^2 + x + 1 = 0\) no tiene soluciones reales, tiene dos soluciones complejas. Su discriminante es \(\Delta = -3 < 0\).
Tipos de ecuaciones
Por comodidad, resolveremos la ecuación de tres formas distintas según los valores de los coeficientes \(b\) y \(c\).
Caso 1
Si \(b\), \(c\neq 0\), se dice que la ecuación es completa y sus soluciones las proporciona la fórmula
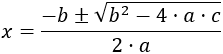
En los siguientes casos, las ecuaciones se dice que son incompletas:
Caso 2
Si \(b = 0\), la ecuación es de la forma
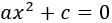
Despejando \(x^2\) y tomando raíces, las soluciones son
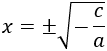
Caso 3
Si \(c = 0\), la ecuación es de la forma
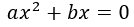
Para calcular las soluciones, extraemos el factor común \(x\):
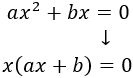
Como una multiplicación es 0 si alguno de sus factores es 0, las soluciones son
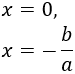
Caso 4
Si \(b = c = 0\), la ecuación es de la forma
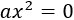
La única solución es
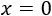
Las soluciones reales (o solución), si las hay, de la ecuación de segundo grado \(ax^2 + bx + c = 0\) son las ordenadas (primera coordenada) de los puntos de corte de la función parábola \(y = ax^2 + bx + c \) con el eje X.
Problemas resueltos
Problema 1 
Determinar el tipo y número de soluciones de la ecuación

Resolvemos:
Es una ecuación de segundo grado completa.
La fórmula del discriminante es
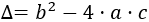
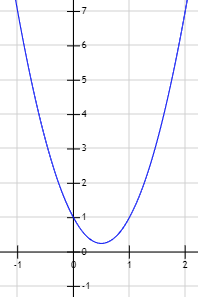
Como los coeficientes son \(a = 3\), \(b=-5\) y \(c=1\), el discriminante es
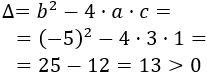
El discriminante es positivo, así que la ecuación tiene dos soluciones reales distintas.
No hemos calculado las soluciones porque no se pide en el problema, pero son
$$ x_1 = \frac{5}{6} - \frac{\sqrt{13}}{6}$$
$$ x_2 = \frac{5}{6} + \frac{\sqrt{13}}{6}$$
Gráfica de la función \(y = 3x^2 - 5x + 1\):
Observad que, como hay dos soluciones reales, hay dos puntos de corte con el eje X.
Problema 2 
Determinar el tipo y número de soluciones de la ecuación
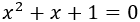
Resolvemos:
Es una ecuación completa.
La fórmula del discriminante es
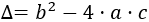
Como los coeficientes son \(a = 1\), \(b=1\) y \(c=1\), el discriminante es
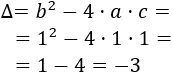
El discriminante es negativo, así que la ecuación no tiene soluciones reales. Tiene dos soluciones complejas distintas:
$$ x_1 = -\frac{1}{2} - i\cdot \frac{\sqrt{3}}{2}$$
$$ x_2 = -\frac{1}{2} + i\cdot \frac{\sqrt{3}}{2}$$
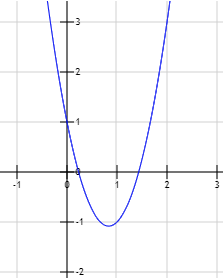
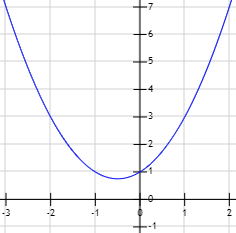
Gráfica de la función \(y = x^2 + x + 1\):
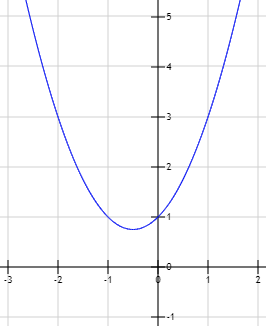
Observad que, como no hay soluciones reales, no hay puntos de corte con el eje X.
Problema 3 
Determinar el tipo y número de soluciones de la ecuación
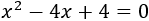
Resolvemos:
Es una ecuación completa.
La fórmula del discriminante es
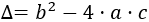
Como los coeficientes son \(a = 1\), \(b=-4\) y \(c=4\), el discriminante es
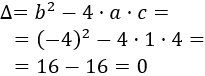
El discriminante es nulo, así que la ecuación tiene una única solución real.
La solución es \(x = 2\).
Gráfica de la función \(y = x^2 -4x +4\):
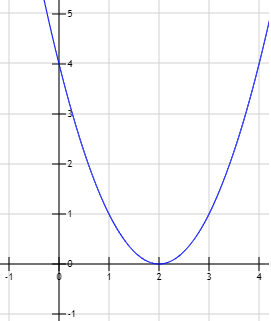
Como solo hay una solución real, sólo hay un punto de corte con el eje X y, además, coincide con el vértice de la parábola.
Problema 4 
Resolver la ecuación de segundo grado incompleta
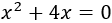
Resolvemos:
Es una ecuación incompleta porque \(c=0\). Extraemos el factor común \(x\) para calcular las soluciones:
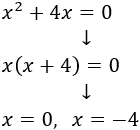
La ecuación tiene dos soluciones reales distintas: \( x_1=0\) y \(x_2= -4\).
Observad que el discriminante es 0: \(\Delta = 4^2 -4\cdot 4\).
Gráfica de la función \(y = x^2 + 4x \):
Observad que la primera coordenada de los puntos de corte con el eje X son las soluciones de la ecuación.
Problema 5 
Encontrar las raíces de la función polinómica de segundo grado
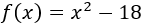
Resolvemos:
Las raíces del polinomio \(f\) son los valores de \(x\) para los que \(f(x)\) es 0, es decir, son las soluciones de la ecuación
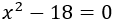
La ecuación es incompleta y la podemos resolver rápidamente tomando raíces cuadradas:
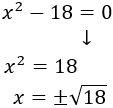
Simplificamos:
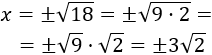
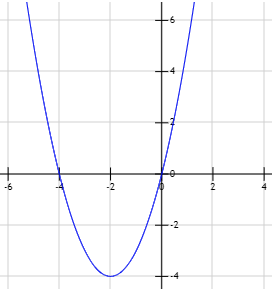
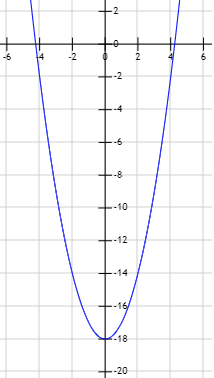
La ecuación tiene dos soluciones reales distintas y son las raíces de la función polinómica: \( x_1= 3\sqrt{2}\) y \(x_2=-3\sqrt{2}\).
Gráfica de la función \(f(x) = x^2 -18 \):
Problema 6 
Resolver la siguiente ecuación de segundo grado completa y escribirla en forma factorizada:
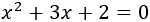
Resolvemos:
Es una ecuación completa con coeficientes \(a = 1\), \(b = 3\) y \(c=2\).
Aplicamos la fórmula para calcular las soluciones:
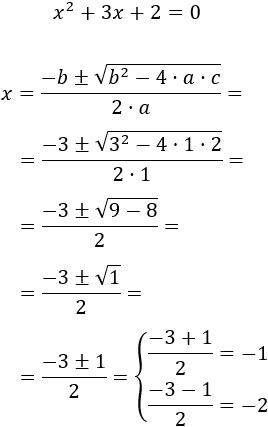
Por tanto, las soluciones son \(x_1 =-1\) y \(x_2 = -2\).
Si \(x_1\) y \(x_2\) son las soluciones de la ecuación \(ax^2 + bx + c = 0\), entonces su forma factorizada es
$$ a\cdot (x-x_1)\cdot (x - x_2) = 0 $$
Si solo tiene una solución \(x_1\), entonces es
$$ a\cdot (x-x_1)^2 = 0 $$
Factorizamos la ecuación del problema:
$$ x^2 + 3x + 2 = (x+1)(x+2) = 0$$
Gráfica de la función \(y = x^2 +3x + 2\):
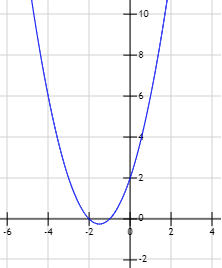
Problema 7 
Resolver y factorizar la ecuación
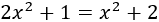
Resolvemos:
Tenemos una ecuación de segundo grado, pero no se encuentra en su forma general \(ax^2 + bx + c = 0\). Es fácil conseguir dicha forma operando un poco:
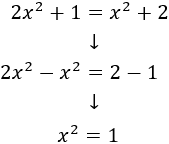
La forma general es, pues, \(x^2 -1 =0\).
Es una ecuación incompleta. Para resolverla, calculamos la raíz cuadrada:
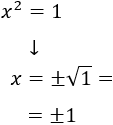
Las soluciones son \(x_1 = 1\) y \(x_2=-1\).
Factorizamos la ecuación:
$$ x^2 - 1 = (x+1)(x-1)$$
Gráfica de la función \(y = x^2 -1\):
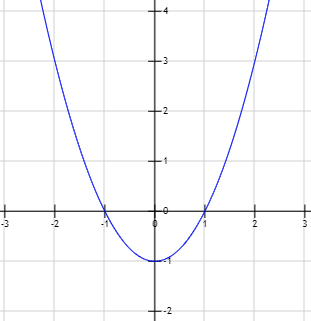
Problema 8 
Resolver la ecuación completa
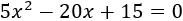
Resolvemos:
Es una ecuación completa con coeficientes \(a = 5\), \(b = -20\) y \(c=15\).
Aplicamos la fórmula para calcular las soluciones:
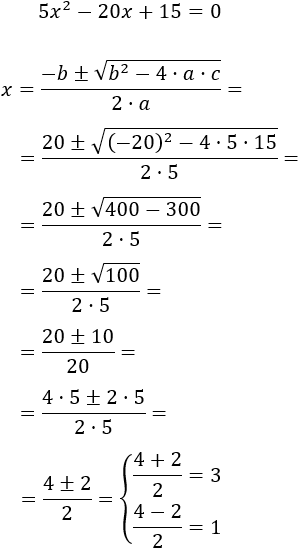
Las soluciones de la ecuación son \(x_1 = 3\) y \(x_2= 1 \).
Gráfica de la función \(y = 5x^2 - 20x + 15\):
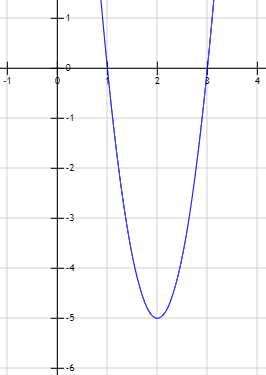
Problema 9 
Factorizar el polinomio
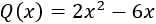
Deducir las raíces del polinomio a partir de la factorización.
Resolvemos:
Normalmente, para factorizar, igualamos a 0 el polinomio y buscamos las soluciones. Sin embargo, este polinomio es muy sencillo de factorizar porque podemos extraer factor común de 2 y de \(x\):
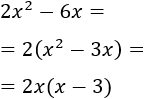
La factorización es \(Q(x) = 2x(x-3)\).
Las raíces de \(Q(x)\) son los valres de \(x\) para los que \(Q(x)=0\). Es decir, son las soluciones de la ecuación
$$ 2x(x-3) = 0 $$
Un producto de dos factores es 0 cuando alguno de los factores es 0. Por tanto, las raíces del polinomio son \(x=0\) y \(x = 3\).
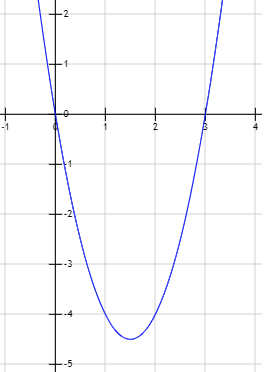
Gráfica de la función \(Q(x) = 2x^2 - 6x \):
Problema 10 
Encontrar las raíces del polinomio
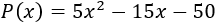
Resolvemos:
Para encontrar las raíces, igualamos el polinomio a 0:
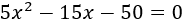
Tenemos una ecuación completa con coeficientes \(a = 5\), \(b = -15\) y \(c=-50\).
Aplicamos la fórmula:
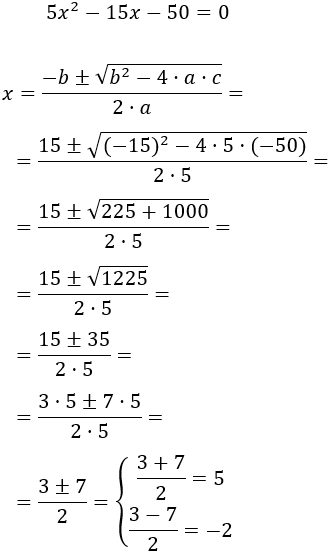
Las raíces del polinomio son \(x_1 = -2\) y \(x_2=5\).
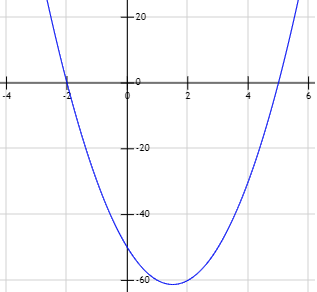
Gráfica de la función \(y = 5x^2 - 15x - 50\):
Problema 11 
Resolver la ecuación de segundo grado completa
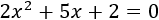
Resolvemos:
Es una ecuación completa con coeficientes \(a = 2\), \(b = 5\) y \(c=2\).
Aplicamos la fórmula:
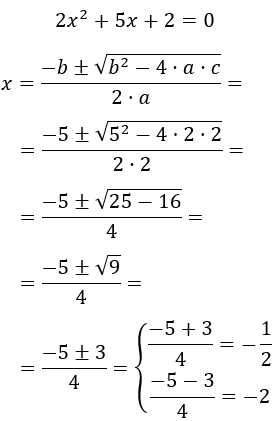
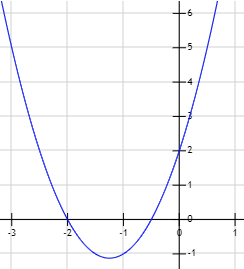
Las soluciones de la ecuación son \(x_1 = -1/2\) y \(x_2 = -2\).
Gráfica de la función \(y = 2x^2 + 5x + 2\):
Problema 12 
Resolver la ecuación
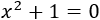
Resolvemos:
Es una ecuación incompleta y no tiene soluciones reales porque su discriminante es \(\Delta = -4 < 0\).
Despejamos \(x\) para calcular las soluciones tomando raíces y teniendo en cuenta que la unidad imaginaria es \( i = \sqrt{-1}\):

Las soluciones de la ecuación son imaginarias: \(x_1 = i\) y \(x_2 = -i\).
Gráfica de la función \(y = x^2 + 1\):
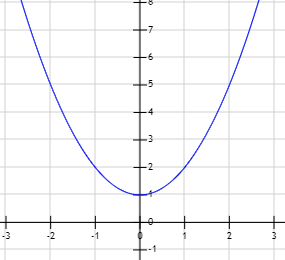
Al no tener soluciones reales, la parábola no corta el eje X.
Problema 13 
Resolver la ecuación
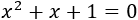
Resolvemos:
Es una ecuación completa con coeficientes \(a = 1\), \(b = 1\) y \(c=1\).
El discriminante de la ecuación es \(\Delta = -3 < 0\), así que no tiene soluciones reales.
Como la ecuación es completa, aplicamos la fórmula para calcular las soluciones complejas:
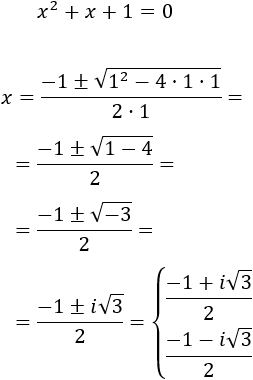
Gráfica de la función \(y = x^2 + x + 1\):
Problema 14 
Resolver la ecuación
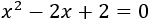
Resolvemos:
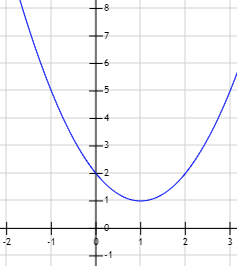
Es una ecuación completa con coeficientes \(a = 1\), \(b = -2\) y \(c=2\) y su discriminante es \(\Delta = 2^2 -4·2 = -4\), así que no tiene soluciones reales.
Aplicamos la fórmula para calcular las soluciones complejas:
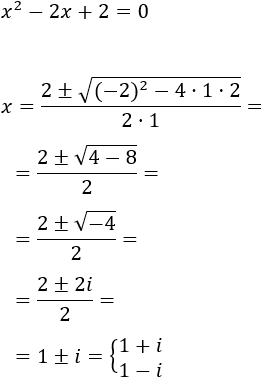
Las soluciones de la ecuación son \(1\pm i\).
Gráfica de la función \(y = x^2 - 2x + 2\):
Problema 15 
Resolver la ecuación
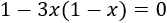
Resolvemos:
Antes que nada, operamos en la ecuación para obtener su forma general:
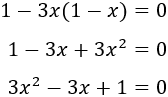
Es una ecuación completa con coeficientes \(a = 3\), \(b = -3\) y \(c=1\) y su discriminante es \(\Delta = -3\), por lo que no tiene soluciones reales.
Aplicamos la fórmula:
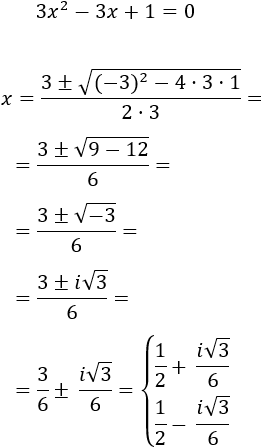
Gráfica de la función \(y = 3x^2 - 3x + 1\):