Ecuaciones de primer grado: problemas resueltos
En esta página resolvemos 20 problemas con la ayuda de ecuaciones de primer grado. La finalidad de este tema es aprender a traducir un problema en una ecuación. Asumimos que ya sabemos resolver ecuaciones de primer grado.
Problema 1 
Encontrar el número que cumple que la suma de su doble y de su triple es igual a 100.
Solución:
Si llamamos \(x\) al número que buscamos, entonces
- su doble es \(2\cdot x\)
- y su triple es \(3\cdot x\).
Como la suma de los dos últimos números debe ser 100, tenemos la ecuación
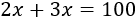
Resolvemos la ecuación:
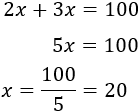
El número buscado es \(x = 20\).
Comprobamos la solución
En efecto, el doble de 20 es 40, su triple es 60 y ambos números suman 100:
$$ 40 + 60 = 100$$
Problema 2 
Si Ana es 12 años menor que Eva y dentro de 7 años la edad de Eva es el doble que la edad de Ana, ¿qué edad tiene Eva?
Solución:
Supongamos que \(x\) es la edad de Ana. Como Eva tiene 12 años más que Ana, su edad es \(x+12\).
Dentro de 7 años,
- Ana tendrá la edad actual más 7, es decir, tendrá \(x+7\).
- Del mismo modo, Eva tendrá \((x+12)+7 = x +19\).
- Y e doble de la edad de Ana será \(2\cdot (x+7)\).
Debemos resolver la ecuación
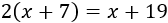
Resolvemos:
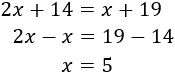
Por tanto, la edad actual de Ana es 5 y la de Eva es 17.
Comprobamos la solución
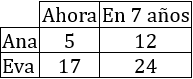
- Ana (5) tiene 12 años menos que Eva (17) ya que 5 + 12 = 17.
- Dentro de 7 años: Eva (24) tiene el doble que Ana (12) ya que 12·2 = 24.
Problema 3 
Si 25,5 es el 15% de una cierta cantidad, ¿cuál es el 80% de dicha cantidad?
Solución:
Si \(x\) es la cantidad, su 15% se calcula multiplicando \(x\) por 15 y dividiendo entre 100. Como el 15% de \(x\) es 25,5, tenemos la ecuación
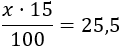
La resolvemos:
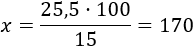
Ahora calculamos el 80% de 170 multiplicando por 80 y dividiendo entre 100:
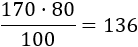
Por tanto, el 80% es 136.
Comprobamos la solución
Hemos dicho que la cantidad total es \(x = 170\). Entonces,
- El 15% de 170 es 25.5:
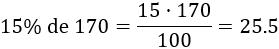
- El 80% de 170 es 136:
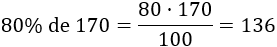
Enlace: problemas de porcentajes.
Problema 4 
Hallar el número \(x\) sabiendo que la cuarta parte de la quinta parte de la tercera parte de \(x\) es 3.
Solución:
La tercera parte de \(x\) es
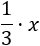
La quinta parte del número anterior es
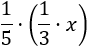
La cuarta parte del número anterior es
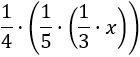
La ecuación del problema es
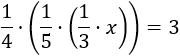
Recordad que para multiplicar las fracciones debemos multiplicar los numeradores y los denominadores:
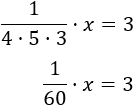
Resolvemos la ecuación:
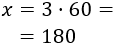
Por tanto, el número es \(x = 180\).
Comprobamos la solución
- \(x\) es 180.
- La tercera parte de 180 es 180/3 = 60.
- La quinta parte de 60 es 60/5 = 12.
- La cuarta parte de 12 es 12/4 = 3.
Problema 5 
Hallar los números positivos de tres cifras que cumplen que la primera cifra es el doble de la segunda y la tercera es el triple de la segunda.
Comprobar que la suma de sus 3 cifras es exactamente el séxtuple de su segunda cifra.
Solución:
Como la segunda y tercera cifra están escritas en función de la segunda, llamamos \(x\) a la segunda cifra.
La primera cifra es el doble de la segunda, es decir, es \(2x\).
La tercera cifra es el triple de la segunda, es decir, es \(3x\).
El número de 3 cifras que buscamos es [2x][x][3x] (los corchetes [] los usamos para separar las cifras del número).
El número \(x\) no puede ser 0 porque si no, el número buscado sería 000 = 0 y no tiene 3 cifras.
Si \(x = 1\), el número es 213.
Si \(x = 2\), el número es 426.
Si \(x = 3\), el número es 639.
El número \(x\) tampoco puede ser mayor que 3 porque si no, al calcular la tercera cifra obtendríamos un número de más de una cifra. Por ejemplo, si \(x = 4\) tendríamos [8][4][12].
Por tanto, los números de 3 cifras que cumplen las condiciones del enunciado son únicamente 213, 426 y 639.
Segunda parte
La suma de las tres cifras del número es [2x][x][3x] es
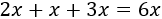
Es decir, es el séxtuple de \(x\), es decir, el séxtuple de la segunda cifra.
En efecto,
- Número 213: 2 + 1 + 3 = 6, que es igual a 6·1.
- Número 426: 4 + 2 + 6 = 12, que es igual a 6·2.
- Número 639: 6 + 3 + 9 = 18, que es igual a 6·3.
Problema 6 
Encontrar dos números positivos y consecutivos de modo que su la suma de sus dobles sea igual al triple del mayor de los dos números.
Solución:
El número consecutivo de un número es el que le sigue. Por ejemplo, 2, 3 y 4 son consecutivos. El consecutivo de un número se calcula sumándole 1. Por ejemplo, el consecutivo de 2 es 2 + 1 = 3 y el de 3 es 3 + 1 = 4.
Supongamos que \(x\) es el menor de los números que buscamos. Entonces, su consecutivo es el número que le sigue, es decir, es \(x+1\).
El doble del número menor es \(2\cdot x\) y el doble de mayor es \(2\cdot (x+1)\).
Por tanto, la suma de los dobles es
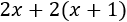
Queremos que esta suma sea igual al triple del mayor de los dos números y como \(x+1\) es el mayor de los números, la suma debe ser igual a \(3\cdot (x+1)\).
La ecuación que tenemos es
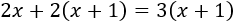
Resolvemos la ecuación:
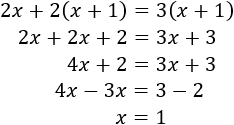
Por tanto, los números buscados son \(x = 1\) y \(x+1 = 2\).
Comprobamos la solución
En efecto, los números 1 y 2 son positivos, consecutivos y la suma de sus dobles es 2 + 4 = 6, que es el triple del mayor de ellos.
Problema 7 
Hallar el número positivo de tres cifras cuyas segunda y tercera cifra son el doble de la primera de modo que la suma de las dos primeras cifras es 9.
Solución:
Si la primera cifra es \(x\), la segunda y la tercera cifra son \(2x\).
Por tanto, el número de 3 cifras buscado es [x][2x][2x].
La suma de las dos primeras cifras es 9:
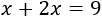
Resolvemos la ecuación:
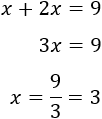
El número buscado es 366.
Comprobamos la solución
- La segunda y la tercera cifra son el doble de la primera: 2·3 = 6.
- Las dos primeras cifras suman 9: 3 + 6 = 9.
Problema 8 
El padre de Andrés tiene 30 años más que él y su madre tiene 5 años menos que su padre. Averiguar la edad de actual de Andrés sabiendo que la suma de las edades de sus padres es 7 veces la edad de Andrés.
Solución:
Si Andrés tiene \(x\) años, su padre tiene \(x+30\). Como la madre tiene 5 años menos que su padre, tiene \(x+30-5=x+25\).
La suma de las edades de los padres es 7 veces la de Andrés:
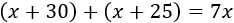
Resolvemos la ecuación:
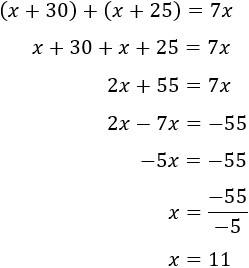
La edad de Andrés es 11 años y las edades de su padre y de su madre son 41 y 36, respectivamente.
Comprobamos la solución
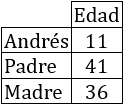
- El padre tiene 30 años más que Andrés: 11 + 30 = 41.
- La madre tiene 5 años menos que el padre: 41 - 5 = 36.
- La suma de las edades de los padres es 41 + 36 = 77, que es 7 veces la edad de Andrés: 7·11 = 77.
Problema 9 
Tanto Andrés como su hermano Jaime tienen guardado su propio dinero en sus respectivas huchas. Andrés sabe que tiene el triple de dinero que su hermano, así que decide darle 130€.
Después de la donación, Andrés se compra un libro de 15€, con lo que sus ahorros son ahora el doble que los de su hermano.
¿Cuánto dinero tenía cada uno inicialmente? ¿Y ahora?
Solución:
Si Jaime tenía \(x\) euros, entonces Andrés tenía \(3x\).
Como Andrés le da 130€ a Jaime, Andrés tiene \(3x-130\) y Jaime tiene \(x + 130\). Pero como Andrés realiza una compra de 15€, tiene \(3x-130-15 =3x-145\).
Como la cantidad actual de Andrés es el doble que la de Jaime,
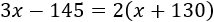
Resolvemos la ecuación:
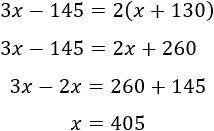
Jaime tenía 405€ y ahora tiene 535€ y Andrés tenía 1215€ y ahora tiene 1070€.
Comprobamos la solución
Comprobamos el resultado realizando todas los operaciones que se enuncian en el problema:
- Inicialmente, Andrés tenía 1215€ y Jaime tenía 405€: Andrés tenía el triple que Jaime: 405·3 = 1215€.
- Cuando Andrés le dio 130€ a Jaime: Andrés tenía 1215 - 130 = 1085€ y Jaime tenía 405 + 130 = 535€.
- Andrés compra un libro de 15€ y, por tanto, le quedan 1085 - 15 = 1070€.
- Jaime tiene 535€ y el doble de su dinero es 2·535 = 1070€, que es el dinero que tiene Andrés.
Problema 10 
Buscar un número positivo \(x\) de modo que al sumarlo con su doble se obtenga el triple de dicho número.
¿Cuántos números \(x\) cumplen lo anterior?
Solución:
El doble del número \(x\) que buscamos es \(2x\) y el triple es \(3x\). Queremos que la suma de \(x\) y de su doble \(2x\) sea exactamente \(3x\):
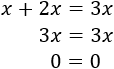
La ecuación \(x+2x=3x\) tiene infinitas soluciones. Es decir, todos los números la cumplen.
Cualquier número positivo más su doble tiene como resultado al triple de dicho número.
Comprobamos la solución
No podemos comprobar que todos los números positivos cumplen la ecuación, pero podemos hacerlo con algunos:
- Si \(x = 1\), la suma de 1 y su doble 2·1 = 2 es 3, que es el triple de 1: 3·1 = 3.
- Si \(x = 5\), la suma de 5 y su doble 2·5 = 10 es 15, que es el triple de 5: 3·5 = 15.
- Si \(x = 10\), la suma de 10 y su doble 2·10 = 20 es 30, que es el triple de 10: 3·10 = 30.
- Si \(x = 50\), la suma de 50 y su doble 2·50 = 100 es 150, que es el triple de 50: 3·50 = 150.
Problema 11 
La ecuación que proporciona la distancia recorrida, \(d\), por un vehículo que se mueve a velocidad constante \(v\) durante un tiempo \(t\) es
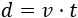
¿Cuántos minutos tarda un coche en recorrer 100 kilómetros a una velocidad de 80 km/h?
Solución:
Sustituimos la velocidad y la distancia en la ecuación del movimiento:
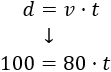
Resolvemos la ecuación:
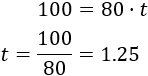
Como la velocidad es en km/h, el tiempo obtenido es en horas. Para tener el tiempo en minutos tenemos que multiplicar las horas por 60:
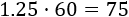
Por tanto, el coche tarda 75 minutos en recorrer 100km a 80km/h.
Problema 12 
Marisa pagó un total de 4.8€ cuando fue a comprar peras. Si el precio de cada pera era de 0.3€ y el de la bolsa de tela donde las llevaba le costó 1.5€, ¿cuántas peras compró?
Solución:
Llamamos \(x\) al número de peras que compró Marisa.
Como cada pera cuesta 0.3€, el precio de todas las peras es \(0.3\cdot x\).
El precio de la bolsa es de 1.5€.
Marisa pagó 4.8€, que es la suma del precio de las peras y la bolsa, así que tenemos la ecuación
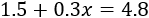
Resolvemos:
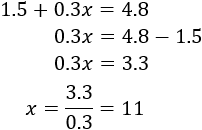
Por tanto, Marisa compró 11 peras.
Problema 13 
Carlos ha comprado en una tienda de deporte el mismo número de pelotas de tenis que de pimpón. Si las pelotas de tenis cuestan 1.2€ cada una y las de pimpón cuestan 0.3€ cada una, ¿cuántas pelotas ha comprado en total si ha pagado 9€?
Solución:
Llamamos \(x\) al número de pelotas de tenis, que también es el número de pelotas de pimpón.
El precio total pagado por las pelotas de tenis es \(1.2\cdot x\).
Igualmente, el total pagado por las de pimpón es \(0.3\cdot x\).
Sabemos que el precio de todas las pelotas es 9€, así que tenemos la ecuación
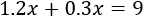
Resolvemos:
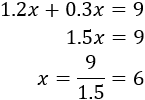
Carlos ha comprado 6 pelotas de cada. Es decir, ha comprado un total de 12 pelotas.
Problema 14 
Marcos tiene en su monedero 22.5€ en monedas de 2€ y de 0.5€ y, además, el mismo número de monedas de 2€ que de 0.5€. ¿Cuántas monedas tiene Marcos?
Solución:
Llamamos \(x\) al número de monedas de 2€, que también es el número de monedas de 0.5€.
Las monedas de 2€ suman \(2\cdot x\) euros.
Las monedas de 0.5€ suman \(0.5\cdot x\) euros.
Como todas las monedas suman 22.5 euros, tenemos la ecuación
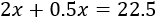
Resolvemos:
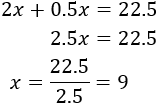
Por tanto, Marcos tiene 9 monedas de 2€ y 9 monedas de 0.5€.
Problema 15 
Tenemos un rectángulo cuya base mide el doble que su altura y cuyo perímetro es 42 centímetros. ¿Cuáles son las dimensiones del rectángulo?
Solución:
Llamamos \(x\) a la altura del triángulo.
Como la base mide el doble que la altura, ésta mide \(2\cdot x\).
El perímetro de un rectángulo se calcula sumando sus cuatro lados (dos alturas y dos bases):
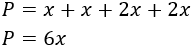
Como el perímetro es \(P = 42\), tenemos
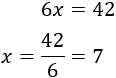
Por tanto, las dimensiones del rectángulo son 7 x 14 cm.
Problema 16 
Rosa ha comprado un total de 38 caramelos de fresa y de menta por un total de 3€. Si el precio de los caramelos de fresa es de 0.05€/u y el de los de menta es de 0.1€/u, ¿cuántos caramelos de cada sabor ha comprado Rosa?
Solución:
Llamamos \(x\) al número de caramelos de fresa.
Como el total de caramelos es 38, entonces podemos calcular el número de caramelos de menta restando el número de caramelos de fresa al total. Es decir, el número de caramelos de menta es \(38-x\).
Como cada caramelo de fresa cuesta 0.05€, el coste total de los caramelos de fresa es \(0.05\cdot x\).
Del mismo modo, como el precio de los de menta es de 0.1€/u, el coste total es \(0.1\cdot (38-x)\).
Observad que es muy importante escribir \(38-x\) entre paréntesis porque no es lo mismo multiplicar con que sin paréntesis:
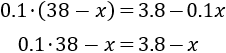
Sabemos que Rosa ha pagado un total de 3€, así que tenemos la ecuación
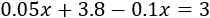
Resolvemos:
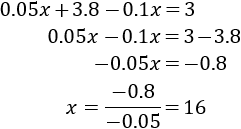
Por tanto, Rosa ha comprado 16 caramelos de fresa.
El número de caramelos de menta es 22:
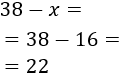
Problema 17 
Calcular la velocidad en m/s de un atleta que tarda 10 minutos en recorrer una distancia de 3 kilómetros.
Solución:
En el problema 11 vimos que la distancia recorrida por un móvil que se mueve a velocidad constante \(v\) durante un tiempo \(t\) es
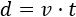
De esta ecuación conocemos la distancia (3 km) y el tiempo (10 min), así que podemos calcular la velocidad \(v\).
Como queremos que la velocidad sea en m/s, tenemos que escribir la distancia en metros y el tiempo en segundos:
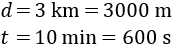
Escribimos los datos en la fórmula:
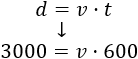
Resolvemos la ecuación:
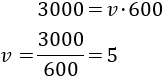
Por tanto, la velocidad del atleta es de 5 m/s.
Problema 18 
Daniel ha cortado una cuerda de 48 metros en dos trozos, de modo que uno de ellos mide el triple que el otro. ¿Cuánto mide cada trozo?
Solución:
Llamamos \(x\) a la longitud del trozo corto de cuerda.
Entonces, el trozo largo mide el triple, esto es, \(3\cdot x\).
Como la cuerda mide un total de 48 metros, tenemos la ecuación
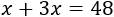
Resolvemos:
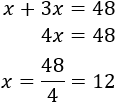
Por tanto, el trozo corto mide 12 metros y el largo mide 36 metros (porque \(3\cdot 12 = 36\)).
Problema 19 
En la factura de la compañía del agua potable pone que el coste mensual del servicio es de 13€ de mantenimiento más un coste fijo por cada litro de consumo. ¿Cuánto cuesta el litro de agua si hemos pagado 28€ en un mes con 1500 litros de consumo? ¿Cuánto pagaremos si en un mes consumismos el doble de agua?
Solución:
Llamamos \(x\) al precio del litro de agua.
Si consumimos 1500 litros, pagaremos \(1500\cdot x\) de consumo; más los 13€ de mantenimiento.
Si en total pagamos 28€, entonces tenemos la ecuación
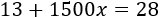
Resolvemos:
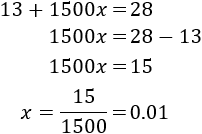
Por tanto, el precio del litro de agua es de 0.01€.
Si consumismos el doble de agua, el precio de la factura no será el doble, ya que se duplica el precio del consumo, pero no el del mantenimiento.
La cantidad de litros serán 3000, a un precio de 0.01€/L más 13€ de mantenimiento. En total, serán 43 euros ya que
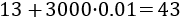
Problema 20 
- Un número más su tercera parte es 24. ¿Qué número es?
- El doble y el triple de un número suman 35. ¿Qué número es?
- La mitad y la tercera parte de un número suman 25. ¿Qué número es?
Solución:
En cada uno de los tres casos, llamamos \(x\) al número buscado.
Primer apartado
Como la tercera parte de \(x\) es \(x/3\), tenemos la ecuación
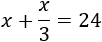
Resolvemos:
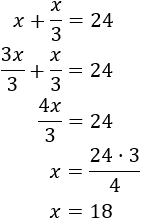
Segundo apartado
Como el doble y el triple de \(x\) son \(2x\) y \(3x\), tenemos la ecuación
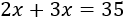
Resolvemos:
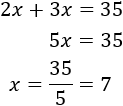
Tercer apartado
Como la mitad y la tercera parte de \(x\) son \(x/2\) y \(x/3\), tenemos la ecuación
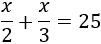
Resolvemos:
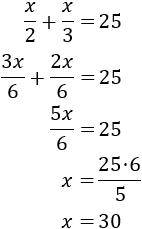
Más problemas similares:
- 45 Problemas de ecuaciones (matesfacil.com)
- 32 Problemas de edades (matesfacil.com)
- 50 Problemas de ecuaciones (ecuacionesresueltas.com)