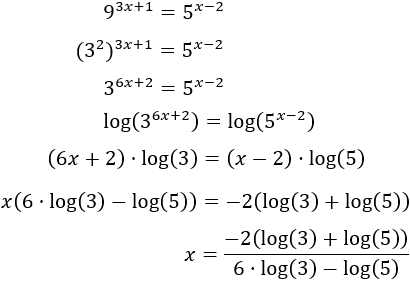Ecuaciones exponenciales
En esta página explicamos y resolvemos unas 15 ecuaciones exponenciales cada vez más complejas. Las primeras ecuaciones que trabajamos son las que se resuelven fácilmente igualando exponentes, las siguientes son las que precisan un cambio de variable y las últimas son las que se resuelven por logaritmos. También, veremos cómo resolver una ecuación exponencial con raíces.
Es imprescindible conocer las propiedades de las potencias ya que nos permiten simplificar las ecuaciones. Generalmente, escribiremos los números enteros de las ecuaciones en su forma de potencia.
Índice de contenidos:
- Ecuación básica
- Cambio de variable
- Ecuación exponencial con raíces
- Soluciones logarítmicas
Ecuación básica
La ecuación por la que empezamos es una igualdad entre una exponencial y un número entero que puede escribirse como una potencia con la misma base que la exponencial.
Por ejemplo, la ecuación \(5^x = 125\) puede escribirse como
$$ 5^x = 5^3 $$
Teniendo en cuenta que dos potencias con la misma base son iguales si, y solamente si, sus exponentes son iguales, la solución de la ecuación \(5^x=5^3\) es \(x = 3\).
Ecuación 1
Resolver la ecuación igualando exponentes de potencias con base común:
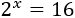
Solución:
Es fácil ver que la solución de la ecuación es \(x = 4\) porque \(2^4 = 16\). No obstante, por ser metódicos, lo que tenemos que hacer es escribir 16 como la potencia \(2^4\):
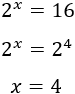
Hemos igualado los exponentes de las potencias porque el resultado de \(2^x\) es igual a \(2^4\) si, y sólo si, \(x = 4\).
A veces, también tendremos que escribir las bases de las exponenciales como potencias. Por ejemplo,
Ecuación 2
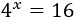
Solución:
Escribimos 16 como la potencia \( 2^4\) y la base de la exponencial \(4^x\) como \(4 = 2^2\) para tener bases comunes:
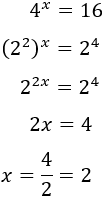
También, podríamos simplemente haber escrito 16 como \(4^2\) y directamente tendríamos \(x = 2\). No obstante, siempre es preferible usar número primos.
Si tenemos números, potencias o exponenciales que multiplican a las exponenciales, podemos simplificarlas aplicando las propiedades de las potencias.
Por ejemplo,
-
Si tenemos \(2\cdot 2^x\), eliminamos el 2 de la izquierda escribiendo +1 en el exponente:
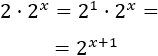
-
Si tenemos \(4\cdot 2^x\), eliminamos el 4 de la izquierda escribiendo +2 en el exponente:
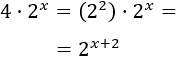
Ecuación 3
Resolver la ecuación escribiendo potencias cuyas bases sean iguales y números primos:
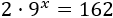
Solución:
Reescribimos la exponencial \(9^x = (3^2)^x\) y pasamos el 2 dividiendo al otro lado:
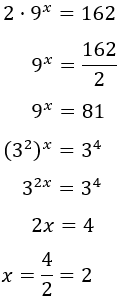
Ecuación 4
Resolver siguiendo los ejemplos anteriores:
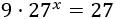
Solución:
Escribimos 9 y 27 como potencias de 3 y resolvemos:
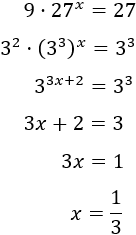
Ecuación 5
Resolver siguiendo los ejemplos anteriores:
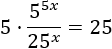
Solución:
Escribimos 5 y 25 como potencias de base 5:
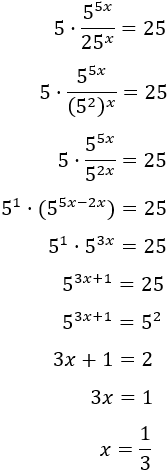
A veces, haremos el paso inverso: escribir las exponenciales como un producto.
Ecuación 6
Resolver la ecuación escribiendo la exponencial como un producto:
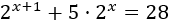
Solución:
Escribimos la exponencial como un producto:
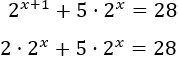
Podemos extraer factor común de \(2^x\):
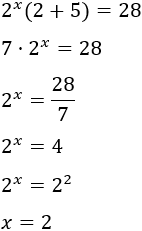
Cambio de variable
Cuando en los exponentes tenemos coeficientes en la incógnita, podemos aplicar un cambio de variable. Normalmente, será suficiente un cambio como \(2^x=t\) ó \(3^x = t\) (la base dependerá de las exponenciales de la ecuación).
Ecuación 7
Resolver la siguiente ecuación aplicando el cambio de variable \(2^x = t\):
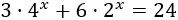
Solución:
Lo primero que hacemos es escribir la base de la exponencial \(4^x\) como la potencia \(2^2\), así tendremos dos exponenciales con la misma base:
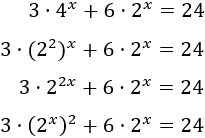
Ahora, aplicamos el cambio de variable \(2^x = t\), con lo que obtenemos una ecuación de segundo grado:
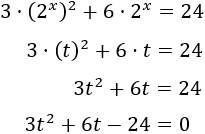
Las soluciones de la ecuación de segundo grado son
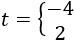
Finalmente, deshacemos el cambio de variable: como \(t=2^x\), tenemos
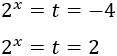
La primera ecuación, \(2^x = -4\) no tiene solución real (porque la potencia de un número positivo no puede ser negativa).
De la segunda ecuación ,tenemos que \(x = 1\). Por tanto, la solución (real) de la ecuación es \(x = 1\).
Ecuación 8
Resolver mediante el cambio de variable \(t = 3^x\):
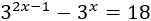
Solución:
Escribimos la exponencial \(3^{2x-1}\) como una potencia de 3 por una exponencial al cuadrado y aplicamos el cambio de variable \(t = 3^x\):
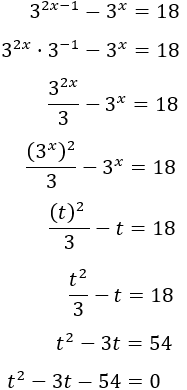
Las soluciones de la ecuación de segundo grado son
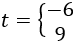
Como \(t=3^x\), tenemos
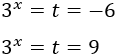
La primera ecuación, \(3^x = -6\) no tiene solución real. De la segunda ecuación tenemos que \(x = 2\).
Ecuación 9
Resolver mediante el cambio de variable \(t=7^{-x}\):
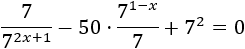
Solución:
Simplificamos un poco la ecuación:
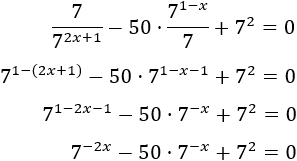
Tenemos que aplicar un cambio de variable, pero como las exponenciales tienen el exponente negativo, aplicamos el cambio \( t = 7^{-x}\):
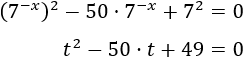
Resolvemos la ecuación de segundo grado:
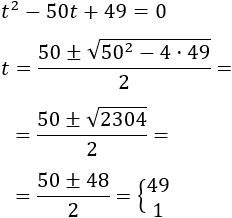
Como \(t = 7^{-x}\), tenemos
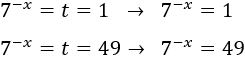
De la primera ecuación tenemos que \(x = 0\). Resolvemos la segunda:
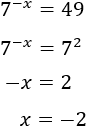
Por tanto, la ecuación exponencial tiene dos soluciones: \(x = 0\) y \(x = -2\).
Ecuación 10
Resolver mediante un cambio de variable:
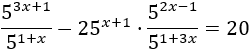
Solución:
Operamos en la ecuación para simplificarla:
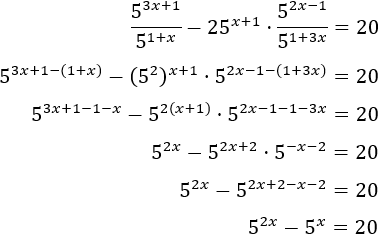
Aplicamos el cambio de variable \(5^x = t\):
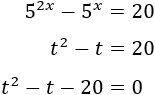
Resolvemos la ecuación de segundo grado:
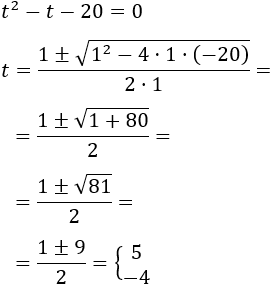
Como \(t = 5^x\), hemos obtenido que
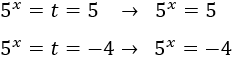
De la primera ecuación tenemos la solución \(x = 1\). La segunda ecuación no tiene solución real.
Ecuación 11
Resolver mediante un cambio de variable:
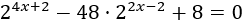
Solución:
Simplificamos las exponenciales para aplicar un cambio de variable:
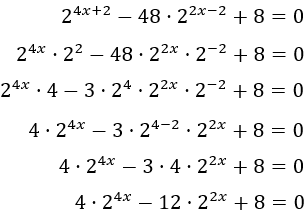
En lugar de \(t = 2^{x}\), aplicamos el cambio de variable \(t = 2^{2x}\):
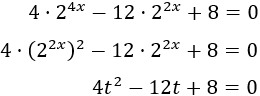
Dividimos entre 4 la ecuación de segundo grado y la resolvemos:
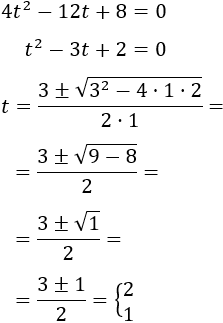
Como \(t = 2^{2x}\), tenemos
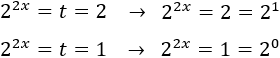
De la primera ecuación tenemos
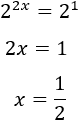
Y de la segunda,
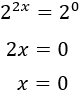
La ecuación exponencial tiene dos soluciones reales.
Ecuación exponencial con raíces
Como las raíces son potencias con fracciones en los exponentes, podemos encontrar ecuaciones exponenciales con signos radicales. Las resolveremos prácticamente del mismo modo.
Hay que recordar que
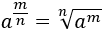
Por ejemplo, resolvemos la siguiente ecuación que tiene la incógnita en una raíz:
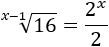
Escribimos la raíz y el número 16 como potencias:
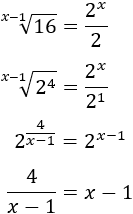
Para resolver la ecuación anterior, pasamos \(x-1\) multiplicando al otro lado:
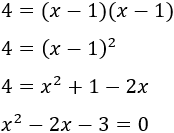
Resolvemos la ecuación de segundo grado:
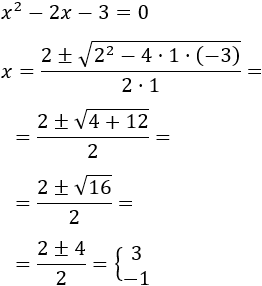
La ecuación exponencial tiene dos soluciones: \(x = 3\) y \(x = -1\).
Ecuación 12
Resolver escribiendo las raíces como potencias:
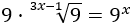
Solución:
Pasamos el 9 de la izquierda a la derecha y reescribimos la ecuación en forma de potencias:
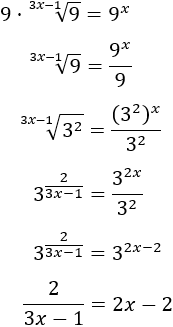
Resolvemos la ecuación:
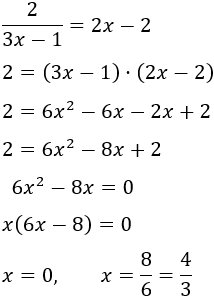
Por tanto, la ecuación exponencial tiene dos soluciones: \(x = 0\) y \(x = 4/3\).
Soluciones logarítmicas
Si no tenemos potencias con la misma base, la solución de la ecuación suele ser un logaritmo. Para trabajar estas ecuaciones, tenemos que utilizar las propiedades de los logaritmos.
La definición del logaritmo de base \(b\) es
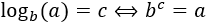
En otras palabras, el logaritmo en base \(b\) del número \(a\) es el número al que hay que elevar \(b\) para obtener \(a\). Por ejemplo, el logaritmo en base 2 de 8 es 3 porque 2 elevado a 3 es 8:
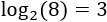
La solución de la ecuación \(3^x = 5\) es el número al que hay que elevar 3 para obtener 5, es decir, es precisamente el logaritmo en base 3 de 8 (aplicar logaritmos en ambos lados de la igualdad):
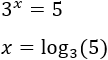
Otra forma de entender lo anterior es:
Como \(3^x\) debe ser igual a 5, entonces el logaritmo en base 3 de \(x\) debe ser igual al logaritmo en base 3 de 5:
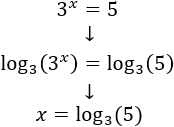
El último paso se debe a la definición del logaritmo: el logaritmo en base 3 de \(3^x\) es el número al que hay que elevar 3 para obtener \(3^x\).
Ecuación 13
Resolver mediante logaritmos en base 2:
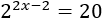
Solución:
Como la base de la exponencial es 2, aplicamos logaritmos en base 2 a ambos lados:
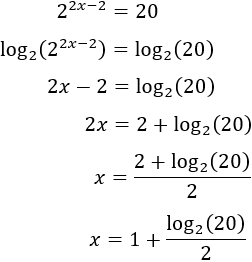
La solución puede simplificarse si aplicamos las propiedades del logaritmo:
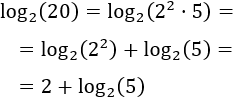
Por tanto,
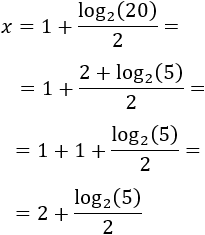
También, podemos escoger un logaritmo en base distinta a las bases de las exponenciales. Por ejemplo, aplicamos logaritmo en base 10 para resolver la siguiente ecuación:
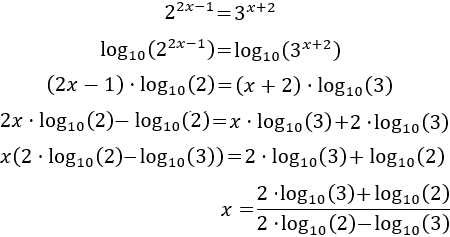
En adelante, si no escribimos la base de un logaritmo es porque ésta es 10.
Ecuación 14
Resolver la ecuación exponencial siguiente aplicando un cambio de variable (primero) y logaritmos en base 2 (después):
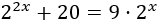
Solución:
Tendremos que aplicar el cambio de variable \(t=2^x\):
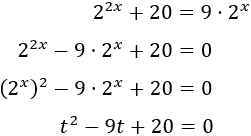
Las soluciones de la ecuación de segundo grado son
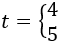
Como \(t = 2^x\), hemos obtenido que
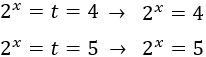
De la primera ecuación tenemos la solución \(x = 2\). De la segunda ecuación obtenemos una solución logarítmica:
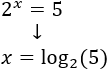
Ecuación 15
Resolver mediante logaritmos en base 5:
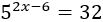
Solución:
Si escribimos 32 como una potencia tenemos
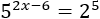
No podemos igualar los exponentes como hacíamos antes ya que las bases no son iguales, así que aplicamos logaritmos en base 5:
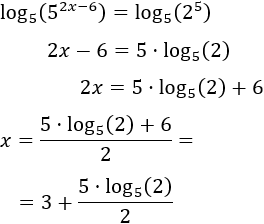
Ecuación 16
Resolver mediante logaritmos en base 10:
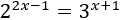
Solución:
Aplicamos logaritmos:
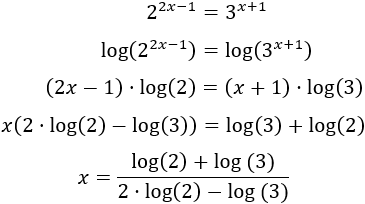
Ecuación 17
Resolver mediante logaritmos en base 10:
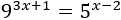
Solución:
Antes de aplicar logaritmos, escribimos el 9 como una potencia: