Introducción a las progresiones
En este texto damos el concepto de progresión, los tipos básicos y el término general. También, hablamos un poco de las progresiones aritméticas y geométricas (diferencia, razón y término general). Se incluyen ejemplos y problemas resueltos de los conceptos vistos.
Primeras definiciones
Una progresión o sucesión matemática es una secuencia ordenada de números que puede ser finita o infinita. A cada uno de los números se le denomina término y se le representa por \(a_n\), siendo \(n\) la posición del término en la secuencia.
Ejemplos:
-
La progresión de los números impares es una secuencia infinita: 1, 3, 5, 7, 9, 11, 13, 15,... El primer término es \(a_1 = 1\) y el quinto término es \(a_5 = 9\).
-
La progresión 1, 2, 3, 4 y 5 es finita (sólo consta de cinco términos). El segundo término es \(a_2=2\) y el cuarto es \(a_4 = 4\).
Una progresión puede ser
-
Creciente: si cada término es mayor o igual que el término que ocupa una posición anterior (\(a_{n+1}\geq a_n\)).
Ejemplo: 1, 2, 3, 4, 5,...
-
Decreciente: si cada término es menor que el término que ocupa una posición anterior (\(a_{n+1}\leq a_n\)).
Ejemplo: 7, 5, 3, 1, -1,...
-
Constante: si todos los términos son iguales (\(a_{n+1}= a_n\)).
Ejemplo: 1, 1, 1, 1, 1,...
-
Alternada: si el signo de cada término es distinto del signo del término anterior.
Ejemplo: 1, -2, 4, -8, 16, -32,...
Problema 1
Determinar si las siguientes progresiones son finitas o infinitas y si son crecientes, decrecientes, constantes o alternadas:
-
0, 2, 4, 6, 8, 10,...
-
3, 1, -1 y -3.
-
1, -5, 10, -15, 20, -25,...
Solución:
La primera progresión es infinita y creciente.
La segunda progresión es finita y decreciente, pero no es alternada.
La tercera progresión es infinita y alternada, pero no es creciente ni decreciente.
Problema 2
Deducir los siguientes dos términos que siguen en las siguientes sucesiones infinitas. ¿Son crecientes o decrecientes?
-
10, 20, 30, 40,...
-
1, 2, 4, 8, 16, 32,...
-
320, -160, 80, -40, 20,...
Solución:
La primera sucesión es la de los múltiplos de 10. El quinto término es \(a_5 = 50\) y el sexto es \(a_6 = 60\). Es una sucesión creciente.
La segunda sucesión es la de las potencias de 2. Cada término se obtiene multiplicando por 2 el término anterior. El séptimo término es \(a_7 = 64\) y el octavo es \(a_8 = 128\). Es una sucesión creciente.
Cada término de la tercera sucesión se obtiene dividiendo entre 2 el término anterior y cambiando su signo. El sexto término es \(a_6=-10\) y el séptimo es \(a_ 7 = 5\). La sucesión no es creciente ni decreciente, sino alternada.
Término general
El término general de una sucesión es la fórmula \(a_n\) que permite conocer cada término en función de su posición \(n\).
Ejemplos:
-
El término general de la progresión de los números impares (1, 3, 5, 7,...) es
$$a_n = 2\cdot n-1$$
Utilizamos el término general para calcular algunos sus términos sustituyendo la posición \(n\):
\(a_1 = 2\cdot 1 -1= 1\)
\(a_2 = 2\cdot 2 -1= 3 \)
\(a_3 = 2\cdot 3-1 = 5 \)
-
El término general de la sucesión 1, 4, 9, 16, 25, 36,... es
$$ a_n = n^2 $$
Problema 3
Calcular los cuatro primeros términos de las siguientes progresiones a partir de sus términos generales:
-
\(a_n = 3n -1\)
-
\(a_n = (-1)^n \cdot n\)
-
\(a_{n+1} = a_{n}+a_{n-1}\) siendo \(a_1 = 1\) y \(a_2 = 1\).
Solución:
Progresión a:
El primer término es \(a_1 = 3\cdot 1 -1= 2\).
El segundo término es \(a_2 = 3\cdot 2 -1 = 5\).
El tercer término es \(a_3 = 3\cdot 3 -1= 8\).
El cuarto término es \(a_4 = 3\cdot 4 -1 = 11\).
Es una sucesión creciente: 2, 5, 8, 11,...
Progresión b:
El primer término es \(a_1 =(-1)^1 \cdot 1 = -1\).
El segundo término es \(a_2 = (-1)^2 \cdot 2= 2\).
El tercer término es \(a_3 = (-1)^3 \cdot 3= -3\).
El cuarto término es \(a_4 = (-1)^4 \cdot 4= 4\).
Es una sucesión alternada: -1, 2, -3, 4,...
Progresión c:
-
El primer término es \(a_1 = 0\).
-
El segundo término es \(a_2 = 1\).
-
Calculamos el tercer término:
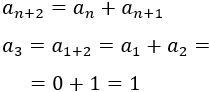
-
Calculamos el cuarto término:
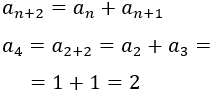
Es una sucesión creciente. Esta sucesión es muy famosa y se conoce como la sucesión de Fibonacci. Cada término (a partir del tercero) se obtiene sumando los dos términos anteriores: 0, 1, 1, 2, 3, 5, 7,...
Progresión aritmética
Una progresión es aritmética si cada término se obtiene sumando un número constante (diferencia) al término anterior.
Ejemplos:
-
100, 105, 110, 115, 120, ... es una sucesión aritmética cuya diferencia es \(d = 5\).
-
-5, -3, -1, 1, 3 y 5 es una sucesión aritmética (finita) cuya diferencia es \(d = 2\).
-
1, 4, 9, 16, 25, 36,... no es una sucesión aritmética porque, aunque el segundo término se obtiene sumando 3 al primero, no ocurre lo mismo con los siguientes.
El término general de una progresión aritmética es
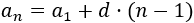
Si la diferencia \(d\) de la progresión es un número positivo, la progresión es creciente. Si \(d\) es negativo, la progresión es decreciente.
Problema 4
Calcular los tres términos siguientes de las sucesiones sabiendo que son aritméticas con diferencia \(d = 6\):
-
0, 6, 12,...
-
5, 11, 17,...
Solución:
Como la diferencia de ambas sucesiones es \(d = 6\), cada término se obtiene sumando 6 al término anterior.
Tenemos que calcular los términos cuarto, quinto y sexto.
Sucesión a: 0, 6, 12,...
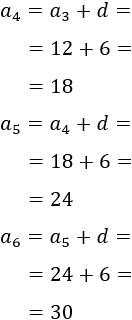
Sucesión b: 5, 11, 17,...
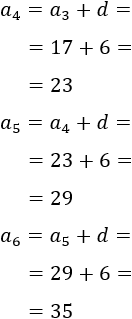
Problema 5
¿Cuál de las siguientes progresiones no es aritmética?
-
23, 24, 25, 26,...
-
3, 2, 1, 0, -1, -2, -3,...
-
0, 4, 16, 64,...
Solución:
En una progresión aritmética, la diferencia debe ser constante.
La primera progresión es aritmética con diferencia \(d = 1\).
La segunda progresión es aritmética con diferencia \(d = -1\).
La tercera progresión no es aritmética porque el segundo término es el primer término más 4, pero el tercer término es el segundo más 12 y el cuarto término es el tercero más 48. Como la diferencia no es constante, no es una progresión aritmética.
Problema 6
Calcular las diferencias de las siguientes progresiones aritméticas:
-
11, 14, 17, 20,...
-
1, 1.5, 2, 2.5, 3,...
-
10, 5, 0, -5, -10, ...
¿Cuál es el quinto y el sexto término de estas sucesiones?
Solución:
La diferencia se calcula restando términos consecutivos. Es aconsejable calcular la diferencia utilizando términos distintos para asegurarse de que realmente es una progresión aritmética (la diferencia debe ser la misma).
-
Progresión a: 11, 14, 17, 20,...
La resta del segundo y primer término es
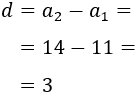
La del tercero y la del segundo es
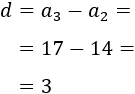
La diferencia de la progresión es \(d = 3\).
Como el cuarto término es \(a_4 = 20\), el quinto término y el sexto término son
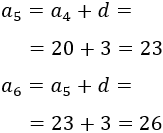
-
Progresión b: 1, 1.5, 2, 2.5, 3,...
La resta del segundo y primer término es
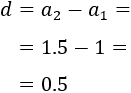
La del tercero y la del segundo es
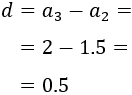
La diferencia de la progresión es \(d = 0.5\).
Como el quinto término es \(a_5 = 3\), el sexto término es
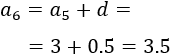
-
Progresión c: 10, 5, 0, -5, -10, ...
La resta del segundo y primer término es
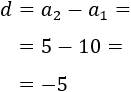
La del tercero y la del segundo es
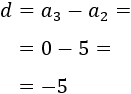
La diferencia de la progresión es negativa: \(d = -5\).
Como el quinto término es \(a_5 = -10\), el sexto término es
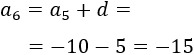
Problema 7
Calcular la fórmula general de las sucesiones del problema anterior.
Solución:
En una progresión aritmética, el término general se calcula a partir del primer término y de la diferencia:
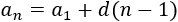
La diferencia de la sucesión 11, 14, 17, 20,… es \(d = 3\) y el primer término es \(a_1 = 11\). Su término general es
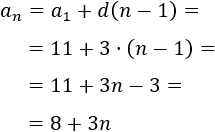
La diferencia de la sucesión 1, 1.5, 2, 2.5, 3,… es \(d = 0.5\) y el primer término es \(a_1 = 1\). Su término general es
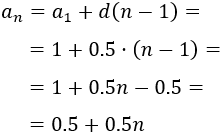
La diferencia de la sucesión 10, 5, 0, -5, -10, … es \(d = -5\) y el primer término es \(a_1 = 10\). Su término general es
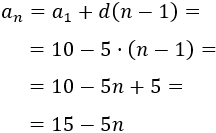
Progresión geométrica
Una progresión es geométrica si cada término se obtiene multiplicando un número constante (razón) por el término anterior.
Ejemplos:
-
1, 3, 9, 27, 81, … es una sucesión geométrica cuya razón es \(r = 3\).
-
6, 12, 24, 48, 96,… es una sucesión geométrica cuya razón es \(r = 2\).
-
5, 25, 50, 150,… no es una sucesión geométrica porque, aunque el segundo término se obtiene multiplicando por 5 al primero, no ocurre lo mismo con los siguientes.
El término general de una progresión geométrica es
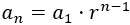
Si el primer término de una progresión geométrica es positivo, entonces:
-
Si la razón \(r\) de la progresión es un número positivo mayor que 1, la progresión es creciente.
-
Si \(r = 1\), la progresión es constante.
-
Si \(0< r< 1\), la progresión es decreciente.
-
Si \(r\) es negativo, la progresión es alternada (el signo va cambiando).
Ejemplos:
-
La sucesión 1, 2, 4, 8, 16,… es creciente porque la razón es \(r = 2> 1\).
-
La sucesión 2, 2, 2, 2,… es constante porque la razón es \(r = 1\).
-
La sucesión 80, 40, 20, 10, 5, 2.5,… es decreciente porque la razón es \(0< r = 0.5 < 1\).
-
La sucesión 1, -2, 4, -8, 16,… es alternada porque la razón es \(r = -2< 0\).
Problema 8
Calcular los dos términos siguientes de las sucesiones sabiendo que son geométricas con razón \(r = 3\):
-
5, 15,...
-
-2, -6, ...
La razón es positiva, pero las sucesiones son ¿crecientes o decrecientes?
Solución:
-
Sucesión a: 5, 15,...
El tercero y cuarto término son
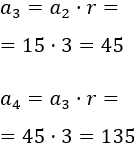
La sucesión es creciente.
-
Sucesión b: -2, -6, ...
El tercero y cuarto término son
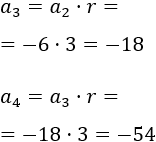
La sucesión es decreciente.
Problema 9
¿Cuál de las siguientes progresiones no es geométrica?
-
2, 6, 18, 54, ...
-
3, 9, -9, -18, ...
-
36, 18, 9, 4.5, ...
Solución:
La razón de una progresión geométrica debe ser simpre la misma.
La primera es geométrica porque la razón es \(r = 3\).
La tercera es geométrica porque la razón es \(r = 0.5\).
La segunda no es geométrica porque el segundo término se obtiene multiplicando por 3 al primer término (la razón sería 3), pero el cuarto término se obtiene multiplicando por 2 el tercero (la razón sería 2). No es geométrica porque la razón no se mantiene constante.
Problema 10
Calcular las razones de las siguientes progresiones geométricas:
-
4, 12, 36, ...
-
1, -5, 25, -125,...
-
8/3, 8/9, 8/27,...
Solución:
La razón se calcula dividiendo términos consecutivos.
-
Progresión a: 4, 12, 36, ...
El cociente entre el segundo y el primer término es
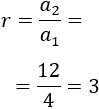
Y el cociente entre el tercer y el segundo término es
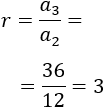
La razón es \(r = 3\).
-
Progresión b: 1, -5, 25, -125,...
El cociente entre el segundo y el primer término es
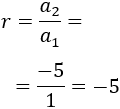
Y el cociente entre el tercer y el segundo término es
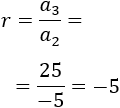
La razón es \(r = -5\).
-
Progresión c: 8/3, 8/9, 8/27,...
El cociente entre el segundo y el primer término es
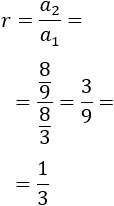
Y el cociente entre el tercer y el segundo término es
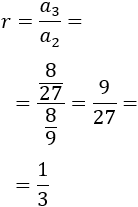
La razón es \(r = 1/3\).
Problema 11
Obtener las fórmulas generales de las progresiones geométricas del problema anterior.
Solución:
En una progresión geométrica, el término general se calcula a partir del primer término y de la razón:
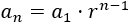
-
La razón de la sucesión 4, 12, 36,… es \(r=3\) y el primer término es \(a_1 = 4\). Su término general es
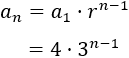
-
La razón de la sucesión 1, -5, 25, -125,… es \(r=-5\) y el primer término es \(a_1 = 1\). Su término general es
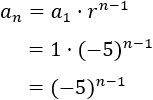
-
La razón de la sucesión 8/3, 8/9, 8/27,…es \(r=1/3\) y el primer término es \(a_1 = 8/3\). Su término general es
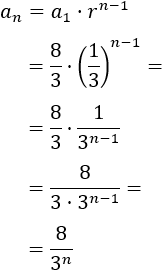
Para profundizar en las progresiones recomendamos 30 problemas resueltos de progresiones (matesfacil.com).