Calculadora del área y volumen de una esfera

Definimos esfera y proporcionamos 3 calculadoras para calcular el área y el volumen de una esfera a partir de su radio y viceversa. También, se incluyen problemas resueltos.

Índice:

Calculadoras
Superficie/sólido de revolución
Problemas resueltos

Una esfera de radio \(R\) y centro \(P\) es el conjunto de puntos del espacio que distan \(R\) del punto \(P\).

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

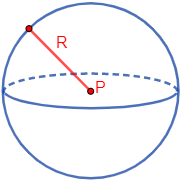
1. Calculadoras

Disponemos de tres calculadoras. Todas ellas utilizan las siguientes fórmulas del área y volumen:

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

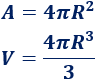
Los resultados se aproximan con 2 decimales.

Calculadora del área y volumen de la esfera a partir del radio:

Radio \(R =\)

Calculadora del radio y volumen a paritr del área:

Área \(A =\)

Calculadora del radio y área a paritr del volumen:

Volumen \(V =\)

2. Superficie/sólido de revolución

Una esfera es una superficie de revolución: se genera al hacer girar una circunferencia alrededor de un eje que pase por su centro:

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

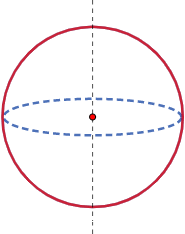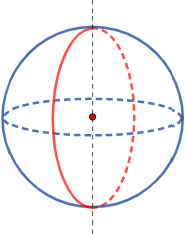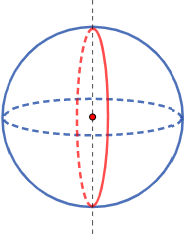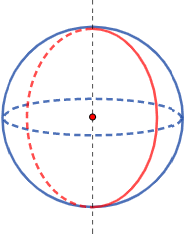
También, puede generarse al hacer girar una semicircunferencia.

Una esfera sólida es un sólido de revolución: se genera al hacer girar un círculo alrededor de un eje que pase por su centro:

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

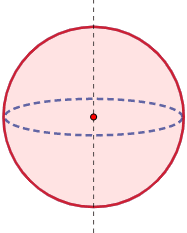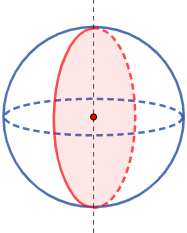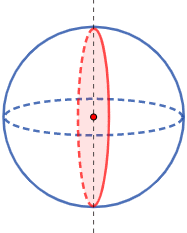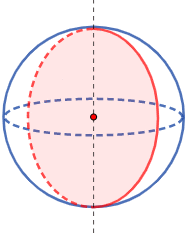
También, puede generarse al hacer girar un semicírculo.

3. Problemas resueltos

Problema 1

Calcular el área y el volumen de un esfera de radio \(R = 3 \text{ m}\).

Solución:

Sólo tenemos que sustituir en las fórmulas.

Calculamos el área:

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

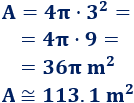
Calculamos el volumen:

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

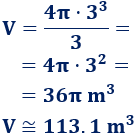
Los resultados coinciden, pero el área es en metros cuadrados y el volumen es en metros cúbicos.

Problema 2

Si el área de una esfera es \(A = 16\pi \text{ cm}^2\), ¿cuál es su volumen?

Solución:

Usamos la fórmula del área para calcular el radio:

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

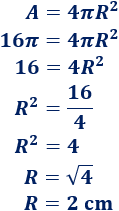
Ahora que conocemos el radio, podemos calcular el volumen:

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

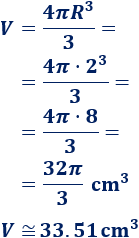
El volumen es, aproximadamente, \(33.51\text{ cm}^3\).

Problema 3

Si el volumen de una esfera es \(V = 4.5\pi \text{ m}^3\), ¿cuál es su área?

Solución:

Usamos la fórmula del volumen para calcular el radio:

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

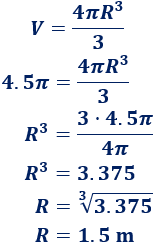
Calculamos el área:

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

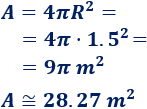
El área es \(9\pi\text{ m}^2\).

Problema 4

¿Cuántos litros de agua caben en un depósito esférico gigante de \(6\text{ m}\) de diámetro?

Solución:

El diámetro es el doble del radio, así que el radio de la esfera es \(3\text{ m}\).

Pasamos el radio a decímetros:

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

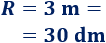
Calculamos el volumen de la esfera:

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

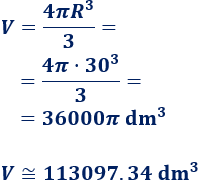
Como \(1\text{ L}\) de agua equivale a \(1\text{ dm}^3\), en el depósito caben, aproximadamente, \(113097.34\text{ L}\).

Problema 5

El radio de la esfera A es el doble que el de la esfera B. ¿El volumen de la esfera A es el doble que el de la esfera B?

Solución:

Si \(R\) es el radio de la esfera B, su volumen es

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

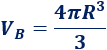
Como el radio de la esfera A es el doble que el de B, su volumen es

Calculadoras del área y volumen de una esfera (calcular área y volumen a partir del radio, calcular radio y volumen a partir del área y calcular radio y área a partir del volumen). La esfera como superficie y sólido de revolución. Fórmulas y problemas resueltos. Geometría del espacio. Matemáticas. Secundaria y bachillerato.

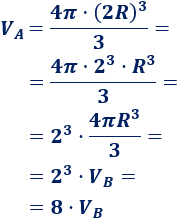
Por tanto, el volumen de la esfera A es \(8\) veces el de la esfera B, no el doble.

Más problemas similares:

Problemas y Ecuaciones ©

Volumen del cilindro

Área del círculo

Área del rombo

Calculadora de Pitágoras

Fracción equivalente e irreductible

Ecuaciones de primer grado

Problemas con ecuaciones

Problemas de sistemas

Ecuaciones de segundo grado

Ecuaciones exponenciales

Calculadora de porcentajes

Ecuaciones Resueltas

Universo matemático