Área y perímetro de un triángulo
Proporcionamos dos fórmulas para calcular el área de un triángulo, con ejemplos y problemas resueltos.
Índice:
- Introducción
- Perímetro
- Área
- Problemas resueltos
1. Introducción
Recordamos algunos conceptos clave:
- Un triángulo es un polígono de tres lados.
- Los vértices son los tres puntos en donde se unen dos lados (las esquinas).
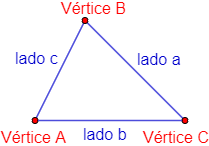
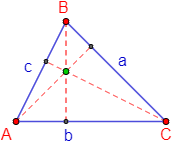
- La altura es el segmento de recta perpendicular que une un lado con el vértice opuesto a dicho lado.
-
Como hay tres lados, hay tres alturas. Las tres alturas se cortan en un único punto llamado ortocentro.
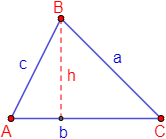
La base de un triángulo, \(b\), es cualquiera de sus tres lados (normalmente, se escoge el lado inferior paralelo al eje horizontal). Una vez escogida la base, llamaremos altura del triángulo, \(h\), a la altura perpendicular a la base.
2. Perímetro
El perímetro de un triángulo es la suma de las longitudes de sus tres lados.
Si los lados del triángulo miden \(a\), \(b\) y \(c\), entonces su perímetro es
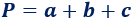
El semiperímetro de un triángulo es la mitad de su perímetro:
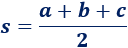
Ejemplo
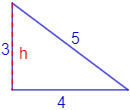
El perímetro del triángulo rectángulo de lados \(3\), \(4\) y \(5\) es \(12\):
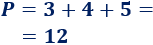
Y su semiperímetro es \(6\):
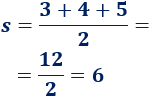
Observad que la altura del triángulo coincide con uno de sus lados.
El triángulo es rectángulo porque tiene un ángulo recto (ángulo de 90°).
3. Área
Tenemos varias formas de calcular el área de un triángulo: a partir de la base y la altura o a partir de sus lados y semiperímetro.
El área de un triángulo es la mitad del producto de su base por su altura:
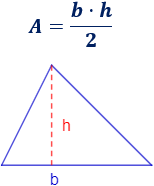
Ejemplo
El área del triángulo rectángulo de lados \(3\), \(4\) y \(5\) es \(6\):
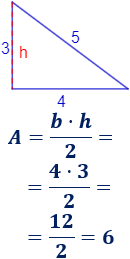
También, podemos calcular el área a partir de sus lados (\(a\), \(b\) y \(c\)) y de su semiperímetro (\(s\)) mediante la siguiente fórmula, llamada fórmula de Herón:
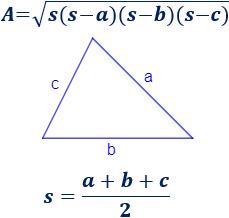
Ejemplo
Vimos en un ejemplo que el semiperímetro del triángulo rectángulo de lados \(3\), \(4\) y \(5\) es \(6\). Calculamos su área a partir de la fórmula de Herón:
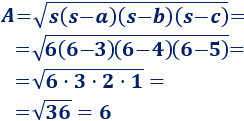
4. Problemas resueltos
Problema 1
Calcular el área del siguiente triángulo obtusángulo:
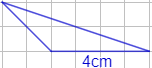
Solución:
Observando la cuadrícula, la altura del triángulo es \(2\text{ cm}\):
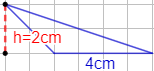
Como conocemos la altura y la base, podemos calcular el área:
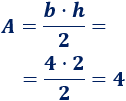
El área es \(4\text{ cm}^2\).
Problema 2
Calcular el área de un triángulo rectángulo sabiendo que uno de sus catetos mide \(2\text{ cm}\) y la hipotenusa mide \(\sqrt{13}\text{ cm}\).
Solución:
Es el siguiente triángulo:
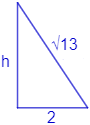
Para aplicar cualquiera de las dos fórmulas del área que tenemos, necesitamos saber cuánto mide el otro cateto, que es la altura del triángulo.
Podemos calcularlo aplicando el teorema de Pitágoras ya que se trata de un triángulo rectángulo.
Recordad que el teorema de Pitágoras establece que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de sus catetos. Por tanto,
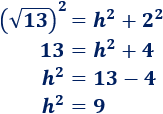
Hacemos la raíz cuadrada:
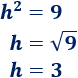
Por tanto, la altura de triángulo es \(3 \text{ cm}\).
Calculamos el área del triángulo:
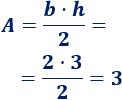
El área del triángulo es \(3\text{ cm}^2\).
Problema 3
Calcular el área del triángulo equilátero de lado \(4\text{ m}\).
Solución:
Los lados de un triángulo equilátero miden lo mismo, así que los tres lados miden \(4\text{ m}\):
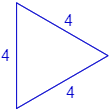
Podemos calcular la altura por Pitágoras, pero vamos a usar la fórmula de Herón, por variar.
El perímetro del triángulo es \(12\text{ m}\) y su semiperímetro es \(6\text{ m}\):
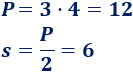
Calculamos el área:
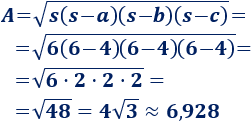
El área es \(4\sqrt{3}\text{ m}^2\), es decir, aproximadamente, \(6,928\text{ m}^2\).
Más problemas similares: áreas de triángulos.