Calculadora del área y volumen del cilindro
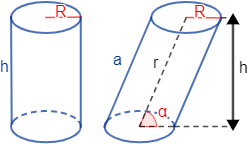
Calculadoras online para calcular el área y volumen de un cilindro recto y oblicuo. También, recordamos las fórmulas y proporcionamos algunos problemas resueltos sobre cilindros rectos.
Índice:
- Calculadora online del área y volumen
- Partes de un cilindro
- Área
- Volumen
- Sólido de revolución
- Problemas resueltos
1. Calculadora online del área y volumen
Nota: las calculadoras aproximan el resultado con 2 decimales.
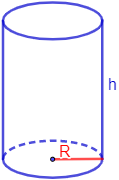
Introduce el radio (\(R\)) y la altura (\(h\)) del cilindro:
\(R =\)
\(h =\)
Hemos usado las fórmulas
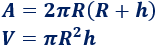
Cilindro oblicuo:
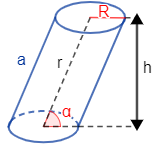
Introduce el radio (\(R\)), el lado (\(a\)) y la altura (\(h\)) del cilindro:
\(R =\)
\(h =\)
\(a =\)
Hemos usado las fórmulas
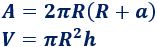
Observad que \(h = a·sin(\alpha )\).
Observación: la fórmula del volumen es la misma para el cilindro recto y el oblicuo. Sin embargo, no ocurre lo mismo con el área.
2. Partes de un cilindro
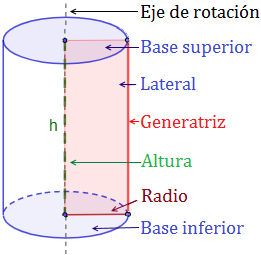
3. Área
Vamos a ver intuitivamente que el área de un cilindro de altura \(h\) y radio \(R\) es

El área del cilindro es la suma del área de las bases (superior e inferior) y del área lateral.
Desarmamos el cilindro:
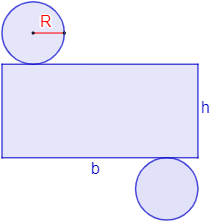
Las bases son dos círculos iguales de radio \(R\), así que su área total es

El lateral es un rectángulo de altura \(h\). La base del rectángulo debe medir lo mismo que el perímetro de las bases (círculos), es decir, \(b = 2\cdot \pi \cdot R\).
El área del rectángulo es

El área del cilindro de altura \(h\) y radio \(r\) es la suma del área lateral y de las bases:
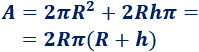
4. Volumen
Podemos imaginar un cilindro como un montón de monedas muy finas:

El volumen del montón es el área de una moneda multiplicada por la altura del montón.
Del mismo modo, el área de un cilindro es el producto del área de su base por su altura.
Si el radio del cilindro es \(R\) y su altura es \(h\), entonces su volumen es

5. Sólido de revolución
El cilindro recto es un sólido de revolución porque puede construirse al hacer girar un rectángulo alrededor de un eje:
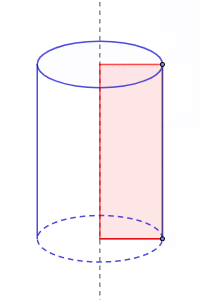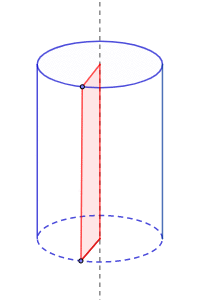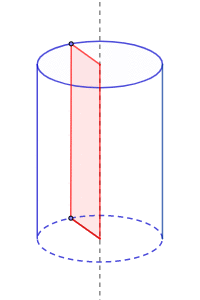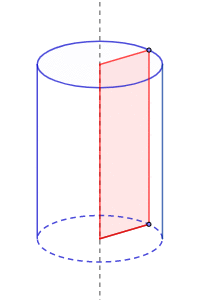
La altura del rectángulo es la altura del cilindro que se forma y la base es el radio.
Nota: el cilindro oblicuo (con bases circulares) no es un sólido de revolución.
6. Problemas resueltos
Problema 1
Calcular el área y el volumen de un cilindro de radio \(R = 3\text{ cm}\) y altura \(h = 1\text{ m}\).
Solución:
El radio es \(R = 3\text{ cm}\).
Como la altura está escrita en metros y el radio en centímetros, tenemos que cambiar una de las unidades.
Pasamos la altura a centímetros:
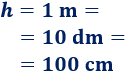
Calculamos el área:
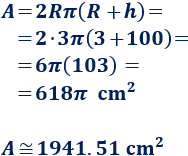
El área es, aproximadamente, \(1941.51 \text{ cm}^2\).
Calculamos el volumen:
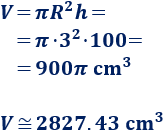
El volumen es, aproximadamente, \(2827.43 \text{ cm}^3\).
Problema 2
En un bote cilíndrico de \(5\text{ cm}\) de altura caben \(2\text{ L}\) de agua. ¿Cuánto mide el radio de la base del bote?
Solución:
Recordad que \(1\) litro equivale a \(1\) decímetro cúbico:

Por tanto, el volumen del bote es \( V = 2 \text{ dm}^3\).
La altura del bote es
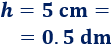
La fórmula del volumen de un cilindro es

Como conocemos \(V\) y \(h\), podemos calcular \(R\):
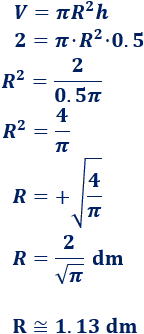
El radio mide, aproximadamente, \(1.13 \text{ dm}\). Es decir, unos \(11.3 \text{ cm}\).
Problema 3
Manuel quiere forrar con tela metálica un poste que tiene forma cilíndrica. El poste mide \(2.3\text{ m}\) de alto y \(25 \text{ cm}\) de diámetro. Si el precio de la tela es de \(10\) euros por metro cuadrado, ¿cuánto dinero necesita?
Solución:
Escribimos la altura del poste en centímetros:
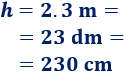
El diámetro es el doble del radio, así que el radio del poste es
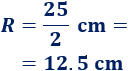
Calculamos el área del poste:
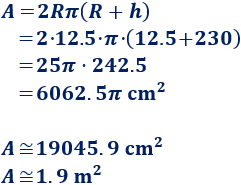
Manuel necesita, aproximadamente, \(19045.9\text{ cm}^2\) de tela. Es decir, aproximadamente \(1.9 \text{ m}^2\) de tela.
Necesita \(19\) euros para la tela.
Más problemas similares:
- Área del círculo
- Área del rombo
- Áreas de triángulos
- Cuadrados
- Pentágono regular
- Hexágono regular
- Corona circular
- Sector circular