Área y perímetro del círculo
Calculadora y problemas
Recordamos los conceptos de círculo y circunferencia, proporcionamos las fórmulas y una calculadora del área y del perímetro y resolvemos algunos problemas.
Índice:
- Perímetro y área
- Calculadora
- Circunferencia y círculo
- Problemas resueltos
1. Perímetro y área
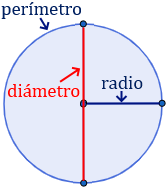
El perímetro de un círculo de radio \(r\) es la longitud de su lado (borde):

Como el diámetro de un círculo es dos veces su radio, \(d = 2·r\), podemos escribir el perímetro como

El área de un círculo es su superficie:

Ejemplo
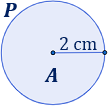
Calculamos el área y el perímetro de un círculo de radio \(r = 2\text{ cm}\):
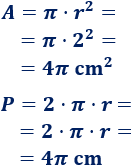
El área del círculo es \(4\pi \text{ cm}^2\) y el perímetro es \(4\pi \text{ cm}\). Observad que ambas magnitudes son iguales, pero cambian las unidades de medida. Esto sólo ocurre cuando el radio es \(r = 2\).
2. Calculadora del área y perímetro
Calculadora del área, \(A\), y perímetro, \(P\), de un círculo a partir de su radio, \(r\) (no se admiten fracciones ni raíces).
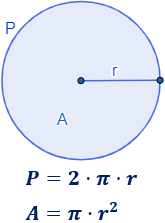
¿Cuál es el radio \(r\) del círculo?
\(r =\)
3. Circunferencia y círculo
¡El borde de un círculo es una circunferencia!
La circunferencia de radio \(r>0\) y centro \(c=(c_1,c_2)\) es el lugar geométrico del plano formado por los puntos cuya distancia al punto \(c\) es igual a \(r\).
Estos puntos \((x,y)\) son los que cumplen la ecuación

Representación:
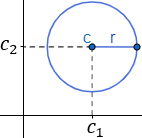
Ejemplo
La circunferencia centrada en el origen \( c=(0,0)\) y de radio \(r=1\) es
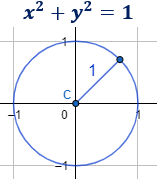
Observad que
- La distancia de los puntos de la circunferencia a su centro es exactamente 1.
- Como el centro de la circunferencia es (0, 0), la circunferencia pasa por los puntos (-1, 0), (1, 0), (0, 1) y (0, -1).
-
Las coordenadas de todos los puntos \((x,y)\) de la circunferencia cumplen la ecuación de la circunferencia \(x^2 + y^2 = 1\). Por ejemplo, los cuatro puntos anteriores cumplen la ecuación:
- Punto (-1, 0): $$ (-1)^2 + 0^2 = 1 $$
- Punto (1, 0): $$ 1^2 + 0^2 = 1 $$
- Punto (0, 1): $$ 0^2 + 1^2 = 1 $$
- Punto (0, -1): $$ 0^2 + (-1)^2 = 1 $$
- Los puntos que no cumplen la ecuación no están en la circunferencia. Por ejemplo, el punto (1, 1) está fuera de la circunferencia y no la cumple: $$ 1^2 + 1^2 = 2 \neq 1 $$
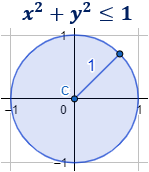
El círculo de radio \(r>0\) y centro \(c=(c_1,c_2)\) es el lugar geométrico del plano formado por los puntos cuya distancia al punto \(c\) es menor o igual que \(r\).
Estos puntos \((x,y)\) son los que cumplen la ecuación

Ejemplo
La circunferencia centrada en el origen \( c=(0,0)\) y de radio \(r=1\) es
4. Problemas resueltos
Problema 1
¿Cuál es el radio, el perímetro y el área del siguiente círculo?
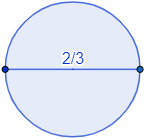
Solución:
En la figura se ha representado el diámetro del círculo y mide \(d=2/3\).
Como el diámetro es el doble del radio, el radio del círculo es
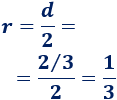
Calculamos el perímetro:
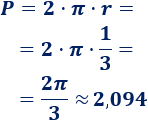
Calculamos el área:
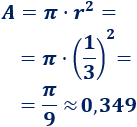
Problema 2
- Hallar el radio y el centro de la circunferencia dada por la ecuación
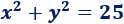
- Hallar la ecuación de la siguiente circunferencia:
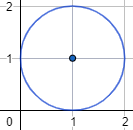
Solución:
- Observando la fórmula, sabemos que el centro es \((0,0)\) y el radio es

- Observando la figura, el centro es \((1,1)\) y el radio es \(1\), así que su ecuación es
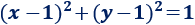
Problema 3
Hallar el radio y el centro del círculo dado por la ecuación
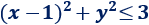
Solución:
El centro es \((1,0)\) y el radio es \(r = \sqrt{3}\).
Problema 4
Hallar el perímetro de la circunferencia dada por la siguiente ecuación y el área que ésta encierra:
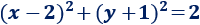
Solución:
Para calcular el área y el perímetro sólo necesitamos el radio, que es \(r = \sqrt{2}\).
Calculamos el perímetro:
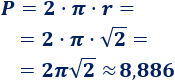
Calculamos el área:
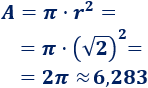
Problema 5
Hallar el radio del círculo cuya área es \(9\pi\).
Solución:
La fórmula del área es

Como sabemos que el área es \(9\pi\), podemos calcular el radio:
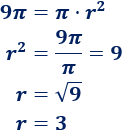
El área del círculo es \(r=3\).
Más problemas similares: áreas de figuras circulares.