Calculadora y demostración del área y perímetro de rectángulo
Proporcionamos tres calculadoras relacionadas con el área y el perímetro de un rectángulo, definimos rectángulo y demostramos las fórmulas del área y perímetro del mismo. También, resolvemos \(3\) problemas de aplicación de las fórmulas vistas.
Índice:
- Calculadoras
- Definición de rectángulo
- Perímetro
- Área
- Problemas resueltos
1. Calculadoras
Disponemos de \(3\) calculadoras:
- Calculadora del área y perímetro a partir de los lados.
- Calculadora del área y un lado a partir del perímetro y del otro lado.
- Calculadora del perímetro y un lado a partir del área y del otro lado.
Las calculadoras aproximan el resultado con \(2\) decimales.
Calculadora a partir de los lados (base y altura):
Base: \(b =\)
Altura: \(a =\)
Calculadora a partir del perímetro y un lado:
Perímetro: \(P =\)
Lado: \(L =\)
Calculadora a partir del área y un lado:
Área: \(A =\)
Lado: \(L =\)
2. Definición de rectángulo
Un rectángulo es un polígono de \(4\) lados (cuadrilátero), de modo que los lados opuestos son paralelos e iguales y los lados contiguos forman ángulos rectos:
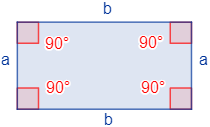
- Los lados \(a\) son opuestos, paralelos y con la misma longitud. Lo mismo ocurre con los lados \(b\).
- Los ángulos que forman los lados \(a\) y \(b\) entre sí son rectos (\(90^\circ\)).
- Normalmente, a los lados \(b\) se les llama base y a los lados \(a\), altura.
Un caso especial de rectángulo es el cuadrado:
Un cuadrado es un rectángulo cuyos lados tienen la misma longitud (se trata de un cuadrilátero regular).
La diagonal de un polígono es el segmento que une dos vértices no consecutivos. Un rectángulo tiene dos diagonales de igual longitud:
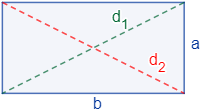
Como la diagonal divide en rectángulo en dos triángulos rectángulos, por aplicación del teorema de Pitágoras, su longitud es
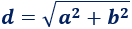
3. Perímetro
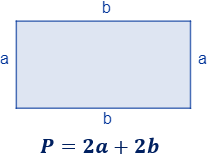
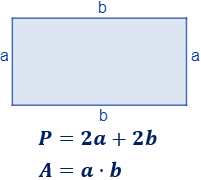
El perímetro es la suma de las longitudes de todos los lados, así que el perímetro de un rectángulo de altura \(a\) y base \(b\) es
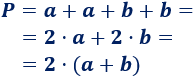
Por ejemplo, el perímetro de un rectángulo de base \(5\text{ cm}\) y altura \(2\text{ cm}\) es \(14\text{ cm}\):
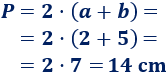
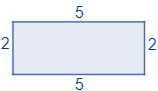
4. Área
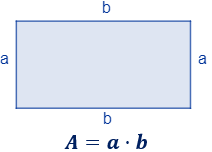
El área de un rectángulo es el producto de su base por su altura:
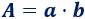
Por ejemplo, el área de un rectángulo de base \(5\text{ cm}\) y altura \(2\text{ cm}\) es \(10\text{ cm}^2\):
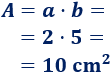
Demostración:
Vamos a demostrar esta fórmula con la ayuda de la fórmula del área de un cuadrado.
Recordad que el área de un cuadrado de lado \(L\) es
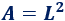
Para calcular el área de un rectángulo de base \(b\) y altura \(a\), representamos un cuadrado de lado \(a\), un cuadrado de lado \(b\) y dos rectángulos de base \(b\) y altura \(a\):
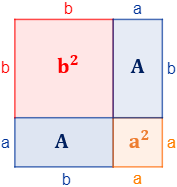
- En rojo tenemos el cuadrado de lado \(b\). Su área es \(b^2\).
- En naranja, el cuadrado de lado \(a\). Su área es \(a^2\).
- Y en azul, los dos rectángulos de lados \(a\) y \(b\). Tienen la misma área (\(A\)) porque son iguales.
Observad que los cuatro cuadriláteros conforman un único cuadrado y su área es la suma de las cuatro áreas:
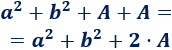
Ahora bien, observad que este cuadrado tiene lado \(a+b\), así que su área es
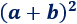
Desarrollamos el cuadrado de la suma:
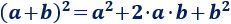
Igualamos ambos áreas:
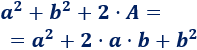
De esta igualdad obtenemos el área del rectángulo de lados \(a\) y \(b\):
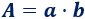
5. Problemas resueltos
A continuación, resolvemos algunos problemas de aplicación de las fórmulas del área y perímetro de un rectángulo.
Problema 1
¿Cuál es la altura de un rectángulo de perímetro \(14\text{ cm}\) si su base mide \(3\text{ cm}\)?
Solución:
La base del rectángulo es \(b=3\) y la altura es \(a\).
La fórmula del perímetro es

Sustituimos \(P = 14\) y \(b=3\) y resolvemos la ecuación:
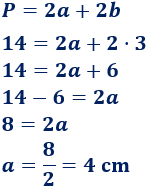
Por tanto, la altura del rectángulo es \(4\text{ cm}\).
Problema 2
¿Cuál es el área de un rectángulo de perímetro \(18\text{ cm}\) si su altura mide \(2\text{ cm}\)?
Solución:
La altura del rectángulo es \(a = 2\).
La fórmula del perímetro es

Sustituimos \(P = 18\) y \(a=2\) y resolvemos la ecuación:
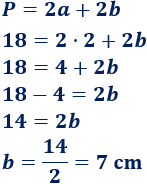
La base es \(b=7\).
Calculamos el área del rectángulo:
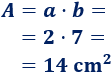
El área del rectángulo es \( 14\text{ cm}^2\).
Problema 3
¿Cuánto miden los lados de un rectángulo si su perímetro es \(16\text{ m}\) y su área es \(15\text{ m}^2\)?
Solución:
La fórmula del perímetro es

Y la del área es
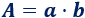
Como \(P=16\) y \(A = 15\), tenemos dos ecuaciones con dos incógnitas:
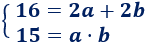
No se trata de un sistema de ecuaciones lineales, pero es fácil de resolver.
Dividimos la primera ecuación entre \(2\):
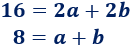
Aislamos \(b\) en la segunda ecuación:
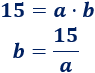
Sustituimos en la primera ecuación:
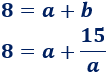
Operamos:
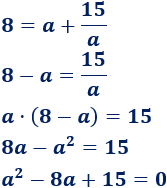
Resolvemos la ecuación de segundo grado completa:
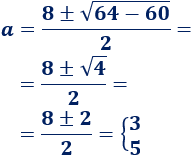
Tenemos dos soluciones: \(a = 3\) y \(a = 5\).
Si \(a = 3\), entonces
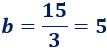
Si \(a = 5\), entonces
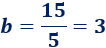
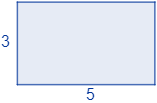
Ambas soluciones proporcionan el mismo rectángulo (el de lados \(3\) y \(5\) metros):
Otras calculadoras:
- Área y perímetro del círculo
- Área y perímetro del rombo
- Área y perímetro del pentágono
- Área y perímetro del hexágono
- Área y perímetro del heptágono
- Área y perímetro del octágono
- Área y perímetro del eneágono
- Área y perímetro del decágono
- Área y perímetro del endecágono
- Área y perímetro del dodecágono
- Área y perímetro del tridecágono
- Área y volumen del cono
- Área y volumen de la esfera
- Área y volumen del cilindro
- Área y volumen del tronco de cono
- Área y volumen del prisma triangular
- Área y volumen del prisma pentagonal
- Área y volumen del prisma hexagonal
- Área y volumen del prisma heptagonal