Calculadora del área y volumen del cono
En esta página proporcionamos distintas calculadoras online para calcular el área y volumen de un cono recto con base circular a partir de distintos datos (altura, altura inclinada, radio y apertura). También, demostramos las fórmulas del área y del volumen y resolvemos algunos problemas de aplicación.
Índice:
- Calculadoras del área y volumen
- Definición y elementos del cono
- Fórmula del área
- Fórmula del volumen
- Problemas resueltos
1. Calculadoras del área y volumen
Disponemos de 4 calculadoras calculadoras para calcular el área y el volumen según los datos de los que disponemos:
- Radio y altura.
- Radio y altura inclinada.
- Altura y altura inclinada.
- Apertura (ángulo) y altura inclinada.
Nota: la altura inclinada también se llama generatriz.
Las calculadoras aproximan el resultado con 2 decimales.
Calculadora a partir del radio y la altura:
\(R =\)
\(h =\)
Calculadora a partir del radio y la altura inclinada:
\(R =\)
\(a =\)
Calculadora a partir de la altura y la altura inclinada:
\(h =\)
\(a =\)
Calculadora a partir del ángulo (apertura) en grados y altura inclinada:
\(\alpha =\) º
\(a =\)
2. Definición y elementos del cono
Definición de cono
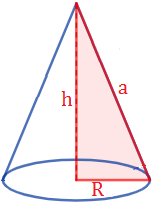
Un cono es el cuerpo geométrico que se genera al hacer girar un triángulo rectángulo (generatriz) sobre uno de sus catetos:
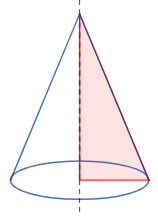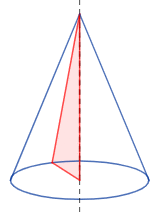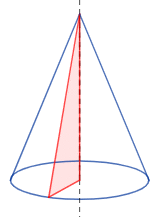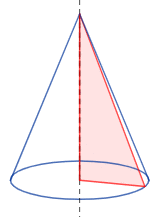
Este cono es, en concreto, un cono recto con base circular. Existen otros tipos de conos, como el cono con base elíptica o el cono oblicuo (la altura no forma un ángulo recto con la base).
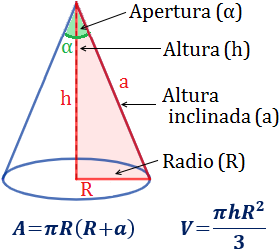
Elementos del cono
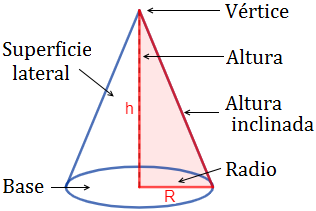
Observad que el radio del cono coincide con uno de los catetos del triángulo que genera el cono; la altura, con el otro cateto; y la altura inclinada, con la hipotenusa.
Además, se llama
- directriz al perímetro de la base del cono (curva plana circular).
- apertura al ángulo máximo entre dos segmentos generatrices de la superficie lateral (segmentos que unen puntos de la directriz con el vértice). Si \(\alpha\) es el ángulo que forman la altura y la altura inclinada, entonces la apertura es \(2\alpha\):
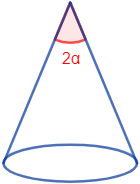
3. Fórmula del área
Vamos a demostrar que el área del cono de radio \(R\) y altura inclinada \(a\) es
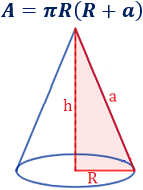
También, podemos utilizar la siguiente fórmula con la altura del cono en lugar de la altura inclinada:
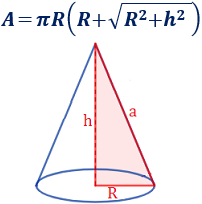
Esta segunda fórmula se obtiene escribiendo la altura inclinada en función del radio y la altura por aplicación del teorema de Pitágoras (ver problema 3).
Demostración (primera fórmula)
El área del cono es la suma del área de su base y del área de su superficie lateral.
Desarrollo plano del cono:
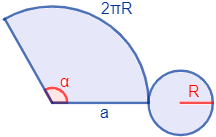
Tenemos que calcular el área coloreada de azul.
El área de la base del cono es \(\pi R^2\) por ser un círculo de radio \(R\).
Observad que
- El segmento curvo (arco) del sector circular mide \(2\pi R\) puesto que debe coincidir con la directriz (el perímetro de la base).
- El segmento \(a\) es la altura inclinada del cono. Es el radio del sector circular.
Falta calcular el área del sector circular.
Como el área de un círculo de radio \(a\) es \(\pi a^2\), el área del sector circular de ángulo \(\alpha\) es
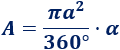
Es decir, hemos dividido el área entre los \(360^\circ\) que tiene un círculo y multiplicado por el ángulo del sector circular.
Ahora necesitamos calcular el ángulo \(\alpha\).
Como el perímetro del círculo al que pertenece el sector circular es \(2\pi a\), debe cumplirse
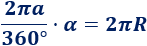
Entonces,
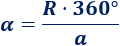
Sustituyendo en el área,
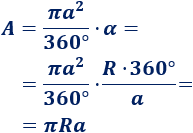
Por tanto, el área total del cono es
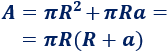
4. Fórmula del volumen
Vamos a demostrar que el volumen del cono de altura \(h\) y radio \(R\) es
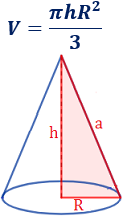
Si cortamos el cono en planos paralelos a la base obtenemos círculos de distinto radio \(r\).
Por tanto, podemos calcular el volumen del cono sumando las áreas de todos estos círculos:
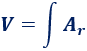
El radio \(r\) del círculo obtenido al cortar el cono depende de la altura \(y\) a la que se realiza el corte:
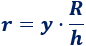
Por tanto, el área de cada círculo es
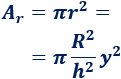
Calculamos el volumen:
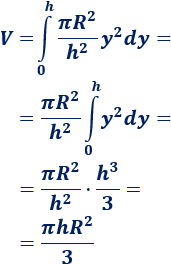
5. Problemas resueltos
Problema 1
Calcular el área de un cono de altura inclinada \(15\text{ cm}\) y diámetro \( 6\text{ cm}\).
Solución:
Como el diámetro es el doble del radio, el radio del cono es \(R =3\).
Calculamos el área del cono:
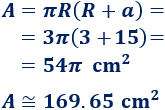
Problema 2
Calcular el volumen de un cono de altura \( 5\text{ dm}\) y radio \( 0.3\text{ m}\).
Solución:
Escribimos el radio en decímetros para tener las mismas unidades:
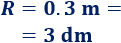
Sustituimos en la fórmula del volumen:
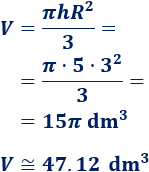
Problema 3
Calcular el área de un cono de altura \( 3\text{ cm}\) y radio \(4 \text{ cm}\).
Solución:
La fórmula del área es

Recordad que \(a\) es la altura inclinada del cono, no la altura del cono. Necesitamos calcular \(a\) para poder usar la fórmula.
Aplicando el teorema de Pitágoras,
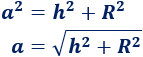
Calculamos la altura inclinada:
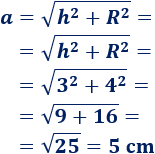
Calculamos el área del cono:
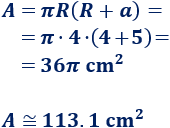
Problema 4
Calcular el área de un cono de altura \( 1\text{ dm}\) y altura inclinada \( 2\text{ dm}\).
Solución:
La fórmula del área es

Necesitamos el radio para poder usar la fórmula.
En el problema anterior ya vimos que, por Pitágoras,
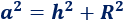
Como conocemos \(a\) y \(h\), podemos calcular \(R\):
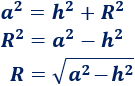
Sustituimos los datos:
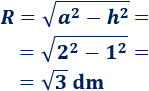
Calculamos el área:
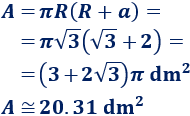
Problema 5
José tiene dos conos de igual altura: uno rojo de \( \text{3 cm}\) de radio y otro azul de \(6 \text{ cm}\) de radio. ¿El cono azul tiene el doble de volumen que el rojo?
Solución:
La altura de ambos conos es \(h\).
El volumen del cono rojo es
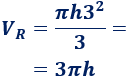
El volumen del cono azul es
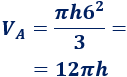
El cono azul tiene el cuádruple de altura que el cono rojo.
Problema 6
Ana tiene dos conos de igual radio: uno rojo de \( \text{5 cm}\) de altura y uno azul de \(10 \text{ cm}\) de altura. ¿El cono azul tiene el doble de volumen que el rojo?
Solución:
El radio de ambos conos es \(r\).
El volumen del cono rojo es
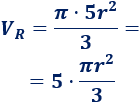
El volumen del cono azul es
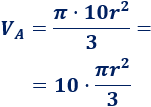
El cono azul tiene el doble de volumen que el rojo.
Más problemas similares: Problemas