Calculadora del área y volumen de la pirámide cuadrada
Proporcionamos una calculadora del área y volumen de la pirámide cuadrada y demostramos las fórmulas del área y volumen de ésta.
Índice:
- Calculadoras del área y volumen
- Definición y arista de la pirámide cuadrada
- Fórmula del área
- Fórmula del volumen
1. Calculadoras del área y volumen
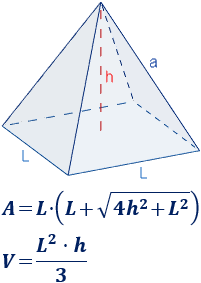
La calculadora aproxima el resultado con \(n\) decimales.
Calculadora:
Lado de la base: \(L =\)
Altura de la pirámide: \(h =\)
Decimales: \(n =\)
2. Definición y arista de la pirámide cuadrada
Una pirámide cuadrada (o cuadrangular) es una pirámide con base cuadrada. Este poliedro tiene \(5\) caras (\(1\) base y \(4\) caras laterales), \(8\) aristas y \(5\) vértices:
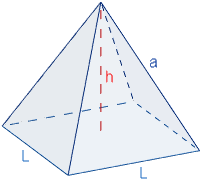
- \(h\) es la altura de la pirámide
- \(L\) es el lado del cuadrado de la base
- \(a\) son las aristas laterales
La pirámide es recta cuando la proyección del vértice superior sobre la base coincide con su centro. Si no, la pirámide es oblicua:
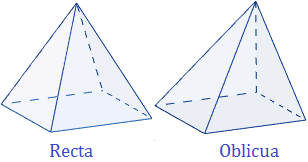
Nosotros supondremos siempre que la pirámide es recta.
Las caras laterales de la pirámide son \(4\) triángulos isósceles iguales. La base de estos triángulos es \(L\) y el lado depende de la altura de la pirámide (\(h\)).
A continuación, calculamos la arista lateral de la pirámide.
Arista de la pirámide cuadrada
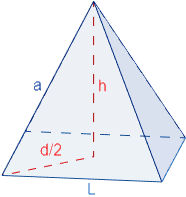
Si \(d\) es la diagonal del cuadrado, por Pitágoras,
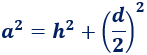
Recordad que (aplicando Pitágoras) la diagonal del cuadrado de lado \(L\) es
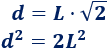
Por tanto,
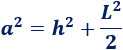
Luego la arista lateral de la pirámide es
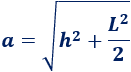
3. Fórmula del área
El área de una pirámide cuadrada de lado \(L\) y altura \(h\) es
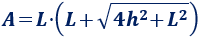
Demostración:
El área de la pirámide es la suma del área de las caras laterales y del área de la base:
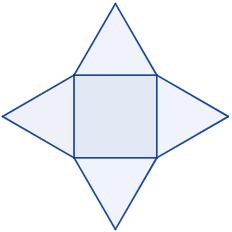
Como la base es un cuadrado de lado \(L\), su área es
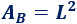
Las caras laterales son \(4\) triángulos de base \(L\).
¡La altura de los triángulos no es la altura de la pirámide! Esto se debe a que las caras laterales están inclinadas. A la altura de estos triángulos suele llamarse altura inclinada de la pirámide.
Podemos calcular su altura (\(r\)) a partir de la arista, la cual ya hemos calculado anteriormente.
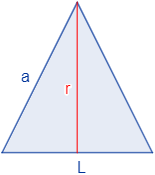
Por Pitágoras,
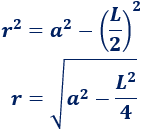
Sustituyendo la arista,
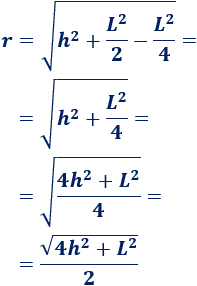
El área que suman los cuatro triángulos de base \(L\) y altura \(r\) es
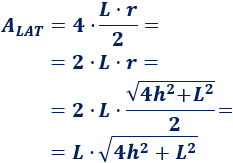
Luego el área de la pirámide cuadrada de lado \(L\) y altura \(h\) es
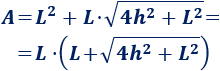
4. Fórmula del volumen
El volumen de la pirámide cuadrada de lado \(L\) y altura \(h\) es
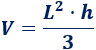
Nota: esta fórmula sirve para la pirámide oblicua.
Demostración:
Las secciones de la pirámide paralelas a la base son cuadrados de lado menor cuanto más alto sea el corte:
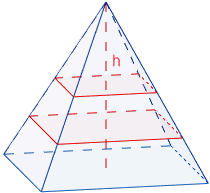
Observad que estos cuadrados son perpendiculares a la altura de la pirámide.
La suma de las áreas de todas las secciones de la pirámide es su volumen.
Supongamos que \(y(x)\) es el lado del cuadrado de la sección de la pirámide a la altura \(x\).
Lógicamente, cuando \(x=0\), \(y(x) = L\); y cuando \(x =h\), \(y(x) = 0\). Por tanto, el lado es
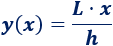
El área de dicha sección (cuadrado) es
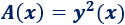
Así, pues, el volumen de la pirámide es
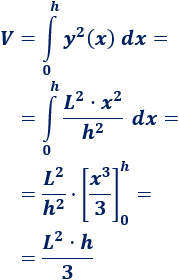
Otras calculadoras:
- Área y perímetro del círculo
- Área y perímetro del rectángulo
- Área y perímetro del rombo
- Área y perímetro del pentágono
- Área y perímetro del hexágono
- Área y perímetro del heptágono
- Área y perímetro del octágono
- Área y perímetro del eneágono
- Área y perímetro del decágono
- Área y perímetro del endecágono
- Área y perímetro del dodecágono
- Área y volumen del cono
- Área y volumen de la esfera
- Área y volumen del cilindro
- Área y volumen del tronco de cono
- Área y volumen del prisma triangular
- Área y volumen del prisma pentagonal
- Área y volumen del prisma hexagonal
- Área y volumen del prisma heptagonal
- Área y volumen del casquete esférico