¿Qué es una ecuación lineal?
En esta página explicamos qué es una ecuación lineal y proporcionamos algunos ejemplos de ecuaciones lineales y de ecuaciones no lineales.
Índice:
- Ecuación lineal
- Soluciones de una ecuación lineal
- Ecuación no lineal
- Problemas resueltos
1. Ecuación lineal
Definición informal de ecuación lineal
Las ecuaciones más simples son las lineales. Pueden tener una o varias incógnitas, pero las incógnitas sólo pueden sumarse o restarse entre sí.
Las incógnitas no pueden multiplicarse, ni tener exponentes, ni estar dentro de raíces, logaritmos o valores absolutos, etc.
Ejemplos
- Ecuación lineal con dos incógnitas (\(x\) e \(y\)):
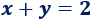
- Ecuación lineal con tres incógnitas (\(x\), \(y\) y \(z\)):

- Ecuación no lineal con dos incógnitas (\(x\) e \(y\)):
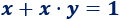
- Ecuación no lineal con dos incógnitas (\(x\) e \(y\)):
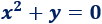
- Ecuación no lineal con dos incógnitas (\(x\) e \(y\)):
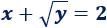
Definición matemática de ecuación lineal
Una ecuación lineal con N incógnitas (\(x_1\), \(x_2\),… \(x_N\)) tiene la forma
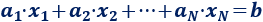
siendo \(a_1\), \(a_2\),… \(a_N\) y \(b\) números.
2. Soluciones de una ecuación lineal
Una ecuación lineal con \(1\) incógnita (\(x\)), tiene la siguiente forma (siendo \(a\neq 0\)):
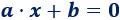
Esta ecuación tiene una única solución y es
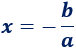
Estas ecuaciones son las ecuaciones de primer grado.
Una ecuación lineal con más de una incógnita tiene infinitas soluciones.
Ejemplo
Consideremos la ecuación
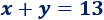
Una solución de esta ecuación es \(x = 1\) e \(y = 12\) (porque 1 + 12 = 13), pero hay otras soluciones (infinitas, de hecho), por ejemplo:
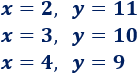
Ahora bien, si consideramos un conjunto de ecuaciones lineales que comparten incógnitas, puede haber una solución única, infinitas o ninguna.
Ejemplo
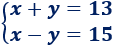
La solución de este sistema de ecuaciones (conjunto de ecuaciones que comparten incógnitas) es \(x=14\) e \(y = -1\). Esta solución es única y verifica AMBAS ecuaciones.
Nota: suele emplearse la llave para agrupar las ecuaciones de un sistema.
Más ejemplos en sistemas de ecuaciones.
3. Ecuación no lineal
Una ecuación es no lineal cuando no es una ecuación lineal. Estas ecuaciones son más complicadas de resolver, sobre todo si tienen más de una incógnita y forman parte de un sistema.
Ejemplo 1
Las ecuaciones de segundo grado son un ejemplo de ecuaciones no lineales con una sola incógnita (\(x\)). Estas ecuaciones tienen la forma (con \(a\neq 0\))
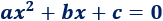
Podemos calcular la o las soluciones mediante la fórmula
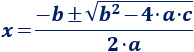
Más ejemplos en ecuaciones de segundo grado.
Ejemplo 2
Las ecuaciones bicuadradas son otro ejemplo de ecuaciones no lineales con una sola incógnita (\(x\)). Estas ecuaciones tienen la forma (con \(a\neq 0\))
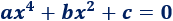
En ecuaciones bicuadradas se explica cómo resolverlas.
Ejemplo 3
Las ecuaciones irracionales son ecuaciones en las que la incógnita se encuentra dentro de una raíz. Por ejemplo,
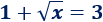
La solución de esta ecuación es \(x=4\). Más ejemplos en ecuaciones bicuadradas.
Ejemplo 4
Las ecuaciones exponenciales son ecuaciones no lineales en las que la incógnita se halla en exponentes. Por ejemplo,
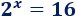
La solución de esta ecuación es \(x = 4\). Más ejemplos en ecuaciones exponenciales.
4. Problemas resueltos
Problema 1
Determinar cuál o cuáles de las siguientes ecuaciones sí son lineales:
- \( x-3xy+ 1 = 0\)
- \( 3x-4y-2 =0\)
- \( x^2+3x=0\)
- \( 1+\log(x) = 2\)
- \( 2x+\sqrt{x} = y\)
- \( 2x+3y+1 = 0\)
- \( x\cdot (2x+y) = 1\)
- \( x+y=2(y-x)\)
- \( (x+y)^2 = 2x+y\)
- \( 2x-z = 3y\)
Solución:
- La ecuación \( x-3xy+ 1 = 0\) no es lineal porque las incógnitas se multiplican entre sí.
- La ecuación \( 3x-4y-2 =0\) es lineal.
- La ecuación \( x^2+3x=0\) no es lineal porque hay una incógnita al cuadrado.
- La ecuación \( 1+\log(x) = 2\) no es lineal porque la incógnita está en un logaritmo.
- La ecuación \( 2x+\sqrt{x} = y\) no es lineal porque la incógnita está en una raíz.
- La ecuación \( 2x+3y+1 = 0\) sí es lineal.
- La ecuación \( x\cdot (2x+y) = 1\) no es lineal porque, si desarrollamos el producto, tenemos \(x^2\) y \(x\cdot y\).
- La ecuación \( x+y=2(y-x)\) sí es lineal.
- La ecuación \( (x+y)^2 = 2x+y\) no es lineal porque, si desarrollamos el cuadrado, tenemos \(x^2\), \(y^2\) y \(2\cdot x\cdot y\).
- La ecuación \( 2x-z = 3y\) sí es lineal.
Problema 2
Resolver la siguiente lineal con 1 incógnita:

Solución:
Esta ecuación es de primer grado y sabemos resolverla:
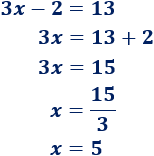
La solución de la ecuación es \(x = 5\).
Problema 3
Buscar \(2\) de las infinitas soluciones de la siguiente ecuación lineal con 2 incógnitas:
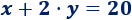
Solución:
Podemos aislar una incógnita y dar valores a la otra para obtener soluciones.
Aislamos la \(x\):
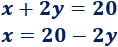
Damos valores a \(y\):
- Si \(y = 0\), entonces

- Si \(y = 1\), entonces
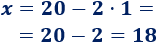
Por tanto, una solución de la ecuación es \(x = 20\) e \(y = 0\) y otra solución es \(x = 18\) e \(y = 1\).
Observad que hay infinitas soluciones.
Problema 4
Buscar \(2\) de las infinitas soluciones de la siguiente ecuación NO lineal:
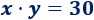
Solución:
Aislamos la \(x\):
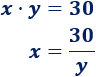
Ahora, damos valores a \(y\), aunque lógicamente \(y\) no debe ser \(0\), ya que no podemos dividir entre \(0\):
- Si \(y = 2\), entonces
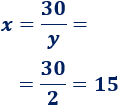
- Si \(y =5\), entonces
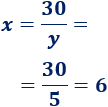
Por tanto, \(x = 15\) e \(y = 2\) es una solución y \(x = 6\) e \(y = 5\) es otra solución.
Problema 5
Sea el sistema de ecuaciones lineales
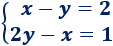
Determinar cuál de las siguientes opciones es la ÚNICA solución del sistema de ecuaciones.
- \(x = 3\) e \(y = 1\).
- \(x = 5\) e \(y = 3\).
- \(x = 0\) e \(y = -2\).
Solución:
Comprobamos las posibles soluciones sustituyendo en las ecuaciones.
- a. \(x = 3\) e \(y = 1\):
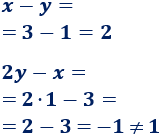
- Cumple la primera ecuación, pero la segunda no. No es solución del sistema.
- b. \(x = 5\) e \(y = 3\):
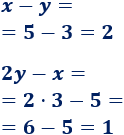
- Cumple ambas ecuaciones, así que sí es solución del sistema.
- c. \(x = 0\) e \(y = -2\):
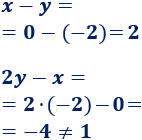
- Sólo cumple una de las ecuaciones, así que no es solución.
Otros temas relacionados:
- Ecuaciones de primer grado
- Ecuaciones de segundo grado
- Ecuaciones bicuadradas
- Sistemas de ecuaciones
- Ecuaciones irracionales
- Ecuaciones exponenciales
- Regla de los signos
- Ecuación de la circunferencia
- Área del círculo
- Perímetro
- ¿Qué es una ecuación?
- ¿Todas las ecuaciones tienen solución?
- ¿Cuántas soluciones tiene una ecuación?
- ¿Hay ecuaciones sin solución?
- ¿Por qué se dice al cuadrado y al cubo?
- Pasar de un lado a otro de la igualdad
Problemas y Ecuaciones ©
ISSN 2659-9899