Ecuaciones irracionales
En esta página explicamos qué es una ecuación irracional y proporcionamos varios métodos para su resolución y 10 ecuaciones resueltas.
Índice:
- ¿Qué es una ecuación irracional?
- Método de elevación
- Método de sustitución
- Más ecuaciones irracionales resueltas
Más ejemplos en ecuaciones irracionales.
1. ¿Qué es una ecuación irracional?
Una ecuación irracional (o ecuación con radicales) es una ecuación en la que la incógnita aparece en el radicando de una o más raíces.
Por ejemplo,
-
La siguiente ecuación tiene la única solución \(x = 4\):
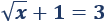
-
La siguiente ecuación tiene las soluciones \(x = 0\) y \(x=-1\):
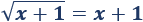
Valores admisibles:
Recordad que el radicando de las raíces de orden par (raíz cuadrada, cuarta, sexta…) tiene que ser siempre no negativo. Por tanto, normalmente, las posibles soluciones pertenecen a un intervalo más pequeño que \(\mathbb{R}\).
Por ejemplo, en la siguiente ecuación, las posibles soluciones deben cumplir \(x \geq 1\):

Es importante considerar los valores admisibles antes de resolver una ecuación.
A continuación, proporcionamos dos métodos para la resolución de ecuaciones irracionales, aunque recomendamos el primero por su sencillez.
2. Método de elevación
Uno de los métodos más sencillos consiste en la elevación sucesiva de ambos lados de la ecuación. Normalmente, escogemos la potencia que hace que desaparezcan las raíces (por ejemplo, elevamos al cuadrado si hay raíces cuadradas).
Ejemplo 1
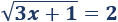
Como el radicando no puede ser negativo, debe cumplirse \(3x+1 \geq 0\). Es decir, \(x \geq -1/3\).
Como la raíz única raíz que aparece es cuadrada, elevamos ambos lados de la ecuación al cuadrado y ésta desaparece:
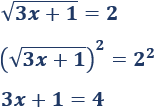
La solución de la ecuación obtenida es \(x=1\). Como esta solución es mayor que \(-1/3\), es la solución de la ecuación irracional.
Ejemplo 2
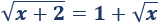
Los valores admisibles para la solución son \(x> 0\).
Como tenemos raíces cuadradas, elevamos al cuadrado:
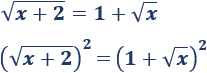
Observad que tenemos el cuadrado de una suma en el lado derecho:
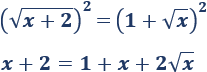
Operamos:
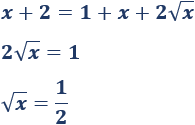
Elevamos de nuevo al cuadrado:
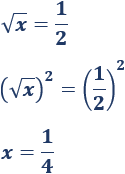
Como la solución obtenida es mayor que \(0\), es la solución de la ecuación irracional inicial.
Consejo
Cuando utilizamos este método (elevación), es recomendable comprobar las soluciones sustituyendo en la ecuación inicial.
3. Método de sustitución
Otra forma de resolver estas ecuaciones es sustituir algunos términos de la ecuación.
Ejemplo
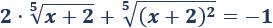
No hay restricciones sobre las posibles soluciones (porque las raíces son de orden impar).
Si elevamos ambos lados a \(5\), tenemos que desarrollar la potencia quinta de una suma. Es más sencillo aplicar el siguiente cambio de variable:
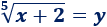
Entonces,
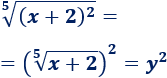
Sustituimos en la ecuación:
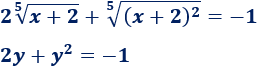
Resolvemos la ecuación de segundo grado obtenida:
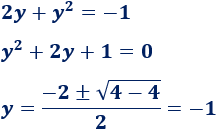
Deshacemos el cambio de variable:
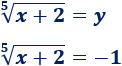
Elevamos a la quinta y resolvemos:
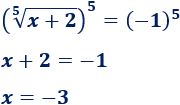
Por tanto, la solución de la ecuación irracional es \(x=-3\).
4. Más ecuaciones irracionales resueltas
Ecuación irracional 1
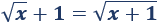
Solución:
Los valores admisibles para las soluciones son los reales no negativos (\(x≥ 0\)).
Elevamos ambos lados al cuadrado:
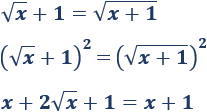
Simplificamos y resolvemos:
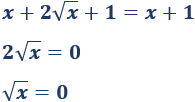
Elevando al cuadrado, tenemos la única solución: \(x=0\).
Ecuación irracional 2
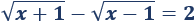
Solución:
Las posibles soluciones deben ser \(x ≥ 1\).
Es más rápido si dejamos una raíz en cada lado para elevar al cuadrado:
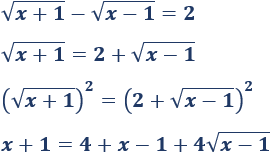
Simplificamos:
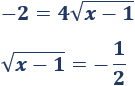
No es necesario continuar porque una raíz cuadrada nunca puede tener como resultado un número negativo. Por tanto, la ecuación irracional no tiene soluciones reales.
Nota: si continuamos elevando al cuadrado, obtenemos la solución \(x=5/4\), que es mayor que \(1\). Sin embargo, si sustituimos en la solución inicial, tenemos que no se cumple la igualdad. Por esta razón, es recomendable comprobar las soluciones.
Ecuación irracional 3
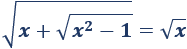
Solución:
Las posibles soluciones deben ser mayores o iguales que \(1\).
Elevamos al cuadrado:
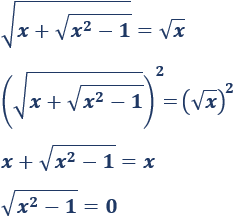
Elevamos al cuadrado de nuevo:
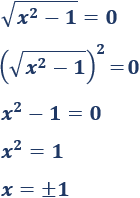
La ecuación obtenida tiene dos soluciones: \(x=1\) y \(x=-1\). Sin embargo, sólo la positiva es solución de la ecuación irracional.
Ecuación irracional 4
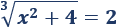
Solución:
Como la raíz es cúbica, cualquier real puede ser solución. Además, observad que el radicando siempre es no negativo.
Elevamos al cubo:
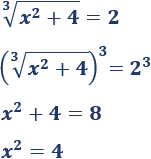
Las soluciones que obtenemos son \(x = 2\) y \(x= -2\). Las dos son soluciones de la ecuación irracional.
Ecuación irracional 5
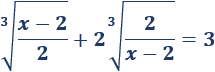
Solución:
La única restricción que tenemos sobre las posibles soluciones es \(x \neq 2\).
Para evitar el desarrollo del cubo de una suma, aplicamos un cambio de variable:
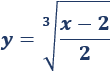
Entonces, la ecuación queda como
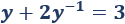
Multiplicamos por \(y\neq 0\):
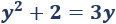
Resolvemos la ecuación:

Las soluciones de la ecuación cuadrática son \(y=1\) e \(y=2\).
Por tanto, por un lado, tenemos
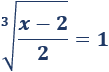
Y por otro,
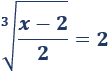
De la primera, obtenemos la solución \(x=4\) y, de la segunda, \(x=18\). Ambas son soluciones de la ecuación irracional.
Ecuación irracional 6

Solución:
Las posibles soluciones deben ser no negativas (por la raíz cuadrada).
Elevamos ambos lados al cubo:
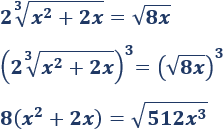
Elevamos ambos lados al cuadrado:
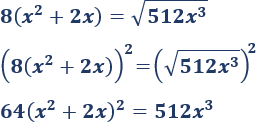
Dividimos ambos lados entre \(64\) y operamos:
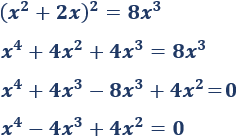
Extraemos factor común:
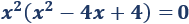
Una solución es \(x=0\).
Resolvemos la ecuación cuadrática:
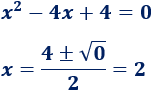
Por tanto, tenemos dos posibles soluciones: \(x=0\) y \(x=2\). Ambas son soluciones de la ecuación irracional puesto que no hacen que el radicando de la raíz cuadrada sea negativo.
Ecuación irracional 7
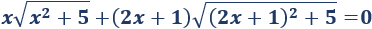
Solución:
Elevando al cuadrado, obtendremos una ecuación de cuarto grado, así que vamos a aplicar un cambio de variable.
Sea la función
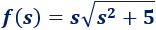
La función \(f\) está definida en todos los reales. Además, es estrictamente creciente, por lo que es inyectiva.
Observad que \(f\) es una función impar, es decir,
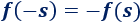
Definimos el siguiente cambio:

Entonces, la ecuación queda como
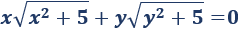
Es decir, tenemos
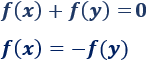
Como la función es impar,
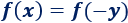
Y como la función es inyectiva,
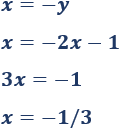
La única solución de la ecuación irracional es \(x = -1/3\).
Más ejemplos en ecuaciones irracionales.