Ecuación de la circunferencia
$$ (x-a)^2 +(y-b)^2 = R^2$$
En esta página proporcionamos la ecuación de la circunferencia de centro (a, b) y radio R, (x-a)²+(y-b)² = R², y de los círculos con y sin borde. Tmabién, resolvemos problemas resueltos relacionados, explicados paso a paso.
Índice:
- Definición de circunferencia
- Ecuación de la circunferencia
- Ecuación del círculo
- Puntos de la circunferencia
- Problemas resueltos
1. Definición de circunferencia
Una circunferencia en el plano se caracteriza por dos elementos: su centro y su radio.
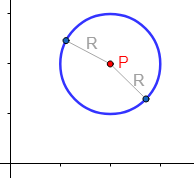
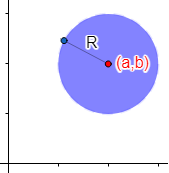
Dado un punto \(P = (a,b)\) del plano, la circunferencia de centro \(P\) y radio \(R\) es el conjunto de puntos situados a una distancia \(R\) de \(P\):
La distancia de cualquier punto de la circunferencia a su centro es exactamente \(R\):
2. Ecuación de la circunferencia
La ecuación de la circunferencia de centro \(P = (a,b)\) y radio \(R\) es
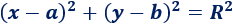
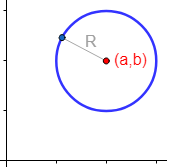
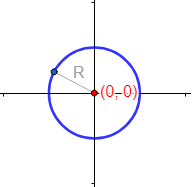
Si el centro es el origen de coordenadas \(P = (0,0)\), la ecuación es más sencilla:
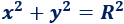
3. Ecuación del círculo
Un círculo es como una circunferencia, pero incluye su interior:
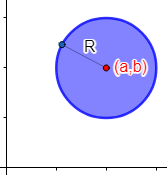
Dado un punto \(P = (a,b)\) del plano, el círculo de centro \(P\) y radio \(R\) es el conjunto de puntos situados a una distancia menor o igual que \(R\) de \(P\).
Por tanto, sólo tenemos que cambiar el signo \(=\) por el signo \(≤\) en la ecuación de la circunferencia:
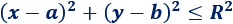
Finalmente, si no queremos el borde del círculo, escribimos el signo de desigualdad estricta:
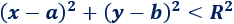
4. Puntos de la circunferencia
Si queremos saber si un punto forma parte de una circunferencia dada (o de un círculo), sólo tenemos que comprobar si sus coordenadas cumplen la ecuación.
Ejemplo
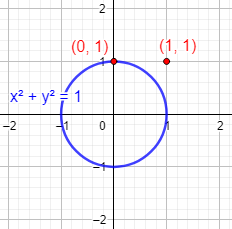
Comprobamos si el punto \((0,1)\) forma parte de la circunferencia \(x^2 +y^2 = 1\):
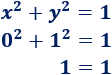
Como el punto verifica la ecuación, está en la circunferencia. Veamos que el punto \((1,1)\) no está en la circunferencia:
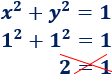
Representación:
5. Problemas resueltos
Problema 1
Escribir la ecuación de la circunferencia de centro (1, 2) y de radio 2.
Solución:
Aplicando la fórmula, la ecuación es de la circunferencia es

Problema 2
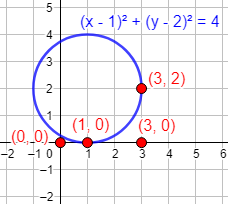
Comprobar si los siguientes puntos pertenecen a la circunferencia del problema anterior: (0, 0), (1, 0), (3, 0), y (3, 2).
Solución:
Tenemos que comprobar si las coordenadas verifican la ecuación.
Punto (0, 0):
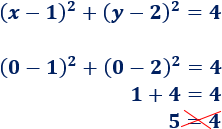
Este punto no está en la circunferencia.
Punto (1, 0):
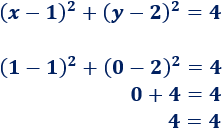
Este punto sí está en la circunferencia.
Punto (3, 0):
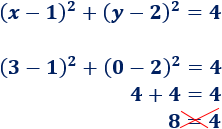
Este punto no está en la circunferencia.
Punto (3, 2):
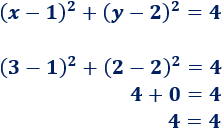
Este punto sí está en la circunferencia.
Representación gráfica:
Problema 3
¿Cuál es el radio y el centro de la siguiente circunferencia?
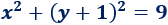
Solución:
Teniendo en cuenta la fórmula, el centro de la circunferencia es el punto (0, -1) y el radio es 3.
Problema 4
Escribir la ecuación del círculo cuyo borde es la circunferencia de radio 2 y centro (1, -1).
Solución:
La ecuación de la circunferencia es

Por tanto, la ecuación del círculo que buscamos es

Problema 5
Problema difícil
¿La siguiente ecuación es la ecuación de una circunferencia? En caso afirmativo, ¿cuál es su centro y radio?
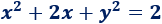
Solución:
Recordamos la ecuación de la circunferencia:
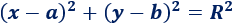
Tenemos que pensar los valores de \(a\), \(b\) y \(R^2\) para que la ecuación coincida con la del problema.
Si desarrollamos los cuadrados, tenemos
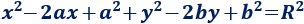
Como en la ecuación del problema sólo aparece una \(y\) (al cuadrado), sabemos que \(b=0\). Por tanto,
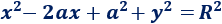
En la ecuación del problema tenemos el sumando \(2x\), así que podemos afirmar que \(a = -1\). Por tanto,
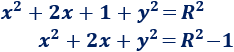
Comparamos esta ecuación con la del problema:
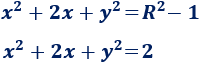
Finalmente, tenemos la relación
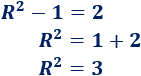
Por tanto, podemos reescribir la ecuación como
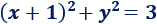
Se trata de la ecuación de la circunferencia de centro (-1,0) y radio \(\sqrt{3}\).