Inecuaciones con valor absoluto
Índice:
- Valor absoluto
- Inecuaciones fáciles
- Inecuaciones difíciles
Explicamos cómo resolver inecuaciones con valores absolutos. Empezamos por inecuaciones fáciles y aumentamos la dificultad poco a poco.
Antes que nada, recordamos el concepto de valor absoluto y resolvemos una ecuación con valor absoluto.
Recomendamos las inecuaciones básicas.
1. Valor absoluto
El valor absoluto de \(a\) es \(|a|\).
El argumento de un valor absoluto es su contenido. El argumento de \(|a|\) es \(a\).
El resultado del valor absoluto es su argumento, pero con signo positivo.
Podemos definir el valor absoluto como
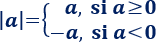
Ejemplo 1
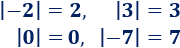
A continuación, resolvemos una ecuación con valor absoluto:
Ejemplo 2
Teniendo en cuenta la definición que vimos,
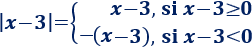
Es decir,
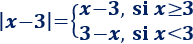
Por tanto, la ecuación del ejemplo ( \(|x-3|=2\) ), se divide en dos ecuaciones:
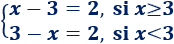
La solución de la primera ecuación es \(x=5\). Es una solución válida porque cumple la condición \(x≥3\).
La solución de la segunda ecuación es \(x=1\). Es una solución válida porque cumple la condición \(x<3\).
Por tanto, las soluciones de la ecuación \(|x-3|=2\) son \(x=5\) y \(x=1\).
2. Inecuaciones fáciles
En este apartado enunciamos dos propiedades del valor absoluto que nos facilitan la resolución de las inecuaciones con valor absoluto.
Propiedad 1
Si \(K>0\) y tenemos
Entonces, podemos escribir
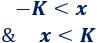
¡Deben cumplirse ambas!
Normalmente, se escribe directamente
Ejemplo 3
Los números que están entre \(0\) y \(3\) verifican la inecuación. Los que están entre \(-3\) y \(0\), también. Por eso, escribimos
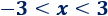
La solución de esta inecuación es
Ejemplo 4
Por la propiedad 1,
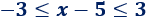
Resolvemos la inecuación de la izquierda:
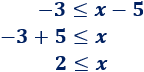
La solución es \(x≥2\).
Resolvemos la de la derecha:
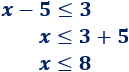
La solución es \(x≤8\).
Como deben cumplirse ambas inecuaciones, la solución de la inecuación inicial es
Ejemplo 5
Aplicamos la propiedad 1:
Obtenemos dos inecuaciones de ésta:
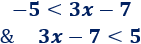
Resolvemos la primera:
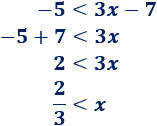
Resolvemos la segunda:
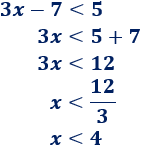
Por tanto, como deben cumplirse ambas inecuaciones, la solución de la inecuación inicial es
Propiedad 2
Si \(K>0\) y tenemos
Entonces, podemos escribir
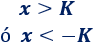
Debe cumplirse una de las condiciones.
Si se trata del signo \(≥\), debe cumplirse una condición o ambas. Se cumplen ambas cuando se da la igualdad.
Ejemplo 6
Las soluciones de esta inecuación son las \(x\) mayores que \(1\) y las menores que \(-1\). Por ejemplo,
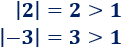
Ejemplo 7
Por la propiedad 2, tenemos dos inecuaciones:
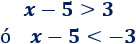
Las soluciones de la primera son \(x>8\). Las de la segunda son \(x<2\).
Por tanto, las soluciones de la inecuación inicial son
3. Inecuaciones difíciles
Complicamos un poco las inecuaciones.
Ejemplo 8
Por la propiedad 2,
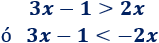
Resolvemos la primera inecuación:
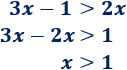
Resolvemos la segunda:
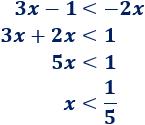
Como no es necesario que se verifiquen las dos inecuaciones simultáneamente, la solución de la inecuación inicial es
Ejemplo 9
Por la propiedad 2,
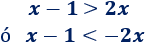
Resolvemos la primera inecuación:
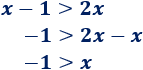
Resolvemos la segunda:
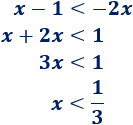
La solución de la inecuación inicial es la unión de ambas soluciones:
Observad que es lo mismo que
Ejemplo 10
Por la propiedad 1,
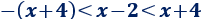
Es decir,
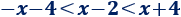
Resolvemos la inecuación de la izquierda:
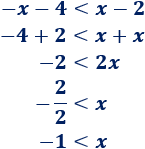
Resolvemos la de la derecha:
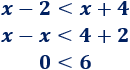
La desigualdad \(0<6\) es siempre verdadera. Esto significa que cualquier \(x\) cumple esta inecuación.
Como la solución de la inecuación inicial debe cumplir ambas, es
Ejemplo 11
Por la propiedad 1,
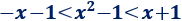
Resolvemos la inecuación de la izquierda:
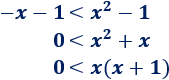
Queremos que el polinomio \(x^2+x\) sea positivo. Sabemos que es \(0\) cuando \(x=0\) o cuando \(x=-1\).
- Si \(x<-1\), el polinomio es positivo.
- Si \(-1<x<0\), es negativo.
- Si \(x>0\), es positivo.
La solución de esta inecuación es
Resolvemos la inecuación de la derecha:
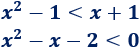
El polinomio debe ser negativo. Es cero cuando \(x=-1\) ó \(x=2\).
- Si \(x<-1\), es positivo.
- Si \(-1<x<2\), es negativo.
- Si \(x>2\), es positivo.
La solución de esta inecuación es
La solución de la inecuación es la intersección de las soluciones de ambas inecuaciones. Por tanto, su solución es
Ejemplo 12
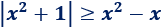
Por la propiedad 2,
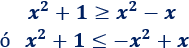
Resolvemos la primera inecuación:
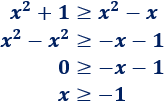
Resolvemos la segunda:
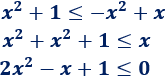
Esta inecuación no tiene soluciones puesto que la función \(y=2x^2-x+1\) es una parábola con forma de \(\cup\) que no tiene raíces (no corta el eje OX). Por tanto, siempre es positivo.
La solución de la inecuación inicial es
Más inecuaciones resueltas:
- Inecuaciones básicas
- Inecuaciones lineales, de segundo grado y racionales
- Inecuaciones con valor absoluto