¿Qué son las ecuaciones equivalentes?
En esta página explicamos qué son las ecuaciones equivalentes, su importancia, cómo obtenerlas y sus aplicaciones. Con ejemplos y problemas resueltos.
Índice:
- Ecuaciones equivalentes
- Operaciones elementales
- Aplicación para la resolución de ecuaciones
- Multiplicar/dividir por la incógnita
- Alusión a los sistemas de ecuaciones
- Problemas resueltos
1. Ecuaciones equivalentes
Dos ecuaciones son equivalentes cuando la solución (o soluciones) de ambas ecuaciones es la misma.
Ejemplos
- La solución de la siguiente ecuación es \(x = 2\):
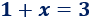
- La solución de la siguiente ecuación también es \(x = 2\):
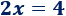
- La solución de la siguiente ecuación también es \(x = 2\):
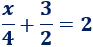
Las ecuaciones del ejemplo anterior son distintas, pero tienen la misma solución, por lo que se dice que son equivalentes. De hecho, a continuación, veremos que podemos pasar de una ecuación a otra equivalente mediante operaciones elementales.
2. Operaciones elementales
Dada una igualdad matemática, una operación es elemental cuando la igualdad se mantiene. Las operaciones elementales son las siguientes.
Sumar/restar en ambos lados de la igualdad
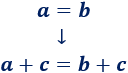
Multiplicar/dividir ambos lados por un número \(c\neq 0\)
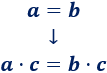
Cambiar un término por otro (sustituir)
Si \(a=h\), podemos cambiar \(a\) por \(h\):
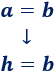
Estas operaciones permiten obtener ecuaciones equivalentes.
Ejemplo
En el ejemplo del apartado anterior vimos que las dos siguientes ecuaciones son equivalentes por tener la misma solución (\(x = 2\)):
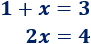
Veamos que podemos pasar de la primera ecuación a la segunda mediante operaciones elementales.
- 1. Restamos \(-1\) en ambos lados:
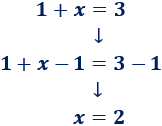
- 2. Multiplicamos ambos lados por el número \(2\):
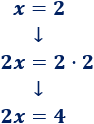
Veamos que también podemos pasar de la ecuación \(1 +x = 3\) a la tercera ecuación del ejemplo, que es
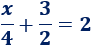
- 1. Restamos \(1\) en ambos lados:
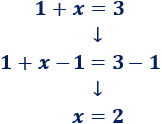
- 2. Dividimos entre \(4\) en ambos lados:
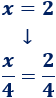
- 3. Sumamos el número \(3/2\) en ambos lados:
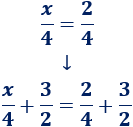
- 4. La suma de las fracciones del lado derecho es \(2\):
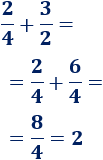
Por tanto, la ecuación resultante es
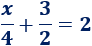
3. Aplicación para la resolución de ecuaciones
Cuando resolvemos una ecuación de primer grado (o una ecuación en general) lo que hacemos es simplificar la ecuación hasta hallar la solución (pasamos sumandos de un lado a otro, eliminamos paréntesis, etc.). Este proceso de simplificar la ecuación es en realidad la obtención de una serie de ecuaciones equivalentes a la inicial con una expresión cada vez más sencilla.
Ejemplo
Sea la ecuación

- 1. Pasamos el \(2\) restando al otro lado:
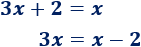
- 2. Pasamos la \(x\) de la derecha restando al otro lado:
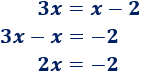
- 3. Pasamos el coeficiente \(2\) de la incógnita dividiendo al otro lado:
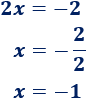
Observad que todas estas operaciones realizadas corresponden a operaciones elementales:
- Restamos \(2\) en ambos lados.
- Restamos \(x\) en ambos lados.
- Dividimos entre \(2\) en ambos lados.
Además, entre estos pasos hemos sumado o restado términos, lo cual equivale a la operación elemental de sustituir términos. Por ejemplo, hicimos el cambio \(-2/2 = -1\).
4. Multiplicar/dividir por la incógnita
La operación de multiplicar o dividir toda la ecuación por la incógnita no es una operación válida para la obtención de ecuaciones equivalentes puesto que se añaden o eliminan, respectivamente, soluciones a la ecuación.
Esto es fácil de ver mediante un ejemplo.
Ejemplo
Consideremos la ecuación de segundo grado
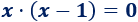
Esta ecuación tiene dos únicas soluciones y son \(x = 0\) y \(x = 1\), ya que
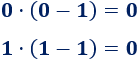
Si dividimos la ecuación inicial entre \(x\), tenemos:
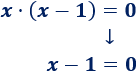
La ecuación \(x-1 = 0\) sólo tiene la solución \(x=1\), así que no es equivalente a la inicial.
Además, nunca podemos dividir entre un valor desconocido (como es \(x\)) ya que \(x\) podría ser \(0\).
Si repetimos el proceso a la inversa, tenemos un ejemplo de adición de soluciones: si multiplicamos la ecuación \(x-1=0\) por \(x\), obtenemos la ecuación \(x\cdot (x-1)=0\), con lo que habremos pasado de una ecuación con una solución (\(x = 1\)) a una ecuación con dos soluciones (\(x=1\) y \(x=0\)).
5. Alusión a los sistemas de ecuaciones
La equivalencia entre ecuaciones es una gran herramienta para la resolución de sistemas de ecuaciones lineales. El álgebra matricial, que facilita dicha tarea, se basa precisamente en este tipo de operaciones elementales entre las ecuaciones del sistema.
Ejemplos y más información:
- Sistemas de ecuaciones
- Eliminación de Gauss (álgebra matricial)
- Teorema de Rouché-Frobenius (álgebra matricial)
- Regla de Cramer (álgebra matricial)
6. Problemas resueltos
Problema 1
Determinar si las siguientes ecuaciones son equivalentes:
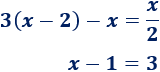
Solución:
Una forma de resolver el problema es pasar de una ecuación a la otra mediante operaciones elementales, pero como ya hemos visto este proceso en los ejemplos anteriores, razonaremos de un modo distinto.
Ambas ecuaciones son de primer grado, es decir, sólo hay una incógnita y no tiene exponente. Esto significa que tienen una única solución, infinitas o ninguna.
La solución de la segunda ecuación es \(x = 4\):
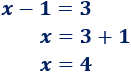
Si las ecuaciones son equivalentes, deben tener la misma solución. Comprobamos si \(x=4\) es solución de la primera ecuación (sustituyendo \(x\) por \(4\)):
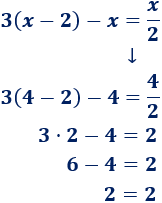
Por tanto, \(x = 2\) sí es solución de la primera ecuación.
Ahora bien, para asegurar que son ecuaciones equivalentes, debemos comprobar que la primera ecuación no tiene infinitas soluciones. Si las tuviera, \(x=0\) sería una de ellas. Comprobamos que no es así:
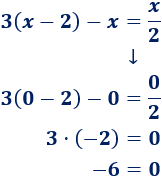
Problema 2
¿Son equivalentes las siguientes ecuaciones?
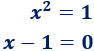
Solución:
No, no pueden serlo:
- La primera ecuación es una ecuación de segundo grado y, por tanto, tiene dos soluciones, que son \(x =1\) y \(x = -1\).
- La segunda ecuación es una ecuación de de primer grado y tiene una única solución: \(x = 1\).
Si fueran ecuaciones equivalentes, tendrían el mismo número de soluciones (y las mismas soluciones).
Problema 3
¿Son equivalentes las siguientes ecuaciones?
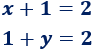
Solución:
Sí son equivalentes, puesto que la solución es la misma: \(1\). El hecho de que la incógnita se llame \(x\) o se llame \(y\) es irrelevante.
De hecho, podemos obtener una ecuación a partir de la otra:
- 1. Restamos \(1\) en la primera ecuación:
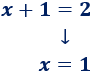
- 2. Restamos \(1\) en la segunda ecuación:
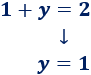
- 3. Finalmente, como \(y = 1\) y \(x = 1\), podemos sustituir \(x\) por \(y\) en ambas ecuaciones:
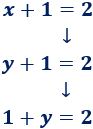
Otros temas relacionados:
- Cálculo de límites
- Indeterminación 0/0
- Límites e indeterminaciones
- ¿Qué es una ecuación?
- ¿Todas las ecuaciones tienen solución?
- ¿Cuántas soluciones tiene una ecuación?
- ¿Hay ecuaciones sin solución?
- ¿Por qué se dice al cuadrado y al cubo?
- Pasar de un lado a otro de la igualdad
Problemas y Ecuaciones ©
ISSN 2659-9899