Método de Eliminación de Gauss
En esta página vamos a explicar el método de eliminación de Gauss mientras resolvemos 4 sistemas de 3 ecuaciones lineales con 3 incógnitas (uno de cada tipo y otro extra).
Nota: para reducir el texto, consideramos que ya sabemos qué es un sistema de ecuaciones lineales.
Índice de contenidos:
- Tipos de sistemas
- Forma matricial de un sistema
- Método de eliminación de Gauss
- Sistemas resueltos por eliminación de Gauss
1. Tipos de sistemas
Un sistema de ecuaciones lineales puede ser:
-
Compatible determinado: sólo tiene una solución.
-
Compatible indeterminado: tiene infinitas soluciones.
-
Incompatible: no tiene solución.
2. Forma matricial de un sistema
La forma matricial de un sistema de ecuaciones lineales es

donde
-
\(A\) es la matriz que en la fila \(k\) contiene los coeficientes de las incógnitas de la ecuación \(k\).
-
\(X\) es la matriz columna con las incógnitas.
-
\(B\) es la matriz columna con los términos independientes de las ecuaciones.
-
\(A^*\) es la matriz ampliada o aumentada del sistema, formada por las matrices \(A\) y \(B\):
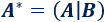
Ejemplo
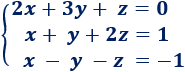
Se trata de un sistema con 3 ecuaciones lineales y 3 incógnitas.
Su forma matricial es
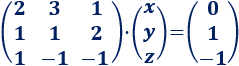
Y su matriz ampliada o aumentada es
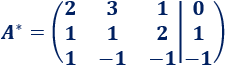
Observad que un sistema queda determinado por su matriz ampliada (o cualquier matriz equivalente a ésta).
3. Método de eliminación de Gauss
Recordad que para resolver un sistema de ecuaciones podemos, sin alterar las soluciones del sistema:
-
Intercambiar el orden de las ecuaciones.
-
Sumar algunas de sus ecuaciones.
-
Multiplicar alguna ecuación por un número distinto de 0.
Esto es precisamente lo que se hace en el método de Gauss: se modifican las ecuaciones para obtener un sistema mucho más fácil de resolver, pero, en lugar de hacerlo sobre las ecuaciones, se hace sobre la matriz ampliada del sistema.
Ejemplo
Si multiplicamos por 2 todas las ecuaciones del ejemplo anterior, tenemos el sistema
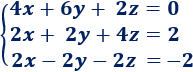
La matriz ampliada de este sistema es
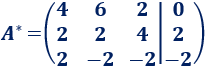
Es decir, es la matriz ampliada del ejemplo anterior pero multiplicada por 2.
Obviamente, multiplicar todas las ecuaciones por 2 no sirve de mucha ayuda. Lo que queremos dar a entender es que realizar operaciones entre las filas de la matriz ampliada es lo mismo que realizarlas sobre las ecuaciones del sistema.
El método de eliminación de Gauss consiste en operar sobre la matriz ampliada del sistema hasta hallar la forma escalonada (una matriz triangular superior). Así, se obtiene un sistema fácil de resolver por sustitución hacia atrás.
Si finalizamos las operaciones al hallar la forma escalonada reducida (forma lo más parecida a la matriz identidad), entonces el método se denomina eliminación de Gauss-Jordan.
En los ejemplos veremos que una vez terminado el proceso, resolver el sistema es directo. Además de esto, veremos que
-
Si se obtiene la matriz identidad, el sistema es compatible determinado (como en el sistema 1).
-
Si se obtiene alguna fila de ceros con término independiente distinto de 0, el sistema es incompatible (como en el sistema 2).
-
Si se obtiene alguna fila de ceros y no estamos en el caso anterior, el sistema es compatible indeterminado (como en el sistema 3).
Nota: La clasificación de los sistemas según la forma escalonada de su matriz ampliada se deduce del teorema de Rouché-Frobenius.
4. Sistemas resueltos por Gauss
Nota: durante el método, seguiremos llamando \(A^*\) a las matrices obtenidas porque son equivalentes a la matriz ampliada inicial.
Sistema 1
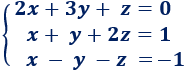
Solución:
La matriz ampliada del sistema es
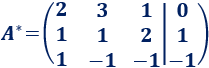
A fila 1 le restamos dos veces la fila 3 y a la fila 2 le restamos la fila 3:
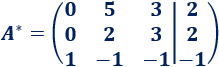
A la fila 1 le restamos la fila 2:
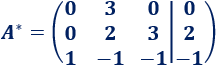
Dividimos la fila 1 entre 3:

A la fila 3 le sumamos la fila 1 y a la fila 2 le restamos dos veces la fila 1:

Dividimos la fila 2 entre 3:

A la fila 3 le sumamos la fila 2:
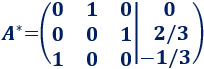
Reordenamos las 3 filas:
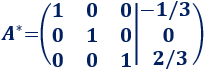
Ya tenemos resuelto el sistema porque la matriz obtenida es la solución:
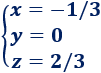
El sistema es compatible determinado.
Sistema 2
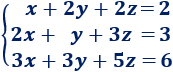
Solución:
La matriz ampliada del sistema es
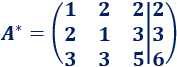
A la fila 2 le restamos dos veces la fila 1 y a la fila 3 le restamos tres veces la fila 1:
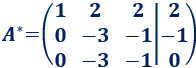
A la fila 3 le restamos la fila 2:
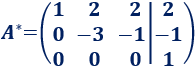
El sistema es incompatible (no tiene solución) porque la tercera fila representa la ecuación imposible o igualdad falsa:
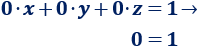
Sistema 3
Solución:
La matriz ampliada del sistema es
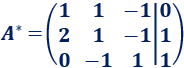
Sumamos a las filas 1 y 2 la fila 3:

A la fila 2 le restamos dos veces la fila 1:
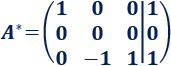
Cambiamos el signo de la fila 3:
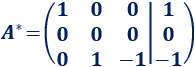
Cuando tenemos una fila de ceros, el sistema no es determinado (hay más incógnitas que ecuaciones). Si el sistema no es incompatible, entonces es indeterminado.
Tenemos la matriz ampliada del sistema
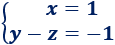
O bien,
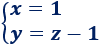
Las soluciones del sistema son
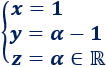
Podéis observar que el sistema tiene infinitas soluciones: para cada valor de \(\alpha\) hay una solución distinta.
Por ejemplo, si \(\alpha = 2\), tenemos la solución
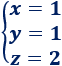
Y si \(\alpha = 3\), tenemos la solución
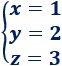
Sistema 4
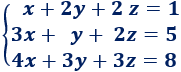
Solución:
La matriz ampliada del sistema es
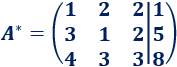
A la fila 2 le restamos tres veces la fila 1:

A la fila 3 le restamos cuatro veces la fila 1:
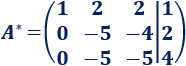
A la fila 3 le restamos la fila 2:
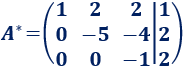
Cambiamos de signo la fila 3:
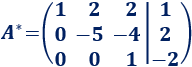
A la fila 2 le sumamos cuatro veces la fila 3:

Dividimos entre -5 la fila 2:

A la fila 1 le restamos dos veces la fila 2:
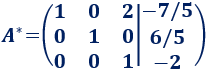
A la fila 1 le restamos dos veces la fila 3:

Por tanto, el sistema es compatible determinado y su solución es
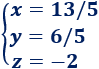
Más ejemplos: sistemas de ecuaciones resueltos por eliminación de Gauss.
Calculadoras de matrices:
- Calculadora para multiplicar matrices
- Calculadora de determinantes
- Calculadora de la matriz inversa
- Calculadora de la regla de Cramer
Más información y problemas resueltos de álgebra matricial: