Potencias enésimas de matrices
En esta página veremos ejemplos de cómo calcular las potencias enésimas de matrices cuadradas de dimensión 2 y 3, aunque el método es el mismo para todas las dimensiones.
Índice de contenidos:
- Introducción
- 5 ejemplos
Introducción
Sólo podemos calcular potencias de matrices cuadradas porque el número de filas debe coincidir con el de filas para poder calcular los productos.
Algunas matrices presentan una especie de patrón en sus potencias. Por ejemplo, sea la matriz
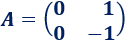
Calculamos su cuadrado:
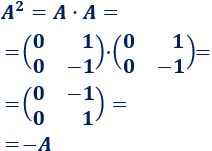
Como \(A^2\) es \(-A\), las potencias de \(A\) forman una secuencia que se repite:
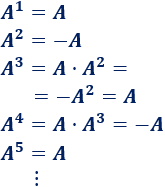
Por tanto, la potencia \(A^n\) es igual a \(A\) si \(n\) es impar y es igual a \(-A \) si \(n\) es par:
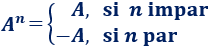
Luego podemos calcular cualquier potencia \(A\) rápidamente con la fórmula dada.
Más ejemplos
Calculad la matríz enésima de las 5 siguientes matrices:
Matriz 1
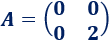
Solución:
Calculamos \(A\) al cuadrado:
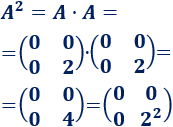
Calculamos \(A\) al cubo:
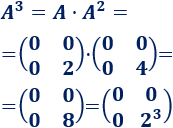
Es fácil ver que la potencia enésima de la matriz \(A\) es
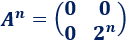
Matriz 2
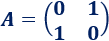
Solución:
Calculamos \(A\) al cuadrado:
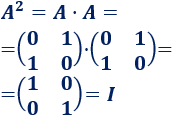
El cuadrado de \(A\) es la matriz identidad. Por tanto, \(A\) al cubo es \(A\):
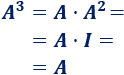
Las potencias de \(A\) dependen de si el exponente es par o impar:
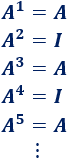
Por tanto, la potencia enésima de \(A\) es
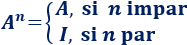
Matriz 3

Solución:
Calculamos \(A\) al cuadrado:
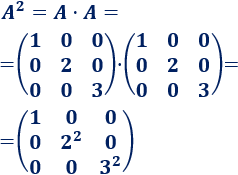
En cada potencia, los exponentes de la diagonal aumentan. Por tanto, la potencia enésima es
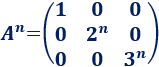
Matriz 4
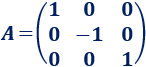
Solución:
Teniendo en cuenta que la matriz es diagonal y que en el problema anterior vimos que los exponentes de la diagonal aumentan en cada potencia, ya podemos asegurar que la potencia enésima de la matriz es
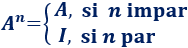
Matriz 5

Solución:
Calculamos \(A\) al cuadrado:
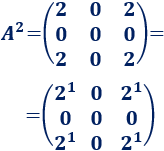
Calculamos \(A\) al cubo:
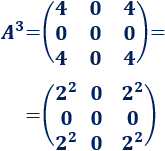
Por tanto, la potencia enésima de la matriz \(A\) es
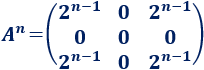
Podéis encontrar más problemas de este tipo en potencias de matrices.
Calculadoras de matrices:
- Calculadora para multiplicar matrices
- Calculadora de determinantes
- Calculadora de la matriz inversa
- Calculadora de la regla de Cramer
Más información y problemas resueltos de álgebra matricial:
- Suma de matrices
- Producto de matrices
- Determinantes de matrices
- Matriz inversa
- Regla de Cramer
- Eliminación de Gauss
- Otros temas de álgebra matricial