Matriz adjunta o de cofactores
En esta página definimos la matriz adjunta o de cofactores y proporcionamos 4 ejemplos de la adjunta de matrices de dimensiones 2x2 y 3x3.
Definición
Sea \(A\) una matriz de dimensión mxm. La matriz adjunta de \(A\), \(A^*\), es una matriz de la misma dimensión. El elemento de la posición fila \(i\) y columna \(j\) de la matriz adjunta de \(A\) (llamado cofactor de la posición \( (i,j) \)) es
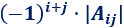
siendo la matriz \(A_{ij}\) la submatriz de \(A\) obtenida al eliminar la fila \(i\) y columna \(j\) de \(A\).
Explicación:
El factor \((-1)^{i+j}\) es 1 si la suma de las posiciones fila y columna es par, y -1 si es impar. Lo que hace este factor es determinar el signo.
Por ejemplo, si \(A\) es de dimensión 2x2:
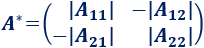
Y, si es de dimensión 3x3:
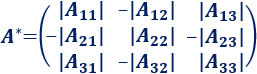
La importancia de la matriz adjunta de una matriz \(A\) se debe a que, si la matriz \(A\) tiene inversa, podemos calcularla a partir de la traspuesta de su adjunta y su determinante mediante la siguiente fórmula:
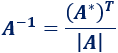
Ejemplos: Cálculo de la matriz inversa.
Ejemplos de matriz adjunta
Ejemplo 1
Matriz de dimensión 2x2
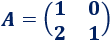
Solución:
Como la matriz es de dimensión 2, los determinantes que tenemos que calcular son de dimensión 1, así que no hay que realizar operaciones.
Calculamos todos los elementos de la matriz adjunta:
El elemento de la posición (1,1) es
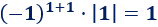
El elemento de la posición (1,2) es

El elemento de la posición (2,1) es
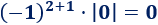
El elemento de la posición (2,2) es

Por tanto, la matriz adjunta de \(A\) es
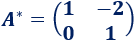
Ejemplo 2
Matriz de dimensión 2x2
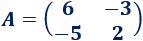
Solución:
Calculamos todos los elementos de la matriz adjunta:
El elemento de la posición (1,1) es
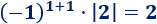
El elemento de la posición (1,2) es
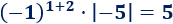
El elemento de la posición (2,1) es
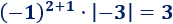
El elemento de la posición (2,2) es

Por tanto, la matriz adjunta de \(A\) es
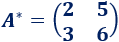
Ejemplo 3
Matriz de dimensión 3x3
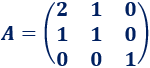
Solución:
Como la matriz es de dimensión 3x3, tendremos que calcular determinantes de dimensión 2x2.
Calculamos los elementos de la matriz adjunta:
El elemento de la posición (1,1) es
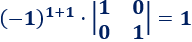
El elemento de la posición (1,2) es
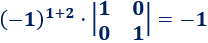
El elemento de la posición (1,3) es
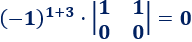
El elemento de la posición (2,1) es
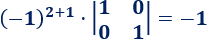
El elemento de la posición (2,2) es
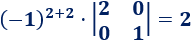
El elemento de la posición (2,3) es
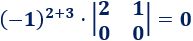
El elemento de la posición (3,1) es
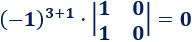
El elemento de la posición (3,2) es
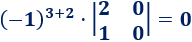
El elemento de la posición (3,3) es
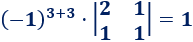
La matriz adjunta es
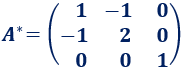
Ejemplo 4
Matriz de dimensión 3x3

Solución:
Calculamos los elementos de la matriz adjunta:
El elemento de la posición (1,1) es
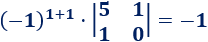
El elemento de la posición (1,2) es
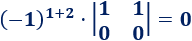
El elemento de la posición (1,3) es
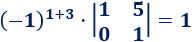
El elemento de la posición (2,1) es
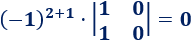
El elemento de la posición (2,2) es
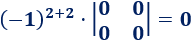
El elemento de la posición (2,3) es
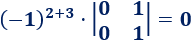
El elemento de la posición (3,1) es
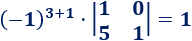
El elemento de la posición (3,2) es
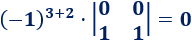
El elemento de la posición (3,3) es
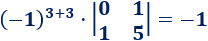
La matriz adjunta es
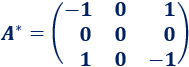
Calculadoras de matrices:
- Calculadora para multiplicar matrices
- Calculadora de determinantes
- Calculadora de la matriz inversa
- Calculadora de la regla de Cramer
Más información y problemas resueltos de álgebra matricial:
- Suma de matrices
- Producto de matrices
- Determinantes de matrices
- Matriz inversa
- Regla de Cramer
- Eliminación de Gauss
- Otros temas de álgebra matricial