Cálculo de la matriz inversa
En esta página vamos a explicar los dos métodos más utilizados para calcular la matriz inversa:
- Método de Gauss
- Método de la adjunta
Índice de contenidos:
- Introducción
- Inversa mediante Gauss
- Inversa mediante la adjunta
- Más ejemplos
Enlace: Calculadora online de la matriz inversa
Introducción
Recordad que si \(A\) es una matriz cuadrada de dimensión \(nxn\) y es regular (su determinante es distinto de 0), entonces existe una matriz llamada matriz inversa de \(A\), \(A^{-1}\), tal que
-
\(A^{-1}\) es de dimensión \(nxn\)
-
\(A^{-1}\) es el inverso multiplicativo de \(A\) por ambos lados, es decir,
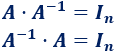
siendo \(I_n\) la matriz identidad de dimensión \(nxn\)
-
Su determinante es
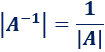
- \(A^{-1}\) es única, es decir, es la única matriz que cumple las igualdades del segundo punto.
Inversa mediante Gauss
Dada una matriz \(A\) cuadrada de dimensión \(nxn\) y regular, definimos la matriz por bloques formada por la matriz \(A\) y la matriz \(I_n\) (matriz identidad de dimensión \(nxn\)):

Por ejemplo, si A es dimensión 2x2,
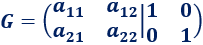
Y si es de dimensión 3x3,
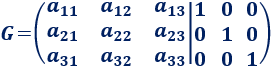
Para calcular la matriz inversa de \(A\), se realizan operaciones elementales fila para conseguir la forma escalonada reducida de la matriz \(G\).
Dicho en otras palabras, se realizan operaciones elementales filas hasta conseguir la matriz identidad en el bloque izquierdo de la matriz \(G\), es decir,
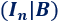
Al terminar las operaciones, la matriz identidad que había en el lado derecho se ha transformado en otra matriz \(B\). Esta matriz \(B\) es precisamente la matriz inversa de \(A\).
Ejemplo
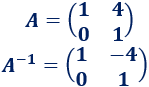
Construimos la matriz por bloques:
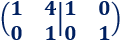
Para obtener la matriz identidad en el bloque izquierdo sólo tenemos que restarle a la fila 1 cuatro veces la fila 2:
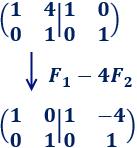
Como ya tenemos la identidad en el bloque izquierdo, la matriz del bloque derecho es la inversa:
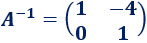
Inversa mediante la adjunta
En este método tenemos que aplicar la fórmula
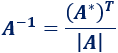
Es decir, la matriz inversa de \(A\) es la matriz transpuesta de la matriz adjunta dividida entre el determinante de \(A\).
Nota: hemos llamado \(A^*\) a la matriz adjunta de \(A\). A veces, también se utiliza \(A^*\) para denotar la matriz ampliada de un sistema de ecuaciones.
Recordad que la matriz adjunta de \(A\) tiene la misma dimensión que \(A\) y se calcula con determinantes de submatrices:
El elemento de la posición fila \(i\) y columna \(j\) de la matriz adjunta de \(A\) es
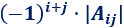
siendo la matriz \(A_{ij}\) la submatriz de \(A\) obtenida al eliminar la fila \(i\) y columna \(j\) de \(A\).
Ejemplo
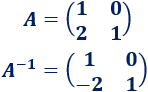
Calculamos el determinante de la matriz \(A\):
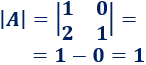
Calculamos la matriz adjunta de \(A\). Como su dimensión es 2x2, tenemos que calcular determinantes de dimensión 1.
El elemento de la posición (1,1) es
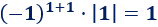
El elemento de la posición (1,2) es

El elemento de la posición (2,1) es
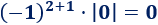
El elemento de la posición (2,2) es

Por tanto, la matriz adjunta de \(A\) es
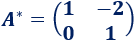
Calculamos su traspuesta (cambiando filas por columnas):
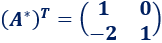
Calculamos la inversa:
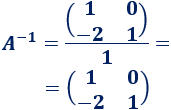
Más ejemplos
Matriz 1
Calcular la inversa de \(A\) mediante Gauss:

Solución:
Construimos la matriz por bloques:

Restamos a la fila 2 el doble de la fila 1:
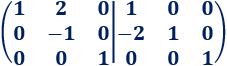
Sumamos a la fila 1 el doble de la fila 2:
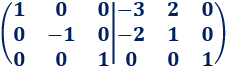
Multiplicamos la fila 2 por -1:
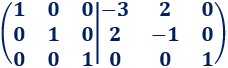
Ya hemos terminado porque tenemos la identidad en el lado izquierdo. Por tanto, la inversa de \(A\) es
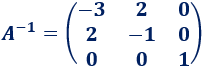
Matriz 2
Calcular la inversa de \(A\) mediante su adjunta:
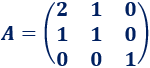
Solución:
Calculamos el determinante de \(A\):
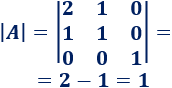
Calculamos la matriz adjunta de \(A\).
El elemento de la posición (1,1) es
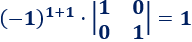
El elemento de la posición (1,2) es
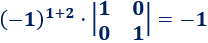
El elemento de la posición (1,3) es
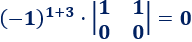
El elemento de la posición (2,1) es
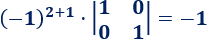
El elemento de la posición (2,2) es
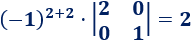
El elemento de la posición (2,3) es
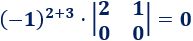
El elemento de la posición (3,1) es
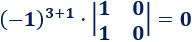
El elemento de la posición (3,2) es
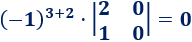
El elemento de la posición (3,3) es
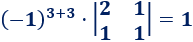
La matriz adjunta es
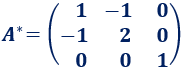
Su traspuesta es
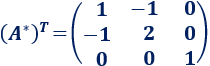
Nota: la matriz \(A^*\) es simétrica (es igual a su traspuesta).
Por tanto, la matriz inversa de \(A\) es

Matriz 3
Calcular la inversa de la siguiente matriz diagonal:
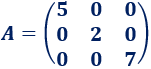
Solución:
Si calculamos la inversa mediante la adjunta, tenemos que calcular muchos determinantes. Como la matriz ya es casi la identidad, es más rápido aplicar el método de Gauss:

Sólo tenemos que dividir entre 5 la fila 1, entre 2 la fila 2 y entre 7 la fila 3:
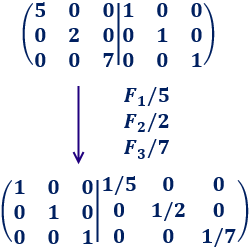
Por tanto, la inversa de \(A\) es
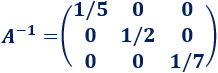
Nota: la matriz inversa de una matriz diagonal regular \(A\) es una matriz diagonal cuyos elementos de la diagonal son los inversos de los de \(A\).
Más ejemplos:
Calculadoras de matrices:
- Calculadora para multiplicar matrices
- Calculadora de determinantes
- Calculadora de la matriz inversa
- Calculadora de la regla de Cramer
Más información y problemas resueltos de álgebra matricial:
- Suma de matrices
- Producto de matrices
- Determinantes de matrices
- Matriz inversa
- Regla de Cramer
- Eliminación de Gauss
- Otros temas de álgebra matricial