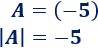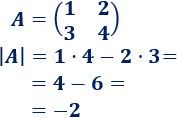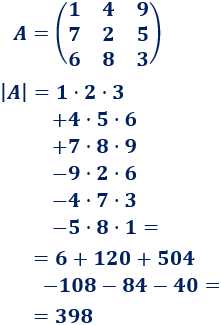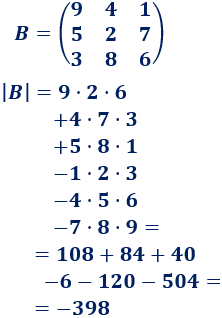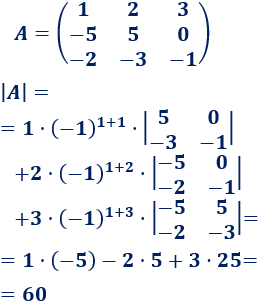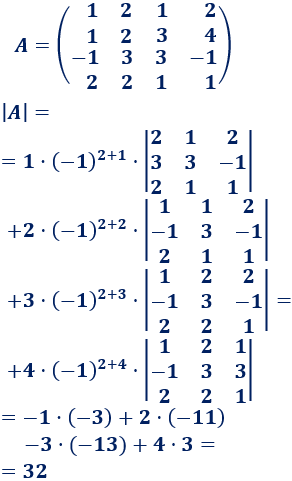Determinantes de matrices
En esta página vamos a explicar cómo se calculan los determinantes de matrices cuadradas de todas las dimensiones.
Índice de contenidos:
- Introducción
- Dimensión 1x1
- Dimensión 2x2
- Dimensión 3x3 (Regla de Sarrus)
- Regla de Laplace
Introducción
El determinante de matrices de dimensión menor que 4 se calcula rápidamente mediante reglas o fórmulas. Para dimensiones mayores, es necesario desarrollar el determinante mediante otros métodos. Nosotros veremos la llamada regla de Laplace.
Notas previas:
-
Como las matrices deben ser cuadradas, tienen el mismo número de filas que de columnas.
-
Para denotar el determinante de una matriz \(A\), usamos \(|A|\) ó \(det(A)\).
-
Escribiemos \(a_{ij}\) para referirnos al elemento de la fila \(i\) y columna \(j\) de la matriz \(A\).
Enlace: calculadora online de determinantes 2x2, 3x3 y 4x4.
Dimensión 1x1
Una matriz de dimensión 1x1 tiene la forma
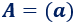
El determinante de \(A\) es el único elemento de la matriz:
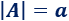
Dimensión 2x2
Las matrices de dimensión 2x2 tienen la forma
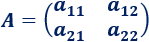
Su determinante es
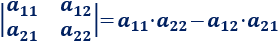
Regla mnemotécnica: multiplicamos en las diagonales y las restamos.
Dimensión 3x3 (Regla de Sarrus)
Las matrices de dimensión 3x3 tienen la forma

Su determinante se calcula mediante la llamada regla de Sarrus:

Regla mnemotécnica: la regla de Sarrus parece complicada, pero si os fijáis bien, también estamos multiplicando diagonales. Observando los siguientes dos ejemplos, os quedará más claro:
Regla de Laplace
La regla o desarrollo de Laplace permite calcular el determinante de matrices cuadradas de cualquier dimensión, pero normalmente se utiliza para dimensión mayor que 3.
Existen dos versiones de la regla: desarrollo por filas y desarrollo por columnas.
Desarrollo por filas
La fórmula para el desarrollo por la fila \(i\) de la matriz \(A\) es
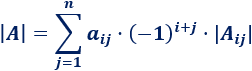
siendo \(a_{ij}\) los elementos de la fila \(i\) y \(A_{ij}\) la que se obtiene al eliminar la fila \(i\) y la columna \(j\) a la matriz \(A\).
Consejo: escoged siempre la fila o la columna que más 0's tenga (en caso de haberlos), para evitar tantas operaciones.
Desarrollo por columnas
El desarrollo por columnas es análogo. La fórmula para el desarrollo por la columna \(j\) es
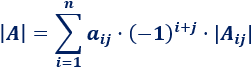
Más ejemplos en cálculo de determinantes.
Calculadoras de matrices:
- Calculadora para multiplicar matrices
- Calculadora de determinantes
- Calculadora de la matriz inversa
- Calculadora de la regla de Cramer
Más información y problemas resueltos de álgebra matricial: