Ecuaciones matriciales
En esta página vamos a explicar cómo resolver ecuaciones matriciales. En total, resolveremos 7 ecuaciones. La mayoría de las matrices son cuadradas y de dimensión 2 ó 3.
Introducción
Una ecuación matricial es una ecuación cuya incógnita es una matriz. Para poder resolver una ecuación matricial, tendremos que sumar, restar y multiplicar matrices y calcular matrices inversas.
Un ejemplo de una ecuación matricial es
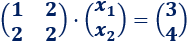
La incógnita de la ecuación es la matriz

Y la solución de la ecuación es
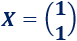
Si os fijáis, podemos calcular el producto de la ecuación matricial obteniendo así un sistema de ecuaciones lineales:
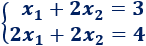
Pero, generalmente, no resolveremos la ecuación matricial resolviendo el sistema de ecuaciones lineales asociado (frecuentemente tendríamos 9 ó más ecuaciones), sino multiplicando por las matrices inversas que aparecen en la ecuación.
Por ejemplo, si definimos las matrices
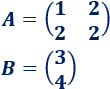
Entonces, la ecuación matricial que tenemos es

La matriz \(A\) es regular (determinante distinto de 0) y, por tanto, tiene matriz inversa:
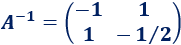
Multiplicamos toda la ecuación por la inversa de \(A\) (la matriz \(I\) es la identidad):
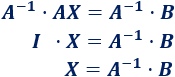
Por tanto, podemos resolver la ecuación calculando el producto de la matriz inversa de \(A\) por la matriz \(B\):
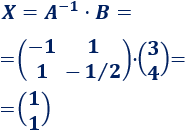
Sin embargo, no siempre es todo tan fácil. Por ejemplo, si las matrices de la ecuación no son cuadradas, no podemos calcular su inversa. Entonces, tendremos que averiguar cómo resolverla.
Ecuaciones matriciales resueltas
Ecuación matricial 1

donde \(A\), \(B\) y \(C\) son las matrices
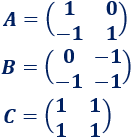
Solución:
Pasamos la matriz \(B\) restando al otro lado:
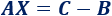
La matriz \(A\) tiene inversa y es
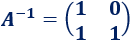
Multiplicamos la ecuación por la inversa de \(A\) para calcular la matriz solución de la ecuación:
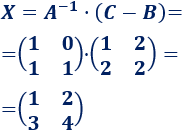
Ecuación matricial 2
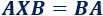
donde \(A\) y \(B\) son las matrices
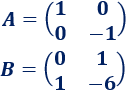
Solución:
Las matrices \(A\) y \(B\) tienen inversa y son
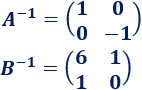
Multiplicamos la ecuación por la inversa de \(A\):
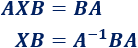
Y por la inversa de \(B\):
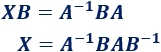
Calculamos los productos matriciales:
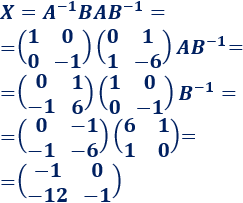
Ecuación matricial 3
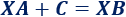
donde \(A\), \(B\) y \(C\) son las matrices
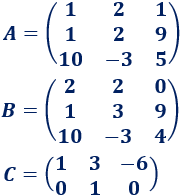
Solución:
Pasamos el sumando \(XB\) restando al otro lado:
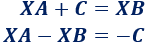
Extraemos factor común de la matriz \(X\) en el lado izquierdo:
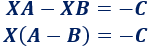
Por tanto, si la matriz \(A-B\) es regular, multiplicamos por su inversa para hallar la solución de la ecuación:
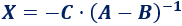
La resta de las matrices \(A\) y \(B\) es

La matriz tiene inversa y es
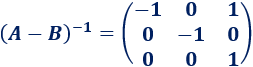
Observad que la matriz es igual a su inversa.
Calculamos la incógnita:
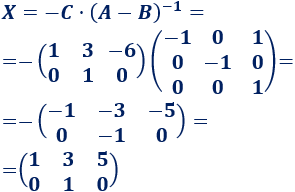
Ecuación matricial 4
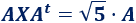
donde \(A\) es la matriz
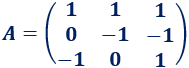
Solución:
La matriz \(A\) tiene inversa y es
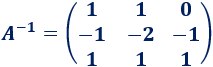
Recordad que la matriz inversa de la traspuesta de una matriz \(A\) es la traspuesta de la inversa de \(A\):
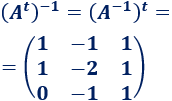
Multiplicamos la ecuación por las inversas:
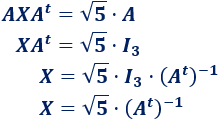
Por tanto, la solución de la ecuación matricial es
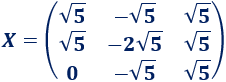
Ecuación matricial 5

donde \(A\) y \(B\) son las matrices
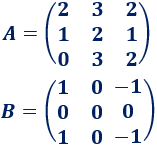
Solución:
Sacamos factor común de la matriz \(X\) en la ecuación:
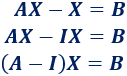
siendo \(I\) la matriz identidad.
Si la matriz \(A-I\) es regular, entonces la solución de la ecuación es
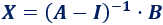
Calculamos la resta de las matrices \(A\) e \(I\):
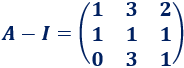
La matriz tiene inversa y es
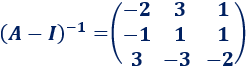
Calculamos la matriz incógnita:
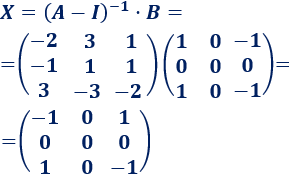
Ecuación matricial 6

donde \(A\), \(B\) y \(C\) son las matrices
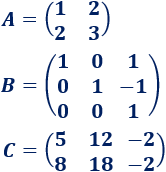
Solución:
Como las matrices \(A\) y \(B\) tienen inversa, sólo tenemos que multiplicar la ecuación por ellas:
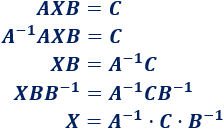
Calculamos las inversas:
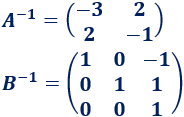
Calculamos la matriz incógnita:
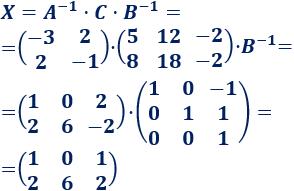
Podéis encontrar más problemas de este tipo en ecuaciones matriciales y sistemas.
Calculadoras de matrices:
- Calculadora para multiplicar matrices
- Calculadora de determinantes
- Calculadora de la matriz inversa
- Calculadora de la regla de Cramer
Más información y problemas resueltos de álgebra matricial:
- Suma de matrices
- Producto de matrices
- Determinantes de matrices
- Matriz inversa
- Regla de Cramer
- Eliminación de Gauss
- Otros temas de álgebra matricial