Multiplicación de matrices
En esta página vamos a explicar cómo se multiplican las matrices. Para que resulte más sencillo, primero vamos a empezar por el producto de una matriz fila por una matriz columna.
Índice de contenidos:
- 5 primeros ejemplos
- Propiedades del producto
- 5 ejemplos más de productos
Enlaces:
Producto matricial 1
Empezamos por el siguiente producto de matrices (fila por columna):
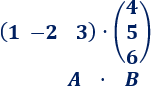
La fila de la matriz \(A\) tiene 3 elementos (3 columnas) y la columna de la matriz \(B\) también tiene 3 elementos (3 filas).
El resultado de la multiplicación \(A·B\) es la suma del primer elemento de \(A\) por el primero de \(B\) más el segundo elemento de \(A\) por el segundo de \(B\) más el tercer elemento de \(A\) por el tercero de \(B\):

Nota: es necesario escribir el resultado entre paréntesis porque es una matriz de dimensión 1x1, no un escalar.
Observad que el número de columnas de \(A\) tiene que coincidir con el número de filas de \(B\).
Hemos elegido estas dimensiones porque los productos matriciales siempre se calculan multiplicando las filas de \(A\) por las columnas de \(B\).
Producto matricial 2
Ahora vamos a multiplicar una matriz de dos filas por una matriz columna:
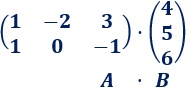
El resultado del producto es una matriz columna con dos filas. En la primera fila tenemos el resultado de la primera fila de \(A\) por la columna de \(B\) y, en la segunda, la segunda fila de \(A\) por la columna de \(B\):
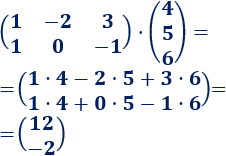
Producto matricial 3
Ahora vamos a multiplicar una matriz con una fila por una matriz con dos columnas:
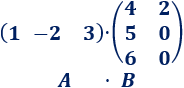
El resultado del producto es una matriz fila con dos columnas. En la primera columna tenemos el resultado de la fila de \(A\) por la primera columna de \(B\) y, en la segunda, la fila de \(A\) por la segunda columna de \(B\):
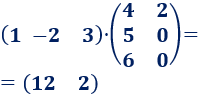
Generalización
Si \(A\) es una matriz de dimensión \(mxn\) y \(B\) es de dimensión \(nxr\), entonces el producto \(A·B\) es una matriz de dimensión \(mxr\).
¡Importante! El número de filas de \(B\) tiene que ser igual al número de columnas de \(A\).
La matriz \(A·B\) tiene en la fila \(i\) y columna \(j\) el resultado de multiplicar la fila \(i\) de \(A\) por la columna \(j\) de \(B\).
Producto matricial 4
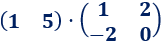
Las dimensiones de las matrices son 1x2 y 2x2. El resultado es una matriz 1x2.
Multiplicamos las matrices:
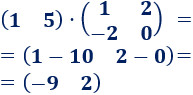
Producto matricial 5
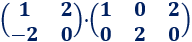
Las dimensiones de las matrices son 2x2 y 2x3. El resultado es una matriz 2x3.
Multiplicamos las matrices:
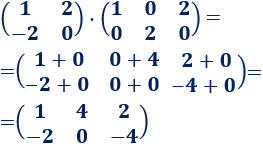
Hacemos un inciso para numerar algunas de las propiedades más importantes del producto de matrices.
Propiedades del producto de matrices
-
El producto de matrices no es conmutativo. Es decir, el producto de matrices \(A·B\) suele ser distinto del producto \(B·A\).
De hecho, si las matrices \(A\) y \(B\) no son cuadradas, alguno de los dos productos no se puede calcular.
-
La matriz identidad \(I\) (de dimensión adecuada) es el neutro del producto matricial. Es decir, para toda matriz \(A\), \(I·A = A\) y \(A·I=A\).
-
Si el producto de dos matrices es \(0\), no significa que necesariamente una de las dos matrices sea la matriz nula (matriz de ceros).
-
Para algunas matrices cuadradas, \(A\), existe una matriz llamada inversa, \(A^{-1}\), tal que los productos \(A·A^{-1}\) y \(A^{-1}·A\) son iguales a la matriz identidad.
-
El producto de matrices diagonales es diagonal y el producto de matrices triangulares es triangular.
Producto matricial 6
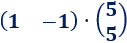
Las dimensiones de las matrices son 1x2 y 2x1. El resultado es una matriz 1x1.
Multiplicamos las matrices:
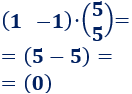
Producto matricial 7
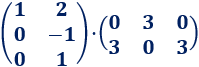
Las dimensiones de las matrices son 3x2 y 2x3. El resultado es una matriz 3x3.
Multiplicamos las matrices:
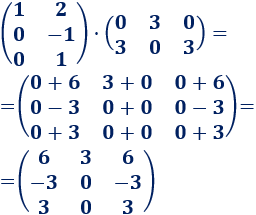
Producto matricial 8
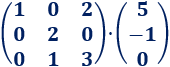
Las dimensiones de las matrices son 3x3 y 3x1. El resultado es una matriz 3x1.
Multiplicamos las matrices:
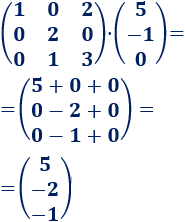
Producto matricial 9
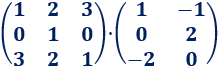
Las dimensiones de las matrices son 3x3 y 3x2. El resultado es una matriz 3x2.
Multiplicamos las matrices:
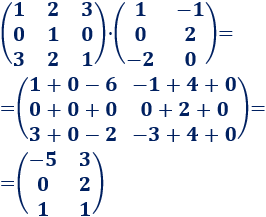
Producto matricial 10
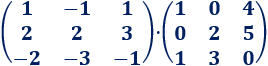
Las dimensiones de las matrices son 3x3 y 3x3. El resultado es una matriz 3x3.
Multiplicamos las matrices:
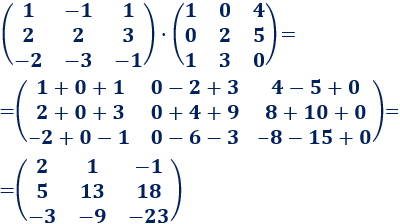
Podéis encontrar más problemas de este tipo en producto de matrices.
Calculadoras de matrices:
- Calculadora para multiplicar matrices
- Calculadora de determinantes
- Calculadora de la matriz inversa
- Calculadora de la regla de Cramer
Más información y problemas resueltos de álgebra matricial: