Regla de Cramer: ejemplos
En esta página explicamos la regla de Cramer y la aplicamos para resolver 4 sistemas de ecuaciones lineales (dos sistemas de dimensión 2x2 y dos sistemas de dimensión 3x3).
Enlace: Calculadora de la regla de Cramer.
Introducción
La regla de Cramer proporciona la solución de sistemas de ecuaciones lineales compatibles determinados (con una única solución) mediante el cálculo de determinantes. Se trata de un método muy rápido para resolver sistemas, sobre todo, para sistemas de dimensión 2x2 y 3x3. Para dimensiones mayores, los determinantes son bastante más engorrosos.
Recordad que un sistema de ecuaciones puede escribirse en forma matricial como
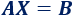
donde
-
\(A\) es la matriz de coeficientes del sistema,
-
\(X\) es la matriz con las incógnitas,
-
\(B\) es la matriz con los términos independientes de las ecuaciones.
Para poder aplicar Cramer, la matriz \(A\) tiene que ser cuadrada y regular (determinante distinto de 0).
La regla de Cramer establece que la incógnita \(x_k\) de la solución del sistema, cuyos coeficientes están en la columna \(k\) de \(A\), es
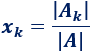
donde\(A_k\) es como la matriz \(A\) pero cambiando su columna número \(k\) por la columna de términos independientes, \(B\).
Ejemplos de la regla de Cramer
Ejemplo 1
Sistema de dimensión 2x2:
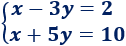
Solución:
La matriz de coeficientes del sistema es
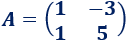
La matriz de incógnitas es
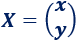
La matriz de términos independientes es
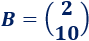
Calculamos el determinante de \(A\):
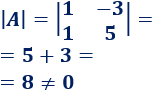
Podemos aplicar la regla de Cramer.
La primera incógnita es \(x\), cuyos coeficientes son los de la primera columna de \(A\). La matriz \(A_1\) es como \(A\) pero cambiando dicha columna por la columna \(B\):
Calculamos \(x\):
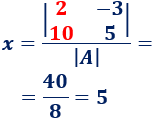
La segunda incógnita es \(y\) y sus coeficientes son los de la segunda columna de \(A\). Tenemos que calcular el determinante de la matriz
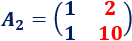
Calculamos \(y\):
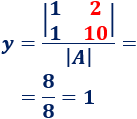
Por tanto, la solución del sistema es
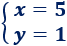
Ejemplo 2
Sistema de dimensión 2x2:
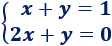
Solución:
La matriz de coeficientes del sistema es
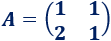
La matriz de términos independientes es
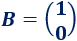
Calculamos el determinante de \(A\):
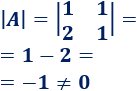
Podemos aplicar la regla de Cramer.
La matriz \(A_1\) es
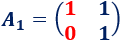
Calculamos \(x\):
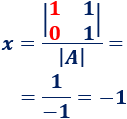
La matriz \(A_2\) es
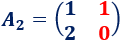
Calculamos \(y\):
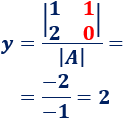
Por tanto, la solución del sistema es
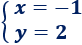
Ejemplo 3
Sistema de dimensión 3x3:
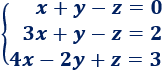
Solución:
La matriz de coeficientes del sistema es
La matriz de incógnitas es
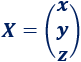
La matriz de términos independientes es
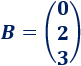
Calculamos el determinante de \(A\):
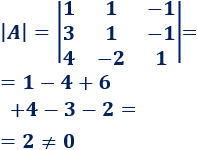
Podemos aplicar la regla de Cramer.
La matriz \(A_1\) es como \(A\) pero cambiando la columna 1 por la columna \(B\):
Calculamos \(x\):
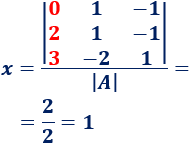
La matriz \(A_2\) es como \(A\) pero cambiando la columna 2 por la columna \(B\):
Calculamos \(y\):
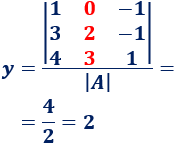
La matriz \(A_3\) es como \(A\) pero cambiando la columna 3 por la columna \(B\):
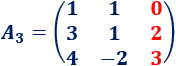
Calculamos \(z\):
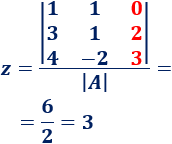
Por tanto, la solución del sistema es
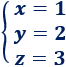
Ejemplo 4
Sistema de dimensión 3x3:
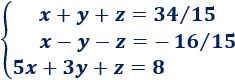
Solución:
La matriz de coeficientes del sistema es
La matriz de términos independientes es
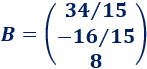
Calculamos el determinante de \(A\):
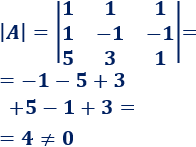
Podemos aplicar la regla de Cramer.
La matriz \(A_1\) es
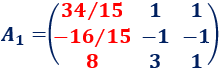
Calculamos \(x\):
La matriz \(A_2\) es
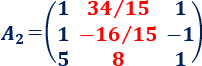
Calculamos \(y\):
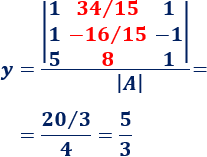
La matriz \(A_3\) es
Calculamos \(z\):
Por tanto, la solución del sistema es
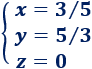
Podéis encontrar más problemas de este tipo en la Regla de Cramer.
Calculadoras de matrices:
- Calculadora para multiplicar matrices
- Calculadora de determinantes
- Calculadora de la matriz inversa
- Calculadora de la regla de Cramer
Más información y problemas resueltos de álgebra matricial: