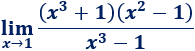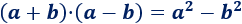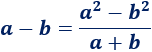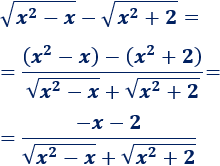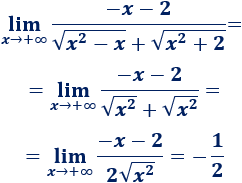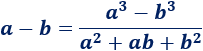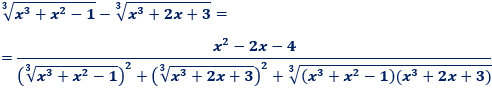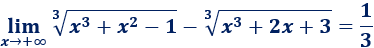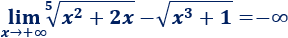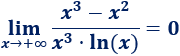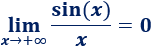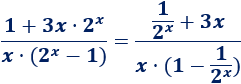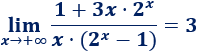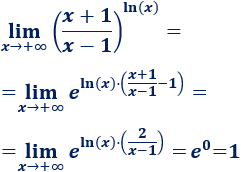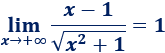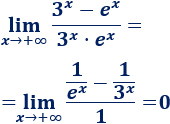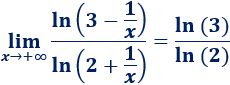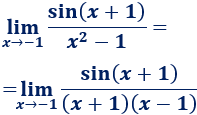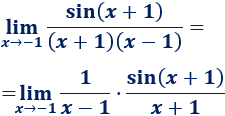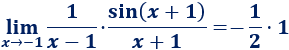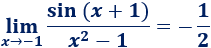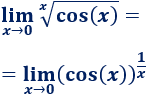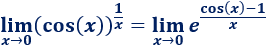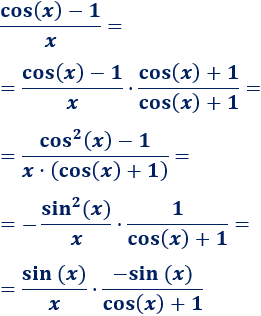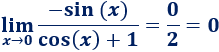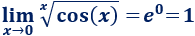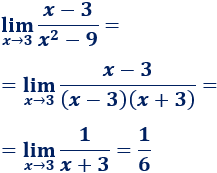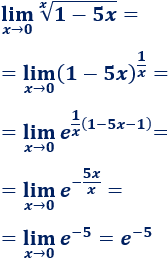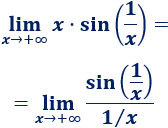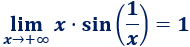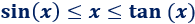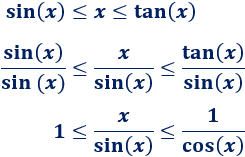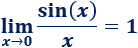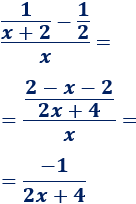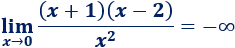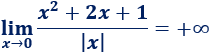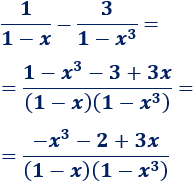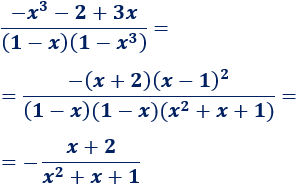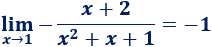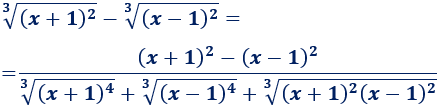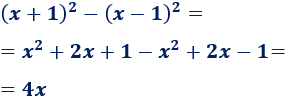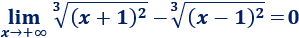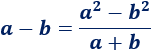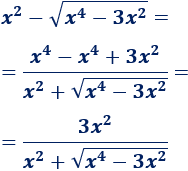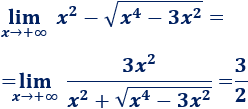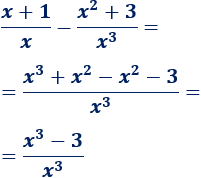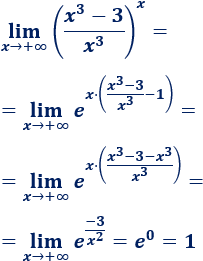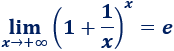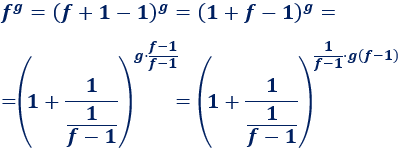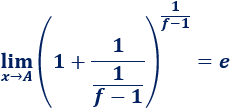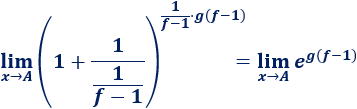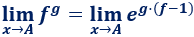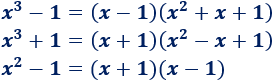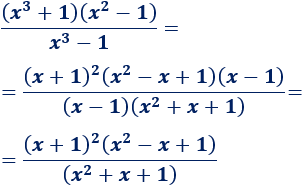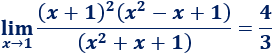Cálculo de límites
Más de 50 límites resueltos y explicados
En esta página calculamos límites de funciones de una variable. Primero, hacemos una pequeña introducción y recordamos los conceptos de límite, límites laterales e indeterminaciones. Después, proporcionamos algunas reglas y procedimientos útiles para calcular límites y evitar las indeterminaciones.
En total, resolvemos detalladamente más de 50 límites, sin utilizar la regla de L'Hôpital ni infinitésimos.
Índice:
- Introducción
- Concepto de límite
- Definición formal
- Límites laterales
- Límites infinitos
- Reglas básicas
- Primeros límites resueltos (básicos)
- Indeterminaciones
- Procedimientos o técnicas
- Más límites resueltos
Más límites resueltos: 50 límites resueltos, Indeterminación 0/0, Indeterminación ∞/∞, Indeterminación 0·∞, Indeterminación 1∞.
1. Introducción
Las funciones matemáticas se utilizan en otros ámbitos, por ejemplo, para calcular los beneficios o los costes de una empresa, la velocidad o aceleración de un móvil, etc., por lo que es importante conocer el comportamiento de una función.
Por ejemplo, la siguiente función no está definida en \(x=0\) ni en \(x = -1\) (porque no se puede dividir entre \(0\)):
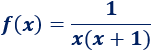
Sin embargo, sí podemos preguntarnos cómo se comporta la función cuando \(x\) se aproxima a \(0\) o cuando se aproxima a \(-1\). ¿Y si \(x\) crece o decrece indefinidamente? Los límites de la función \(f\) nos proporcionan las respuestas.
Además de ayudarnos a visualizar la gráfica de la función, los límites también se utilizan para estudiar otras propiedades, como la continuidad de una función, la diferenciabilidad, etc.
2. Concepto de límite
Dada una función \(f: \mathbb{R} \rightarrow \mathbb{R}\) y un punto \(x_0 \in \mathbb{R}\), el límite de \(f\) cuando \(x\) tiende a \(x_0\) se representa como
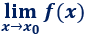
En un principio, este límite es el valor que toma \(f\) en el punto \(x_0\), es decir, \(f(x_0)\). Si \(f(x_0)\) no existe (por ejemplo, cuando \(x_0\) anula el denominador de \(f\)), entonces el límite es el valor al que \(f\) se aproxima cuando \(x\) se aproxima a \(x_0\).
Por ejemplo, sea la función
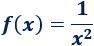
No existe \(f(0)\), pero cuanto más se aproxima \(x\) a \(0\), la función crece más y más, como podemos observar en la gráfica:
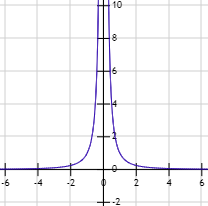
Por tanto, el límite de \(f\) cuando \(x\) tiende a \(0\) es infinito:
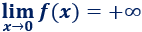
También, podemos predecir el comportamiento de la función cuando \(x\) crece o decrece indefinidamente (cuando \(x\) tiende a \(\pm \infty\)). Cuando esto ocurre, la función \(f(x) =1/x^2\) se aproxima cada vez más a \(0\):
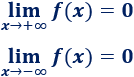
3. Definición formal
Para los interesados, la definición formal del límite es la siguiente:
Sea la función \(f: \mathbb{R} \rightarrow \mathbb{R}\) y sea \(x_0 \in \mathbb{R}\), existe el límite de \(f\) cuando \(x\) tiende a \(x_0\) y es \(K \in \mathbb{R}\) si \(\forall \varepsilon > 0\), \(\exists \delta > 0\) tal que
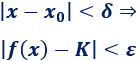
Matemáticamente, lo resumimos con la notación de límite:
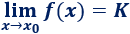
La definición del límite cuando \(x\to \infty\) es ligeramente distinta.
4. Límites laterales
Vimos en un ejemplo anterior que la función \(f(x) = 1/x^2\) tiende a \(+\infty\) cuando \(x\) tiende a \(0\). Sin embargo, no ocurre los mismo con la función \(f(x) = 1/x\):
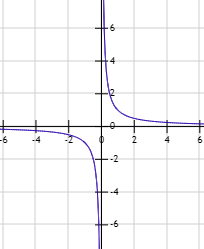
En este caso, la función crece indefinidamente cuando \(x\) se aproxima a \(0\) por la derecha (de \(0\)) y decrece indefinidamente cuando se aproxima a \(0\) por la izquierda.
En este caso, decimos que no existe el límite \(x\to 0\), pero sí existen los límites laterales.
El límite lateral de \(f\) por la derecha de \(0\) es
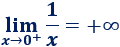
Y el límite lateral de \(f\) por la izquierda de \(0\) es
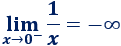
El límite de \(f(x)\) cuando \(x\) tiende a \(x_0\) existe si y sólo si existen los límites laterales y, además, coinciden:
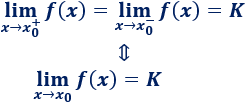
5. Límites infinitos
Hemos estado hablando, básicamente, de límites en puntos finitos \(x_0\in\mathbb{R}\), pero también podemos preguntarnos cuál es límite de una función cuando \(x\) crece o decrece indefinidamente, es decir, cuando \(x\to +\infty\) y cuando \(x\to -\infty\).
Por ejemplo, la siguiente función tiende a \(2\) cuando \(x\) tiende a \(\pm \infty\):
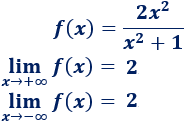
Más adelante, veremos cómo se calculan estos límites.
La gráfica de la función anterior es
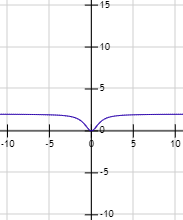
Obviamente, no podemos hablar de límites laterales cuando \(x\) tiende a infinito.
6. Reglas básicas
Hasta el momento, no hemos explicado cómo calcular los límites.
-
Lo primero que hacemos para calcular el límite de \(f\) en el punto \(x_0\) es comprobar si se puede calcular \(f(x_0)\) porque, en este caso, el límite es dicho valor:
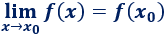
Es decir, en este caso sólo hay que cambiar las \(x\) por \(x_0\).
Por ejemplo,
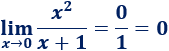
Nota: en una función definida a trozos, hay que calcular primero los límites laterales en \(x_0\) si es un punto de cambio de definición.
-
Es importante comprobar que la función está escrita en su mínima expresión.
Por ejemplo, el siguiente límite parece indeterminado porque no se puede dividir \(0\) entre \(0\):
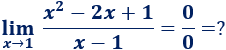
Sin embargo, podemos simplificar la función:
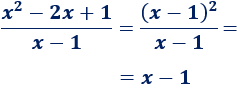
De este modo, el límite es muy fácil de calcular:
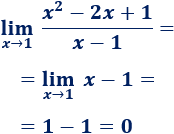
Ahora vamos a ver las reglas que nos permiten calcular los límites cuando sustituimos \(x\) por \(x_0\). Escribiremos el signo de interrogación "?" para las indeterminaciones, de las cuales hablaremos más adelante.
Sea \(K\) un número real distinto de \(0\).
Sumar o restar infinito:

La resta de infinitos de signo distinto es indeterminada: \(\infty -\infty = ?\).
Nota: para ver que estas reglas tienen su lógica, consideremos los siguientes casos:
- Un número muy muy grande más un número muy muy grande es un número muy muy grande, de donde deducimos la regla \(+\infty + \infty = +\infty\).
- Un número muy muy grande más un número finito \(K\) sigue siendo un número muy muy grande: \(+\infty + K = +\infty\). Por ejemplo, podemos pensar que agregar o eliminar un grano de arena de una playa no afecta demasiado al número total de granos.
- Un número muy muy grande menos un número finito \(K\) sigue siendo un número muy muy grande: \(+\infty - K = +\infty\).
Multiplicar por infinito:
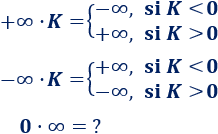
El producto \(0·\infty\) es una indeterminación.
El producto de infinitos es infinito. El signo del resultado se obtiene por la regla de los signos:
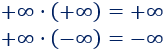
Dividir entre cero:
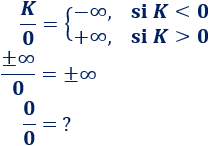
El cociente \(0/0\) es una indeterminación.
Dividir entre infinito:
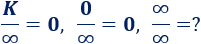
El cociente \(\infty/\infty\) es una indeterminación.
Elevar a \(0\):
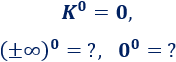
Las potencias \(\infty^0\) y \(0^0\) son indeterminaciones.
Elevar a infinito:
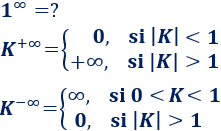
La potencia \(1^\infty\) es una indeterminación.
Nota: \(0^\infty =0\) y \(\infty^\infty = \infty\) no son indeterminaciones.
7. Primeros límites resueltos (básicos)
A continuación, resolvemos 5 límites con \(x\to a\in\mathbb{R}\) (\(a\) es un número finito).
Límite 1
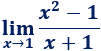
Solución:
Al sustituir \(x\) por 1, obtenemos el resultado 0/2, así que el límite es 0:
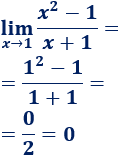
Límite 2
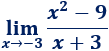
Solución:
Si sustituimos \(x\) por \(-3\) obtenemos una indeterminación:
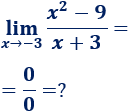
Sin embargo, podemos simplificar la función antes de calcular el límite:
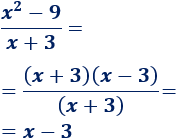
Calculamos el límite (sustituyendo):
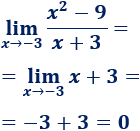
Límite 3
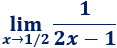
Solución:
Sustituimos \(x\) por \(1/2\):
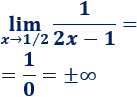
Hemos escrito el signo \(\pm\) porque el signo del límite depende del lado por el que nos aproximamos a \(1/2\).
Si nos aproximamos por la derecha, el denominador es positivo y se aproxima a 0, así que el límite es \(+\infty\); por el otro lado, el límite es \(-\infty\):
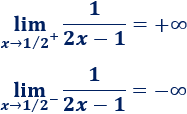
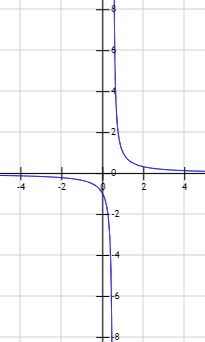
Gráfica de la función:
Límite 4
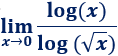
Solución:
No podemos sustituir \(x=0\) porque no está definido el logaritmo de 0. Aplicando las propiedades de los logaritmos,
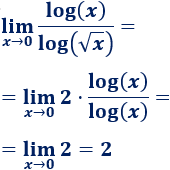
Límite 5
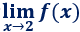
siendo \(f\) la siguiente función definida por partes:
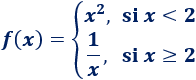
Solución:
Como tenemos que calcular el límite en el punto donde cambia la definición de la función, tenemos que calcular los límites laterales y ver si coinciden.
Límite por la izquierda:
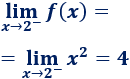
Límite por la derecha:
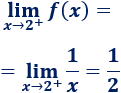
Como los límites laterales no coinciden, no existe el límite en el punto \(x=2\):
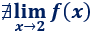
Gráfica de la función:
8. Indeterminaciones
Las indeterminaciones son las 7 operaciones algebraicas siguientes cuyo resultado no podemos predecir:
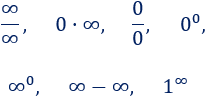
Por ejemplo, en los dos siguientes límites aparece la indeterminación cociente de infinitos:
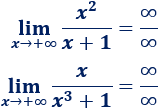
El resultado del primer límites es \(+\infty\) y el del segundo es \(0\).
En el siguiente apartado vemos algunos procedimientos para resolver las indeterminaciones.
9. Procedimientos o técnicas
La mayoría de los procedimientos los utilizamos cuando \(x\to\infty\).
Cociente de polinomios:
En el límite de un cociente de polinomios \(P(x)/Q(x)\) suele aparecer un cociente de infinitos (\(\infty/\infty\)). Escribimos \(\delta P\) y \(\delta Q\) para referirnos al grado del polinomio \(P\) y \(Q\), respectivamente:
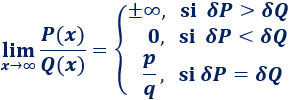
En el primer caso, el signo del infinito depende de los grados de los polinomios y de sus coeficientes.
En el tercer caso, \(p\) es el coeficiente director de \(P(x)\) y \(q\) es el de \(Q(x)\).
Problema 1
Calcular los siguientes límites:
-
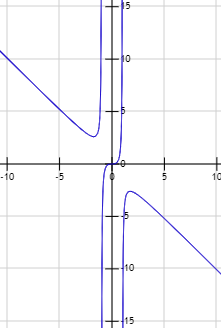
\(\lim_{x\to +\infty} \frac{x^3}{x^2+1}\)
-
\(\lim_{x\to -\infty} \frac{x^3}{x^2+1}\)
-
\(\lim_{x\to -\infty} \frac{-x^3}{x^2+1}\)
-
\(\lim_{x\to +\infty} \frac{x^3}{1-x^2}\)
Resolvemos:
En estos límites tenemos que aplicar el criterio de los polinomios. Más exactamente, todos presentan la indeterminación cociente de infinitos y en todos ellos, el grado del numerador es mayor que el del denominador. Por tanto, el resultado de todos los límites es infinito, pero debemos calcular el signo del infinito.
-
\(\lim_{x\to +\infty} \frac{x^3}{x^2+1}\)
Los coeficientes son positivos y el infinito es positivo, por tanto, el límite es positivo:
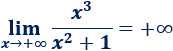
-
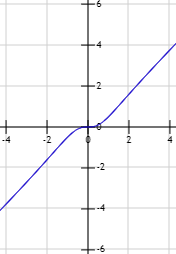
\(\lim_{x\to -\infty} \frac{x^3}{x^2+1}\)
Los coeficientes son positivos y el infinito es negativo. Como el grado del numerador es impar y el del numerador es par, el resultado es negativo (negativo entre positivo):
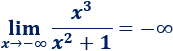
Gráfica de la función:
-
\(\lim_{x\to -\infty} \frac{-x^3}{x^2+1}\)
El infinito es negativo. Al cuadrado es positivo. Al cubo es negativo, pero tiene el coeficiente negativo. Por tanto, tenemos positivo entre positivo:
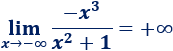
-
\(\lim_{x\to +\infty} \frac{x^3}{1-x^2}\)
Positivo entre negativo, así que el resultado es negativo:
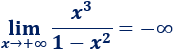
Gráfica de la función:
Cociente de exponenciales:
Normalmente, para resolver límites con exponenciales, dividimos la función entre alguna de las exponenciales (generalmente, la que tiene base mayor para conseguir bases menores que 1).
Problema 2
Calcular los siguientes límites:
-
\(\lim_{x\to -\infty} \frac{3^x}{2^x-5}\)
-
\(\lim_{x\to -\infty} 3^x·x -2^x\)
-
\(\lim_{x\to +\infty} \frac{ln(3^x)}{x-2}\)
-
\(\lim_{x\to +\infty} \frac{ln(5^x+3^x+2^x)}{ln(5^x+2^x)}\)
Resolvemos:
-
\(\lim_{x\to -\infty} \frac{3^x}{2^x-5}\)
Como las bases son mayores que \(1\), tenemos una indeterminación:
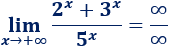
Dividimos la función entre la potencia \(5^x\):
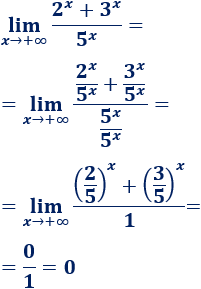
Las potencias del numerador tienden a \(0\) (porque \(2/5\) y \(3/5\) son menores que \(1\)).
-
\(\lim_{x\to -\infty} 3^x·x -2^x\)
Tenemos una resta de infinitos:
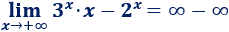
Dividimos entre \(3^x\):
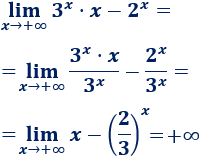
-
\(\lim_{x\to +\infty} \frac{ln(3^x)}{x-2}\)
Aplicamos las propiedades de los logaritmos y obtenemos un cociente de polinomios con el mismo grado, así que el resultado es el cociente de los coeficientes principales:
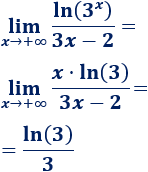
-
\(\lim_{x\to +\infty} \frac{ln(5^x+3^x+2^x)}{ln(5^x+2^x)}\)
Tenemos la indeterminación \(\infty / \infty\).
Extraemos factor común de la potencia \(5^x\) en los argumentos de los logaritmos y aplicamos las propiedades de los logaritmos:
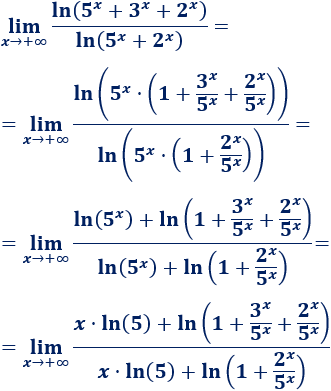
Observad que el límite del logaritmo de la derecha del numerador y del denominador tienden a \(0\) (porque tienden al logaritmo de \(1\)).
Por tanto, el límite anterior coincide con el siguiente límite:
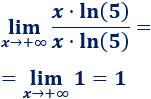
Indeterminación \(1^\infty \):
Esta indeterminación aparece, normalmente, en los límites con la forma
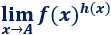
donde la función \(f(x)\) tiende a 1 y \(h(x)\) tiende a infinito. El punto \(A\) del límite puede ser un punto finito o \(\pm \infty\).
En este caso, aplicamos la siguiente fórmula:
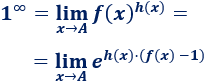
Problema 3
Calcular los siguientes límites:
-
\(\lim_{x\to +\infty} \left( \frac{1+x}{x-1} \right) ^{x}\)
-
\(\lim_{x\to +\infty} \left( 1+\frac{1}{x} \right) ^{x}\)
-
\(\lim_{x\to +\infty} \left( 1+\frac{1}{x^3} \right) ^{x^2}\)
-
\(\lim_{x\to +\infty} \left( 1+\frac{x}{1+2x^2} \right)^{x}\)
Resolvemos:
-
\(\lim_{x\to +\infty} \left( \frac{1+x}{x-1} \right) ^{x}\)
La fracción tiende a 1 (cociente de polinomios con el mismo grado con coeficientes \(1\)), así que tenemos la indeterminación \(1^\infty\). Aplicamos la fórmula:
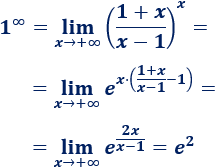
-
\(\lim_{x\to +\infty} \left( 1+\frac{1}{x} \right) ^{x}\)
Aplicamos la fórmula:
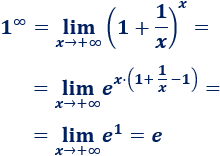
-
\(\lim_{x\to +\infty} \left( 1+\frac{1}{x^3} \right) ^{x^2}\)
Aplicamos la fórmula:
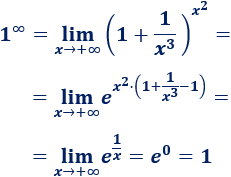
-
\(\lim_{x\to +\infty} \left( 1+\frac{x}{1+2x^2} \right) ^{x}\)
Aplicamos la fórmula:
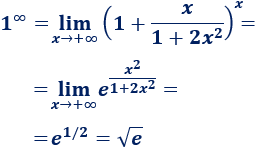
Cociente de raíces:
Cuando la función está formada por un cociente en el que aparecen raíces, el límite depende del orden de las raíces, al igual que en los cocientes de polinomios.
Suelen aparecer las indeterminaciones resta de infinitos y cociente de infinitos. Normalmente, es suficiente multiplicar y dividir por el conjugado y/o comparar los órdenes de las raíces y grados de las \(x\).
Fórmulas que pueden ayudar (para resta de infinitos):
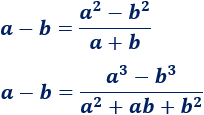
Por ejemplo,
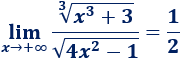
El grado del numerador es 1 porque tenemos la raíz cúbica de un polinomio de grado 3. El del denominador es 1 porque tenemos la raíz cuadrada de un cuadrado. Por tanto, el límite es el cociente de los coeficientes principales:
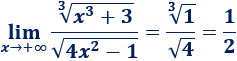
Gráfica de la función:
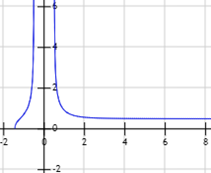
Problema 4
Calcular los siguientes límites:
-
\(\lim_{x\to +\infty} \frac{3x}{\sqrt{x+3x^2}} \)
-
\(\lim_{x\to +\infty} \frac{\sqrt[3]{2x-1} - \sqrt{2x^2+1}}{\sqrt[3]{5x^3-2}} \)
-
\(\lim_{x\to +\infty} \sqrt{x^2+x-1} - \sqrt{x^2-2x} \)
-
\(\lim_{x\to +\infty} \frac{\sqrt{3x^2-2x}-\sqrt{3x^3+5x^2}}{\sqrt{5x}} \)
Resolvemos:
-
\(\lim_{x\to +\infty} \frac{3x}{\sqrt{x+3x^2}} \)
El grado del numerador es 1 y el coeficiente director es 3.
El grado del denominador es la raíz cuadrada de un cuadrado (es decir, 1) y su coeficiente director es raíz de 3. Por tanto,
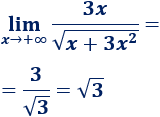
-
\(\lim_{x\to +\infty} \frac{\sqrt[3]{2x-1} - \sqrt{2x^2+1}}{\sqrt[3]{5x^3-2}} \)
El grado de la raíz de la derecha del numerador es \(2/2 = 1\) y el de la izquierda es \(1/3\). Por tanto, el grado del numerador es 1 y el coeficiente director es \(\sqrt{2}\).
El grado del denominador es \(3/3=1\) y su coeficiente es \(\sqrt[3]{5}\).
Calculamos el límite:
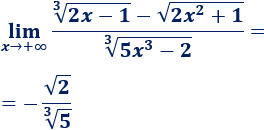
-
\(\lim_{x\to +\infty} \sqrt{x^2+x-1} - \sqrt{x^2-2x} \)
Como tenemos la indeterminación \(\infty - \infty\), multiplicamos y dividimos por la suma de las raíces. Es decir, si \(a\) y \(b\) son las dos raíces, vamos a realizar las siguientes operaciones:
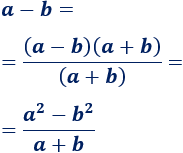
Así, desaparecen las raíces del numerador:
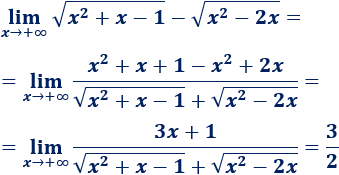
Observad que el grado del numerador y del numerador es 1. En el numerador, el coeficiente director es 3. El coeficiente del denominador es 2 porque tenemos una suma de raíces del mismo orden con coeficientes \(1\): \(\sqrt{1}+\sqrt{1}=2\).
-
\(\lim_{x\to +\infty} \frac{\sqrt{3x^2-2x}-\sqrt{3x^3+5x^2}}{\sqrt{5x}} \)
Calculamos el límite procediendo como en el límite anterior:
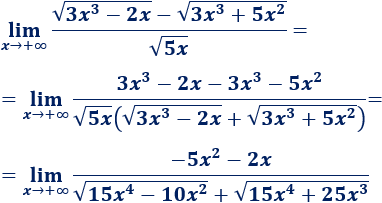
Teniendo en cuenta los grados del numerador y del denominador,
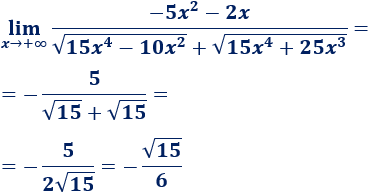
Comparación de funciones:
Muchas veces, es fácil calcular el límite de una función simplemente comparando las funciones que conforman la propia función.
Por ejemplo, el límite cuando \(x\) tiende a \(+\infty\) de la función \(x^5-x^2\) es \(\infty-\infty\). Sin embargo, como \(x^5\) crece más rápido que la función \(x^2\), el límite es \(+\infty\). Dicho de otra forma, el orden del infinito del límite de la primera función es mayor que el de la segunda, así que el resultado es \(\infty\).
Otros ejemplos:
-
un monomio crece más rápido que un logaritmo,
- un monomio crece más rápido que una raíz,
-
una exponencial crece más rápido que un monomio.
Problema 5
Calcular los siguientes límites:
-
\(\lim_{x\to +\infty} \frac{x}{e^x} \)
-
\(\lim_{x\to +\infty} \frac{x-ln(x)}{x} \)
-
\(\lim_{x\to +\infty} x·ln(x)-x·e^x \)
-
\(\lim_{x\to +\infty} \frac{2^x+x^2}{3^x} \)
Resolvemos:
-
\(\lim_{x\to +\infty} \frac{x}{e^x} \)
La exponencial crece mucho más rápido que \(x\), como se puede observar comparando sus gráficas:
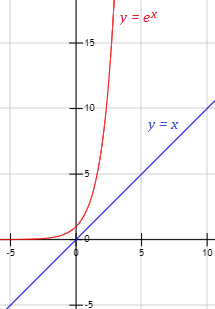
Por tanto,
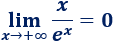
-
\(\lim_{x\to +\infty} \frac{x-ln(x)}{x} \)
El logaritmo crece más lentamente que \(x\):
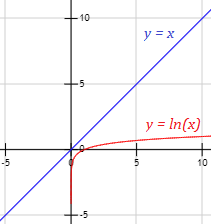
Por tanto, operando un poco,
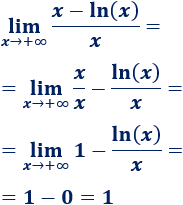
-
\(\lim_{x\to +\infty} x·ln(x)-x·e^x \)
Extrayendo factor común y teniendo en cuenta que la exponencial crece más rápido que el logaritmo,
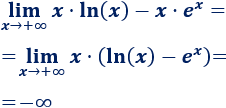
-
\(\lim_{x\to +\infty} \frac{2^x+x^2}{3^x} \)
Descomponemos la fracción en una suma para facilitar la comparación:
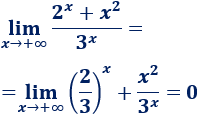
El sumando de la izquierda tiende a \(0\) (porque \(2/3\) es menor que \(1\)) y el de la izquierda tiende a \(0\) (porque la exponencial crece más rápidamente que \(x^2\)).
Aplicación de logaritmos:
Las propiedades de los logaritmos pueden ser útiles para calcular límites, sobre todo, cuando aparecen exponentes. Para ello, utilizamos la propia definición del logaritmo:

De este modo,
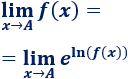
Problema 6
Calcular los siguientes límites:
-
\(\lim_{x\to +\infty} x^{\frac{1}{x}} \)
-
\(\lim_{x\to +\infty} \frac{1}{x}^{\frac{1}{x}} \)
-
\(\lim_{x\to +\infty} \sqrt[3x^2]\frac{e^{x^2}}{x^5} \)
-
\(\lim_{x\to +\infty} \frac{1}{x^2}·x^\frac{1}{x^2+1} \)
Resolvemos:
-
\(\lim_{x\to +\infty} x^{\frac{1}{x}} \)
Tenemos la indeterminación \(\infty ^0\). Aplicamos logaritmos:
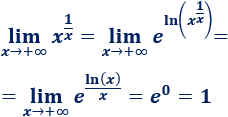
Recordad que \(x\) crece más rápido que el logaritmo de \(x\), así que la fracción del exponente tiende a \(0\).
-
\(\lim_{x\to +\infty} \frac{1}{x}^{\frac{1}{x}} \)
Tenemos la indeterminación \(0^0\). Aplicamos logaritmos:
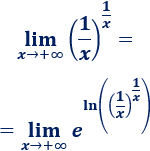
Simplificamos el exponente:
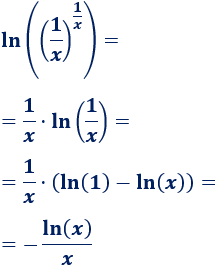
El exponente tiende a \(0\). Por tanto,
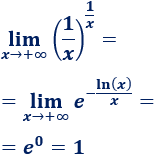
-
\(\lim_{x\to +\infty} \sqrt[3x^2]\frac{e^{x^2}}{x^5} \)
Escribimos la raíz como una potencia:
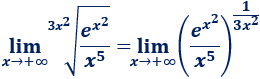
Tenemos la indeterminación \(\infty\) elevado a \(0\). Aplicamos logaritmos:
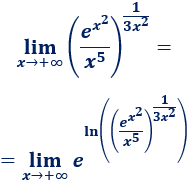
Simplificamos el exponente:
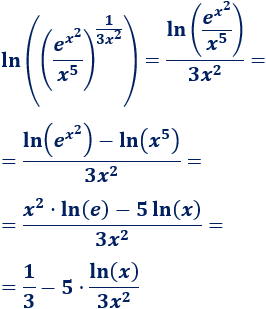
El límite de la fracción es \(0\), así que
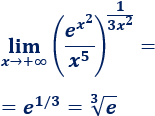
-
\(\lim_{x\to +\infty} \frac{1}{x^2}·x^\frac{1}{x^2+1} \)
Tenemos la indeterminación \(0·\infty ^0\). Aplicamos logaritmos:
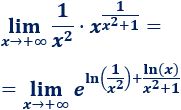
Por un lado,
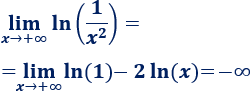
Por otro, como \(x^2\) crece más rápido que el logaritmo,
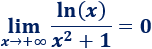
Luego
10. Más límites resueltos
Límite 6
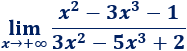
Resolvemos:
Tenemos un cociente de polinomios de igual grado. Su límite es el cociente de sus coeficientes directores:
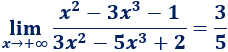
Límite 7
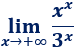
Resolvemos:
Tenemos la indeterminación \(\infty^\infty/\infty\). Reescribimos la función:
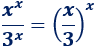
Ahora, tenemos la indeterminación \(\infty^\infty\). Aplicamos logaritmos:
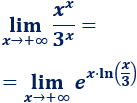
El exponente que tenemos tiende a \(\infty ·\infty\), que es \(\infty\). Por tanto,
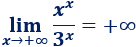
Límite 8
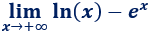
Resolvemos:
Tenemos la indeterminación \(\infty-\infty\).
Como la exponencial crece más rápido que el logaritmo, tiene más influencia en el límite. Por tanto, como su coeficiente es negativo,
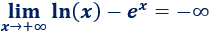
Límite 9
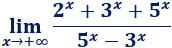
Resolvemos:
Tenemos la indeterminación \(\infty/(\infty -\infty )\).
Dividimos en el numerador y el denominador por la exponencial con mayor base (\(5^x\)):
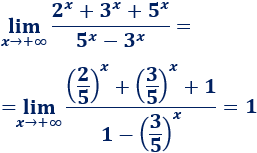
Nota: las exponenciales que quedan tienden a \(0\) porque sus bases son menores que \(1\).
Límite 10
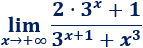
Resolvemos:
Reescribimos el límite:
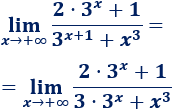
Las exponenciales tienen la misma base y exponente y crecen más rápidamente que \(x^3\). Como hay una exponencial en el numerador y otra en el denominador, el límite es el cociente de sus coeficientes:
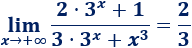
Si es necesario, se puede dividir entre \(3^x\) para ver claramente el resultado:
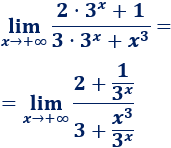
Límite 11
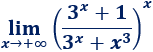
Resolvemos:
Por el límite anterior, sabemos que la base de la exponencial tiende a 1, así que tenemos la indeterminación \(1^\infty\). Aplicamos la fórmula:
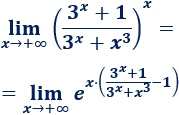
Simplificamos el exponente:
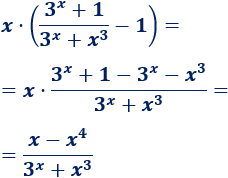
La exponencial tiene más peso que el polinomio, así que el exponente tiende a \(0\). Por tanto,
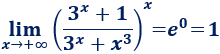
Límite 12
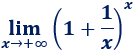
Resolvemos:
Este límite es importante recordarlo. Aplicamos la fórmula para resolver la indeterminación uno elevado a infinito:
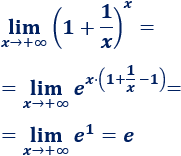
Límite 13
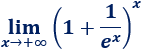
Resolvemos:
Este límite es parecido al anterior. Aplicamos la fórmula para evitar la indeterminación \(1^\infty\):
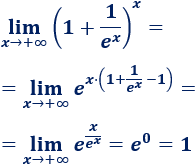
El exponente tiende a \(0\) porque la exponencial crece más rápidamente.
Límite 14
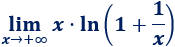
Resolvemos:
Tenemos la indeterminación infinito por cero. Aplicamos las propiedades de los logaritmos:
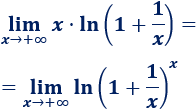
Ya sabemos que el límite del argumento del logaritmo tiende al número \(e\), así que el límite es \(1\):
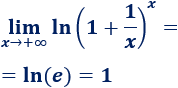
Límite 15
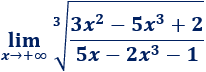
Resolvemos:
Tenemos un cociente de polinomios de igual grado, por tanto,
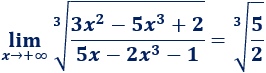
Límite 16
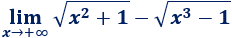
Resolvemos:
Tenemos la indeterminación \(\infty-\infty\).
Para facilitar el cálculo, eliminamos los monomios \(+1\) y \(-1\) que aparecen en las raíces (cuando \(x\) tiende a infinito, son insignificantes):
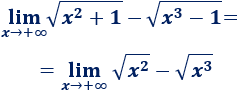
Muy importante: no podemos eliminar los monomios si esto hace que la función se anule, como ocurriría, por ejemplo, con la función \( \sqrt(x^2+1)-\sqrt(x^2-1) \).
Escribimos las raíces como exponentes:
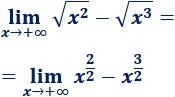
La potencia \(3/2\) es mayor que \(2/2=1\), así que tiene más peso. Luego el límite es menos infinito:
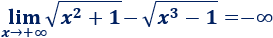
Límite 17
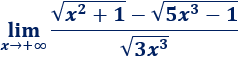
Resolvemos:
Seguimos el mismo razonamiento que en el límite anterior (sin escribir todos los pasos).
En el numerador, el exponente mayor es el de la raíz de la derecha (\(3/2\)). En el denominador, el exponente es \(3/2\). Como coinciden, el límite es el cociente de sus coeficientes:
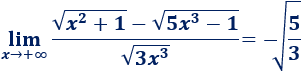
Límite 18
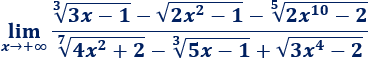
Resolvemos:
Los monomios que tienen más peso en el límite son aquéllos cuyo grado es mayor. Vamos a calcular los grados de las \(x\) del numerador y los de las \(x\) del denominador.
Numerador:
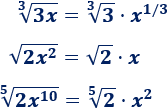
Denominador:
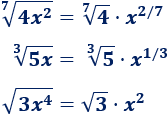
Tanto en el numerador como en el denominador, el grado mayor es \(2\).
En el numerador, se corresponde a la raíz quinta, que está restando. En el denominador, se corresponde a la raíz cuadrada, que está sumando.
Luego, teniendo en cuenta los signos y los coeficientes, el límite es

Límite 19
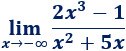
Resolvemos:
Como el grado del polinomio del numerador es mayor, el límite tiende a infinito. Como el límite es cuando \(x\) tiende a \(-\infty\) y el cubo de un negativo es negativo, el resultado también es negativo:
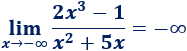
Límite 20
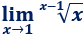
Resolvemos:
Escribimos la raíz como una potencia:
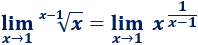
Como tenemos la indeterminación uno elevado a infinito, aplicamos la fórmula:
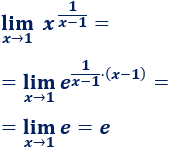
Límite 21
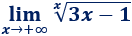
Resolvemos:
Escribimos la raíz como una potencia:
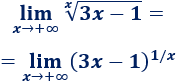
Tenemos la indeterminación infinito elevado a cero. Aplicamos logaritmos:
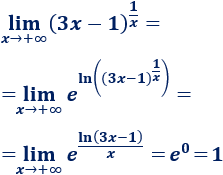
El exponente tiende a \(0\) porque \(x\) crece más rápido que el logaritmo.
Límite 22
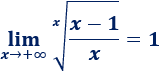
Resolvemos:
Escribimos la raíz como una potencia:
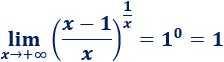
Límite 23 (difícil)
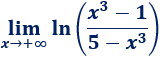
Resolvemos:
Como los polinomios tienen el mismo grado, el límite de su cociente es el cociente de sus coeficientes:
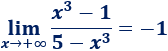
Por tanto, el límite tiende al logaritmo de un número negativo, que no existe. Así que
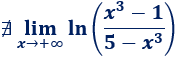
Nota: como curiosidad, podemos resolver el límite si consideramos los números complejos.
Recordad la fórmula de Euler:
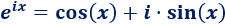
El logaritmo de \(-1\) es el valor \(x\) tal que \(e^x=-1\). Aplicando la fórmula anterior, queremos que se cumpla lo siguiente:

Puede servirnos \(x = \pi\):
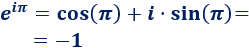
Por tanto,
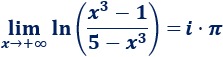
Límite 24
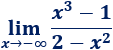
Resolvemos:
El límite es infinito porque el grado del polinomio del numerador es mayor. Ahora bien, hay que tener en cuenta que \(x\) tiende a \(-\infty\).
Cuando \(x\) tiene a \(-\infty\) el numerador tiende a \(-\infty\) (negativo al cubo). El denominador también tiende a \(-\infty\) porque tenemos negativo al cuadrado, pero con coeficiente negativo.
Por tanto,
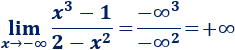
El exponente que hemos escrito al infinito es para indicar que el del numerador es de mayor orden.
Límite 25
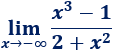
Resolvemos:
Razonando de forma similar al límite anterior, el resultado de este límite es infinito negativo:
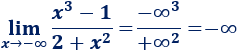
Límite 26
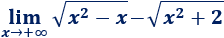
Límite 27
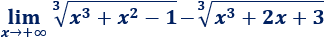
Límite 28
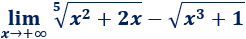
Límite 29
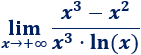
Límite 30
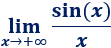
Límite 31
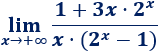
Límite 32
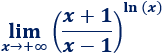
Límite 33
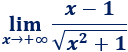
Límite 34
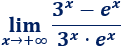
Límite 35
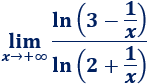
Límite 36
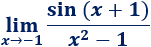
Ayuda: utilizad el siguiente límite:
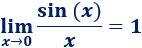
Límite 37

Ayuda: utilizad el siguiente límite:
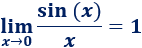
Límite 38
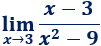
Límite 39
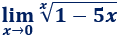
Límite 40
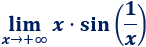
Límite 41
Demostrar el límite siguiente, que se ha empleado en varias ocasiones en esta página:
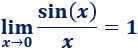
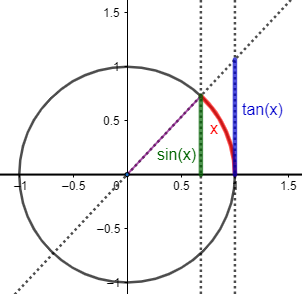
Ayuda: representación del coseno de \(x\), del arco de circunferencia con ángulo \(x\) y de la tangente de \(x\) en un circuncerencia de radio \(R=1\), siendo \(0< x < \pi/2\):
Límite 42
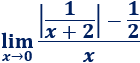
Límite 43
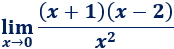
Límite 44
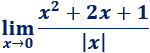
Límite 45
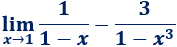
Límite 46
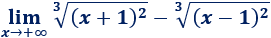
Límite 47

Límite 48
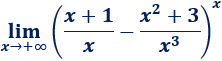
Límite 49
Comprobar la fórmula que empleamos para la indeterminación uno elevado a infinito (\(1^\infty\)):
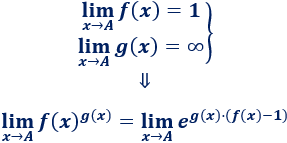
Límite 50