Cómo encontrar la ecuación de la parábola
En ocasiones necesitamos encontrar la ecuación de una parábola a partir de su gráfica o conociendo algunos de sus puntos (como el vértice o puntos de corte con el eje de abscisas), así que vamos a explicar varias propiedades que nos pueden ayudan a conseguirlo.
Índice:
- Función parábola
- Vértice de la parábola
- Raíces o puntos de corte
- Cómo obtener la ecuación
- Ejemplos o problemas resueltos
1. Función parábola
La función cuya gráfica es una parábola tiene la siguiente forma
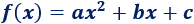
O bien, si escribimos la parábola como una ecuación,
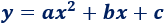
En ambos casos, siempre debe ser \(a \neq 0\).
En esta página proporcionamos ciertas características o propiedades de las parábolas que nos ayuden a encontrar los coeficientes \(a\), \(b\) y \(c\).
2. Vértice de la parábola
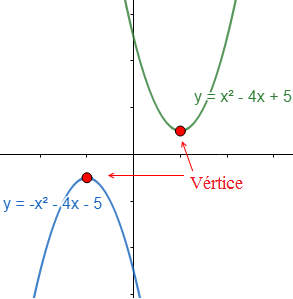
Todas las parábolas tienen forma de \(\cup\) (si \(a> 0\)) o de \(\cap\) (si \(a < 0\)). En cualquier caso, el punto más alto o máximo (si \(a> 0\)) o el punto más bajo o mínimo (si \( a< 0\)) de la parábola es el punto cuya primera coordenada es
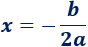
Ejemplo de una parábola con forma de \(\cup\) (verde) y otra con forma de \(\cap\) (azul):
3. Raíces o puntos de corte
Las raíces de la función parabólica son los \(\alpha\) tales que \(f(\alpha ) = 0\).
Los puntos \((\alpha ,0)\) de la parábola cortan al eje de abscisas. Una parábola puede tener 1, 2 o ningún punto de corte con este eje.
Ejemplo de una parábola con dos raíces (\(x = -1\) y \(x=1\)):
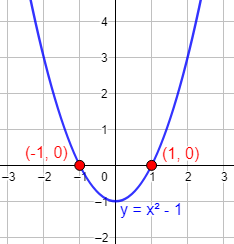
Nota: el número de puntos de corte depende de si las raíces son reales o complejas. En esta página sólo tendremos en cuenta las raíces reales.
Se pueden dar 3 casos.
Caso 1:
La parábola tiene dos raíces (reales) distintas: \(\alpha \) y \(\beta\). Entonces, se cumple la siguiente igualdad:
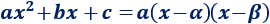
Caso 2:
La parábola tiene una única raíz (real): \(\alpha\). Entonces, se cumple que
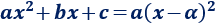
Caso 3:
La parábola no tiene raíces. En este caso, no podemos usar las raíces para encontrar la ecuación.
4. Cómo obtener la ecuación
Una forma de obtener la ecuación de la parábola es hacerlo resolviendo un sistema de 3 ecuaciones lineales a partir de 3 puntos distintos de la parábola (mirar Problema 5). Sin embargo, este método puede ser engorroso, así que es preferible utilizar las propiedades vistas anteriormente: coordenadas del vértice, puntos de corte, etc.
En los siguientes problemas veremos ejemplos de cómo hallar la ecuación de la parábola en diferentes situaciones.
5. Ejemplos o problemas resueltos
Problema 1
Encontrar la ecuación de la parábola que corta al eje de las abscisas en los puntos (1, 0) y (3, 0) y que pasa al eje de ordenadas en el punto (0, 9).
Solución:
De los puntos de corte con el eje de abscisas sabemos que las raíces de la función parabólica son \( x = 1\) y \(x = 3\). Por tanto, la ecuación de la parábola es
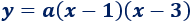
Falta conocer el coeficiente \(a\), pero podemos hallarlo sabiendo que la parábola pasa por el punto (0, 9). Sólo tenemos que sustituir las coordenadas:
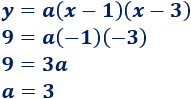
Por tanto, la ecuación de la parábola es
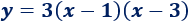
O bien, si calculamos los productos,

Gráfica:
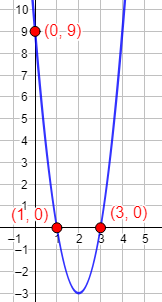
Problema 2
Hallar la ecuación de la parábola que tiene el vértice en el punto (1, 1) y que pasa por el punto (0, -3).
Solución:
Sabemos que la primera coordenada del vértice es
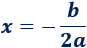
Por tanto, como el vértice está en (1, 1), tenemos
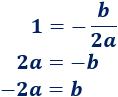
Por otro lado, podemos sustituir las coordenadas del punto (0, -3) en la ecuación general de la parábola:
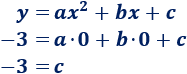
Sustituimos \(c=-3\) y \(b = -2a\) en la ecuación:
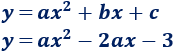
Nos falta hallar el coeficiente \(a\), pero también podemos sustituir las coordenadas del vértice (1, 1) en la ecuación:
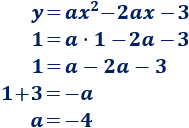
Luego la ecuación de la parábola es
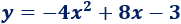
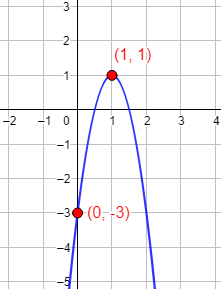
Gráfica:
Problema 3
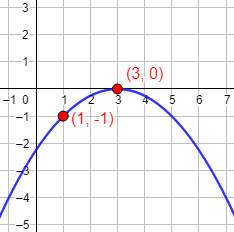
Hallar la función parabólica cuya única raíz es \(x = 3\) y cuya gráfica pasa por el punto (1, -1).
Solución:
Como la función tiene una única raíz \(x=-3\), la función tiene la forma
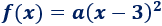
Sustituimos las coordenadas del punto (1, -1):
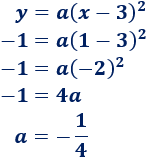
Por tanto,
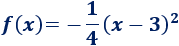
O bien,
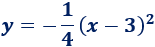
Si desarrollamos el cuadrado, tenemos
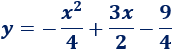
Gráfica:
Problema 4
Encontrar la ecuación de la parábola cuyo vértice se encuentra en (0, 1) y que corta al eje de abscisas al menos en \(x = -1\).
Solución:
Como no sabemos si hay una o varias raíces, sólo podemos usar el punto de corte para sustituir en la ecuación.
Gracias al vértice sabemos
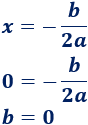
Por lo que
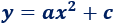
Sustituimos las coordenadas del vértice:
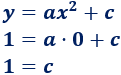
Por tanto,
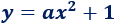
Finalmente, sustituimos las coordenadas del punto de corte (-1,0):
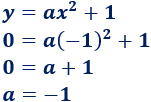
Luego la ecuación de la parábola es
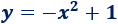
Gráfica:
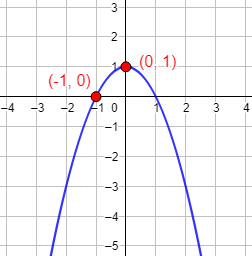
Problema 5 (sistema)
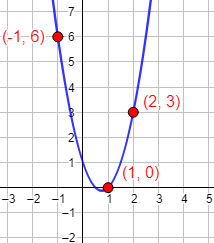
Hallar la ecuación de la parábola sabiendo que su gráfica pasa por los siguientes puntos: (1, 0), (-1, 6) y (2, 3).
Solución:
En este problema sólo conocemos tres puntos de la gráfica de la parábola, sin saber si alguno de ellos es el vértice. No tenemos más remedio que resolver un sistema de ecuaciones.
La ecuación de la parábola es
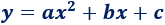
Sustituimos las coordenadas de los vértices en la ecuación:
Punto (1, 0):
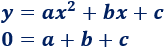
Punto (-1, 6):
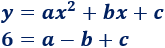
Punto (2, 3):
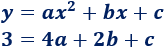
El sistema de ecuaciones que tenemos es
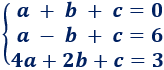
Podemos resolver el sistema por el método que deseemos. Su solución es
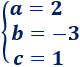
Por tanto, la ecuación de la parábola es
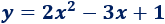
Gráfica: