Cómo dibujar la gráfica de una función
En esta página explicamos qué es la gráfica de una función y cómo representarla con la ayuda de algunos de sus puntos. También, mostramos algunos ejemplos de gráficas (función lineal, parabólica, cúbica, etc.) y explicamos cómo calcular los puntos de corte con los ejes. Se incluyen ejemplos, gráficas y problemas resueltos.
Índice:
- Concepto de gráfica y ejemplo
- Ejemplos de gráficas
- Puntos de corte
- Problemas resueltos
1. Concepto de gráfica y ejemplo
Dada una función \(y = f(x)\), su gráfica, \(gr(f)\), es el conjunto de puntos \((x,f(x))\), esto es, el conjunto de puntos cuya segunda coordenada es la imagen de la primera coordenada, siendo la primera coordenada un elemento del dominio de la función.
Matemáticamente,
$$ gr(f) := \{ (x,y)|y=f(x), \forall x\in Dom(f)\}$$
Ejemplo
Consideremos la función \(f(x) = 2x +1\).
Para calcular los puntos de la gráfica, damos valores a \(x\) y calculamos su imagen (sustituyendo). Es recomendable que usemos una tabla:
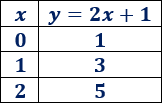
En la primera columna escribimos los valores que damos a \(x\) y en la segunda columna escribimos su imagen (se calcula sustituyendo en la función):
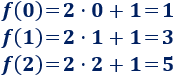
Cada número de la primera columna es la primera coordenada de un punto de la gráfica; y, cada uno de la segunda, la segunda coordenada.
Los tres puntos obtenidos son
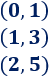
Para dibujar la gráfica de \(f\), representamos los puntos y los unimos:
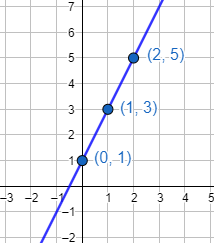
La gráfica de esta función es una recta.
2. Ejemplos de gráficas
Las gráficas de las funciones pueden ser muy variadas: rectas, parábolas, hipérbolas, etc. Veamos algunos ejemplos.
Función parabólica \(y = x^2\):
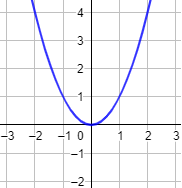
Función hiperbólica \(y = 1/x\):
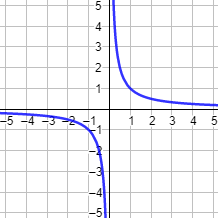
Función cúbica \(y = x^3-3x\):
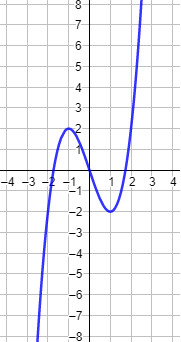
Función coseno \(y = cos(x)\):
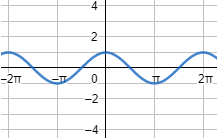
La forma de la gráfica de una función puede predecirse atendiendo a la expresión algebraica de dicha función.
Por ejemplo, las rectas siempre son funciones polinómicas de grado \(1\):
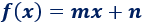
Y, las parábolas, son polinómicas de grado \(2\):
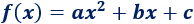
siendo, \(m\neq 0\) y \(a\neq 0\).
Más información de estas funciones en
3. Puntos de corte
Los puntos de corte de una función con los ejes son los puntos donde la gráfica corta o atraviesa los ejes de coordenadas.
Ejemplo
En rojo, los puntos de corte de la función \(f(x) = x^3-3x+2\):
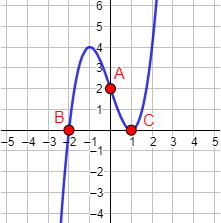
El punto A es el punto de corte con el eje de ordenadas (eje Y) y los puntos B y C son los puntos de corte con el eje de abscisas (eje X).
No todas las funciones tienen puntos de corte. De haberlos, sólo puede haber un punto de corte con el eje Y; mientras que puede haber varios puntos de corte con el eje X.
Calcular el punto de corte con Y
Si lo hay, el punto de corte con el eje Y siempre es el punto cuya primera coordenada es \(0\) y cuya segunda coordenada es \(f(0)\).
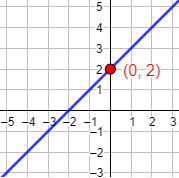
Por ejemplo, la función \(f(x) = x +2\) corta al eje Y en el punto
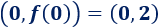
Gráfica:
Calcular el punto de corte con X
Si los hay, son la o las soluciones de la ecuación \(f(x)=0\).
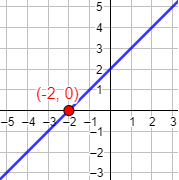
Por ejemplo, la función \(f(x) = x +2\) sólo corta al eje X en un punto porque la ecuación \(x+2=0\) sólo tiene una solución. Como dicha solución es \(x = -2\), el punto de corte es \((-2,0)\):
Las rectas siempre cortan al eje Y en un punto. Si cortan al eje X, lo hacen en un único punto.
4. Problemas resueltos
Problema 1
Representar las gráficas de las siguientes rectas:
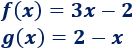
¿Los puntos \((1,1)\) y \((2,4)\) pertenecen a la gráfica de alguna de ellas?
Solución:
Como las funciones son rectas, es suficiente con calcular dos puntos y unirlos. Nosotros usaremos \(x=0\) y \(x=3\).
Primera función
Calculamos dos puntos:
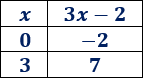
Representamos los dos puntos y los unimos:
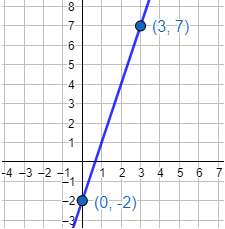
Segunda función
Calculamos dos puntos:
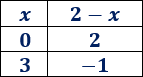
Representamos los dos puntos y los unimos:
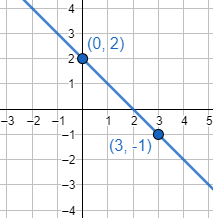
Observando ambas gráficas, el punto \((1,1)\) forma parte de las graficas de \(f\) y de \(g\), pero el punto \((2,4)\) sólo pertenece a la gráfica de \(f\).
Problema 2
Representar la gráfica de la siguiente parábola:
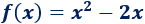
Ayuda: el vértice de la parábola es \((1,-1)\).
Solución:
Como se trata de una parábola, es mejor calcular más de dos puntos. Usamos \(x = -1\), \(x=0\) y \(x=2\):
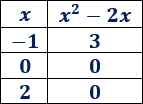
Representamos los tres puntos y el vértice y los unimos:
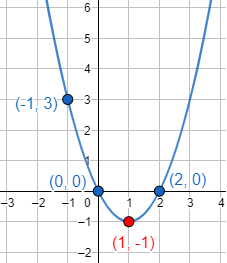
El punto rojo es el vértice de la parábola. El vértice siempre es el pico de la gráfica.
Problema 3
Calcular los puntos de corte con los ejes de la siguiente recta:
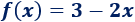
Solución:
Punto de corte con Y
Tenemos que calcular la imagen de \(0\):
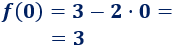
Es el punto \((0,3)\).
Punto de corte con X
Resolvemos la ecuación \(f(x)=0\):
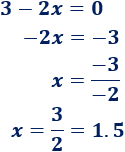
Es el punto \((1.5,0)\).
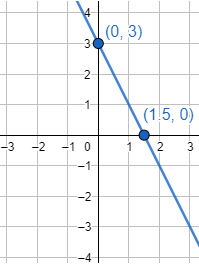
Como se trata de una recta, podemos representar su gráfica con la ayuda de los dos puntos calculados:
Problema 4
Calcular los puntos de corte con los ejes de la siguiente parábola:
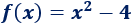
Ayuda: el vértice está sobre el eje Y.
Solución:
Corte con el eje Y
Tenemos que calcular la imagen de \(0\):
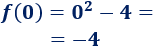
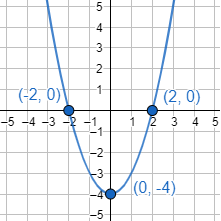
Por tanto, es el punto \((0,-4)\).
Corte con el eje X
Tenemos que resolver una ecuación de segundo grado incompleta:
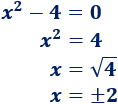
Por tanto, hay dos puntos de corte con el eje X:
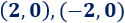
Representamos la gráfica:
Problema 5
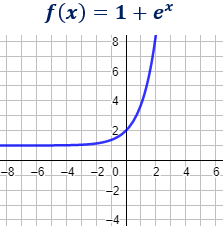
Determinar, observado la gráfica, los puntos de corte con los ejes de la siguiente función:
Solución:
Observando la gráfica, sólo corta al eje Y y lo hace en el punto \((0,2)\). No corta al eje X.
Se trata de una función exponencial.
Más problemas similares: primeras gráficas.