Problemas de funciones
Resolvemos problemas de aplicación de funciones. Habilidades que necesitamos:
-
Plantear funciones
-
Interpretar y representar gráficas
-
Aplicar las funciones (calcular imágenes o antiimágenes)
Problemas para secundaria y bachillerato.
Problema 1
La siguiente función proporciona la distancia (en kilómetros) que recorre una moto a una velocidad de \(100km/h\) en función del tiempo \(t\) (en horas):
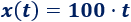
-
¿Qué distancia recorre en \(2\) horas? ¿Y en \(5\) horas?
-
¿Cuánto tiempo debe circular para recorrer \(5\) kilómetros?
Solución
a. Tenemos que calcular la imagen de \(2\) y de \(5\):
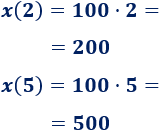
En \(2\) horas recorre \(200\) kilómetros y en \(5\) horas, \(500\).
b. Tenemos que calcular \(t\) tal que \(x(t) = 5\):
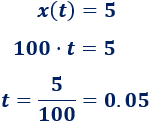
Tarda \(0.05\) horas en recorrer \(5km\), es decir, \(3\) minutos.
Problema 2
La siguiente función proporciona los días necesarios para construir un coche en función del número de operarios que trabajen:
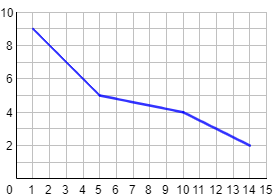
-
¿Cuántos días se necesitan si trabajan \(3\) operarios? ¿Y si trabajan \(5\) operarios? ¿Y si trabajan \(12\) operarios?
-
¿Cuántos operarios se necesitan para construir el coche en \(4\) días? ¿Y en \(8\) días?
-
¿Se trata de una función lineal? ¿Por qué?
Solución
a. Observando la gráfica,
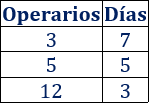
b. Para construirlo en \(4\) días, se necesitan \(10\) operarios. Para hacerlo en \(8\) días, se necesitan \(2\).
c. No. Las gráficas de las funciones lineales son rectas. La gráfica de este problema está formada por tres segmentos de rectas con distinta pendiente.
Problema 3
La compañía telefónica de Roberto le cobra \(10€\) mensuales de cuota y \(0.05€\) por cada minuto de llamada.
-
Calcular la función que proporciona el coste de la factura mensual de Roberto en función del número de minutos de llamada.
-
¿Cuál sería el coste de un mes en el que ha realizado \(50\) minutos de llamada? ¿Y si son \(150\) minutos?
-
Si la factura del mes de junio fue de \(20€\), ¿cuánto minutos de llamada realizó Roberto?
Solución
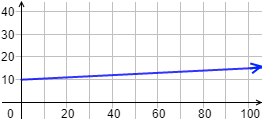
a. Si Roberto realiza llamadas con un total de \(x\) minutos, el coste de estas llamadas sería \(0.05·x\). Además de esto, hay que sumar \(10€\) de la cuota.
Por tanto, la función es

b. Si en un mes realiza \(50\) minutos de llamadas, la factura de dicho mes será de \(12.5€\):
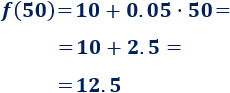
Si son \(150\) minutos, será de \(17.5€\):
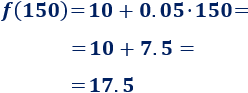
c. Tenemos que calcular \(x\) tal que \(f(x) = 20\):
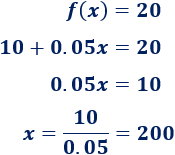
En el mes de junio realizó \(200\) minutos de llamada.
Gráfica de la función:
Problema 4
Una fábrica de bolígrafos calcula el coste de fabricación (en euros) mediante la siguiente función:
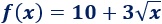
siendo \(1\leq x\leq 1600\) el número de unidades.
-
¿Cuánto cuesta un pedido de \(9\) bolígrafos? ¿Y uno de \(100\)? ¿Y uno de \(1600\)?
-
¿Cuál es el precio de cada bolígrafo en cada uno de los pedidos anteriores?
Solución
a. Tenemos que calcular la imagen de \(9\), \(100\) y \(1600\):
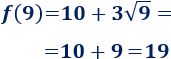
El pedido de \(9\) bolígrafos cuesta \(19€\).
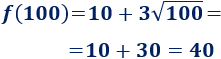
El pedido de \(100\) bolígrafos cuesta \(40€\).
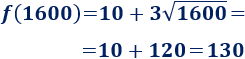
El pedido de \(1600\) bolígrafos cuesta \(130€\).
b. Para calcular el precio de cada bolígrafo, dividimos el precio total entre el número de bolígrafos.
En el pedido de \(9\) bolígrafos el precio es de \(2.11€\):
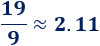
En el pedido de \(100\) bolígrafos el precio es de \(0.4€\):
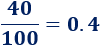
En el pedido de \(1600\) bolígrafos el precio es de \(0.08€\):
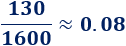
Cuanto mayor sea el pedido, más barato es el precio unitario de los bolígrafos.
Gráfica de la función:
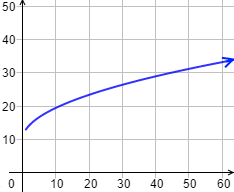
Problema 5
Para construir una ventana cuadrada se necesitan \(4\) barras de aluminio iguales y un cristal. El precio de las barras de aluminio es de \(10€/m\) y el del cristal es de \(20€/m^2\).
-
Calcular la función que proporciona el coste de una venta cuadrada en función de la longitud del lado.
-
¿Cuál es el coste de una ventana de lado \(3m\)? ¿Y de lado \(5m\)?
Solución
a. Si el lado de la ventana mide \(x\) metros, se necesitan \(4·x\) metros de aluminio y un cristal de \(x^2\) metros cuadrados.
Por tanto, el coste de la venta viene dado por
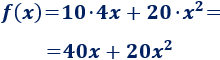
b. El coste de una ventana de \(3m\) de lado es de \(300€\):
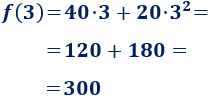
Y el de una ventana de \(5m^2\) es de \(700€\):
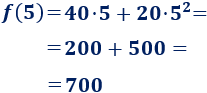
Problema 6
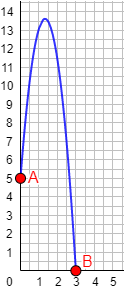
La siguiente gráfica muestra la altura con respecto del suelo (en metros) en función del tiempo (en minutos) de un balón desde que se lanza hacia el cielo (A) hasta que cae al suelo (B):
Es la gráfica de la función
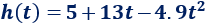
-
¿Desde qué altura se lanza el balón?
-
¿Qué altura aproximada alcanza el balón y en cuánto tiempo?
-
¿Cuánto tarda el balón en caer al suelo desde que se lanza?
-
¿Cuál es la altura del balón a los dos minutos de su lanzamiento? ¿Y en el minuto \(0.653\)?
Solución
a. El balón se lanza en \(t=0\), es decir, a \(5\) metros de altura.
b. La mayor altura que alcanza es aproximadamente \(13.62\) metros. Tarda aproximadamente \(1.33\) minutos en hacerlo.
c. El balón cae al suelo cuando su altura es \(0\). Tarda \(3\) minutos en caer.
d. Para calcular la altura exacta, utilizamos la función:
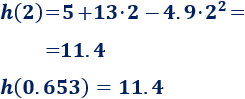
Es decir, en el minuto \(0.653\) y en el minuto \(2\), el balón se encuentra a \(11.4\) metros del suelo (cuando sube y cuando cae).
Problema 7
Se desea construir un depósito de agua con forma cilíndrica de radio \(r\) y de altura \(2·r\).
-
Hallar la función que proporciona el volumen del depósito en función de su radio.
-
¿Cuáles deben ser las dimensiones del depósito para que su capacidad sea \(100\) litros?
Solución
Recordad que el volumen de un cilindro es

Y que \(1L\) de agua equivale a \(1dm^3\).
a. Como la altura es \(h = 2r\), la función volumen del depósito es
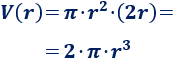
b. Como \(100\) litros son \(100 dm^3\), tenemos que resolver la siguiente ecuación:
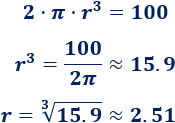
El radio debe medir, aproximadamente, \(2.51 dm\). Por tanto, la altura debe ser \(5.02dm\).
Problema 8
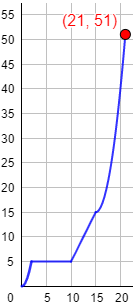
La siguiente gráfica muestra la población (en millones) en función del año (en siglos) desde el año \(0\) al siglo \(XXI\) de una isla europea:
-
¿Cuál era la población en el siglo \(V\)? ¿Y en los siglos \(VII\), \(X\), \(XV\) y \(XX\)?
-
Aproximadamente, ¿qué población había en el año \(2000\)? ¿Y en el año \(1150\)?
-
¿Fue mayor el crecimiento entre los siglos \(X\) y \(XV\) o entre los siglos \(XV\) y \(XX\)?
-
¿De qué tipo de función se trata?
Solución
a.
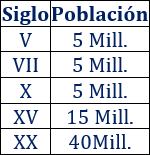
b. El año \(2000\) es el siglo \(XXI\). Había \(51\) millones de habitantes.
El año \(1150\) es la mitad del siglo \(XII\). Había aproximadamente \(10\) millones de habitantes.
c. El crecimiento entre los siglos \(X\) y \(XV\) fue de \(10\) millones. Entre los siglos \(XV\) y \(XX\), \(25\) millones. Por tanto, el crecimiento fue mayor entre los siglos \(XV\) y \(XX\).
d. Se trata de una función segmentada: las dos partes centrales son funciones lineales y las dos partes laterales son parabólicas.
Problema 9
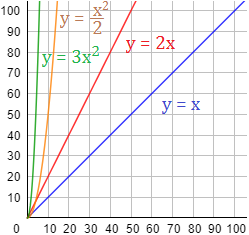
A continuación, se proporcionan las gráficas de cuatro funciones:
-
¿Cuáles son parabólicas y cuáles son lineales?
-
De las parabólicas, ¿cuál de ellas crece más rápidamente? ¿Y de las lineales?
-
Como regla general, ¿crecen más rápido las funciones parabólicas o las lineales?
-
¿Qué pendiente tienen las funciones lineales?
-
Calcular la imagen de \(x = 10\) de las cuatro funciones.
Solución
a. Las parabólicas son las que tienen \(x^2\):
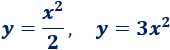
Las lineales no tienen \(x^2\):
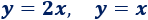
b. De las parabólicas, crece más rápido la que tiene el coeficiente \(3\). De las lineales, la que tiene el coeficiente \(2\).
c. Como regla general, crecen más rápido las funciones parabólicas.
d. La pendiente de una función lineal es el coeficiente de la \(x\): \(2\) (la roja) y \(1\) (la azul).
e. Sólo tenemos que sustituir \(x=10\):
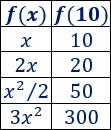
Problema 10
Representar la siguiente función definida por partes:
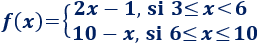
-
¿Cuál es la imagen de \(x = 6\)?
-
¿Cuál es el dominio de la función?
-
¿Cuál es la imagen de la función?
-
¿Es una función continua? ¿Cuáles son sus puntos de discontinuidad?
Solución
a. Para calcular la imagen de \(x=6\), tenemos que utilizar la segunda expresión algebraica:
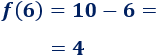
b. El dominio de la función son los valores que puede tomar la variable \(x\). Es el intervalo cerrado \([3, 10]\).
c. Para calcular la imagen (el o los intervalos de los valores que toma \(f\)) es más fácil si representamos la gráfica:
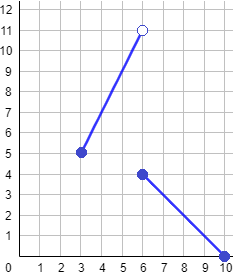
La imagen de \(f\) en el intervalo \([3,6)\) es el intervalo \([5, 11)\).
La imagen de \(f\) en el intervalo \([6,10]\) es el intervalo \([0, 4]\).
Por tanto, la imagen de la función es la siguiente unión de intervalos:
![[0,4] U [5,11) Problemas resueltos de funciones: plantear funciones, representar e interpretar gráficas, calcular imágenes y antiimágenes. Problemas de aplicación. Matemáticas.](https://www.problemasyecuaciones.com/funciones/problemas/P10-2.png)
d. No es una función continua porque no podemos representar su gráfica de un solo trazo. El punto de discontinuidad es \(x = 6\) (donde hay un salto).
La función es continua en los otros puntos del dominio.
Más problemas similares: Problemas resueltos de funciones.
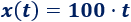

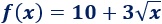

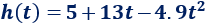



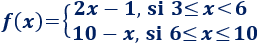
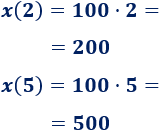
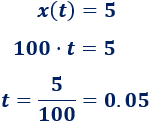


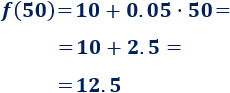
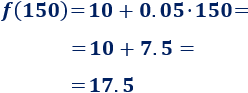
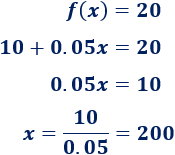

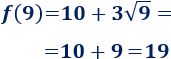
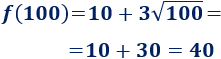
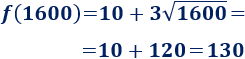
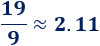
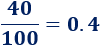
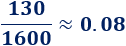

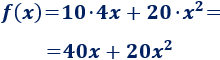
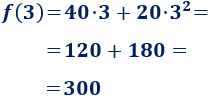
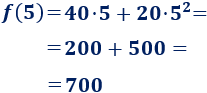
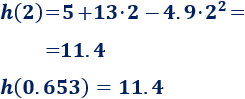

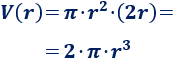
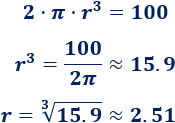

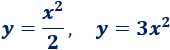
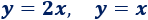
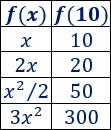
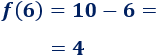

![[0,4] U [5,11) Problemas resueltos de funciones: plantear funciones, representar e interpretar gráficas, calcular imágenes y antiimágenes. Problemas de aplicación. Matemáticas.](https://www.problemasyecuaciones.com/funciones/problemas/P10-2.png)