Función polinómica
Explicamos el concepto de función polinómica y las características básicas de las funciones polinómicas de primer, segundo y tercer grado (con ejemplos y gráficas) y resolvemos algunos problemas relacionados.
Índice:
- Definición formal
- Función constante
- Función lineal
- Función cuadrática
- Función cúbica
- Propiedades
- Problemas resueltos
1. Definición formal
La forma general de una función polinómica de grado \(n\in\mathbb{N}\) es
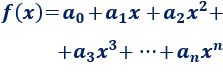
siendo \(a_n\neq 0\).
Los términos \(a_k\) se denominan coeficientes y \(a_n\) es el coeficiente principal.
También, podemos escribir la forma general como
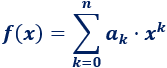
El dominio de una función polinómica es el conjunto de todos los reales.
2. Función constante
Una función polinómica de grado \(0\) se denomina función constante y su forma general es
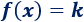
La gráfica de una función constante es una recta horizontal (paralela al eje de abscisas).
Corta el eje de ordenadas en un punto: \((0,k)\). Sólo corta al eje de abscisas si \(k=0\), en cuyo caso coincide con el eje.
Ejemplo
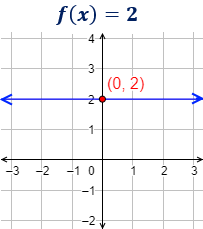
El punto de corte con el eje de ordenadas es \((0,2)\). No corta al eje de abscisas.
3. Función lineal
Una función polinómica de grado \(1\) se denomina función lineal y tiene la forma general
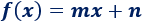
El coeficiente \(m\) se denomina pendiente y el coeficiente \(n\), ordenada en el origen.
La gráfica de una función lineal es una recta oblicua (recta no horizontal ni vertical).
Corta al eje de ordenadas en el punto \((0,n)\). También, corta al eje de abscisas en un punto.
Ejemplo
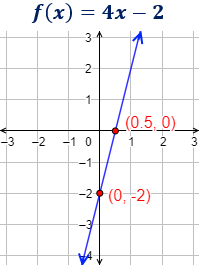
La recta es creciente (de izquierda a derecha) porque la pendiente \(m=4\) es positiva.
El punto de corte con el eje de abscisas es \((0.5,0)\) y con el eje de ordenadas es \((0,-2)\).
Más información y ejemplos en función lineal.
4. Función cuadrática
Una función polinómica de grado \(2\) se denomina función cuadrática y tiene la forma general
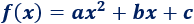
La gráfica es una parábola. Tiene forma de \(\cup\) si \(a>0\) y forma de \(\cap\) si \(a< 0\).
Una función cuadrática corta al eje de ordenadas en el punto \((0,c)\).
Puede cortar al eje de abscisas en dos, uno o ningún punto, dependiendo del número de soluciones reales de la ecuación cuadrática asociada, \(ax^2+bx+c=0\).
Toda función cuadrática presenta un extremo absoluto (máximo o mínimo) en
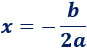
Este extremo se denomina vértice.
Ejemplo
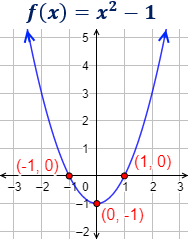
El punto de corte con el eje de ordenadas es \((0,-1)\). El vértice de la parábola también es \((0,-1)\).
Los puntos de corte con el eje de abscisas son \((-1,0)\) y \((1,0)\). Observad que las primeras coordenadas son \(x=-1\) y \(x=1\), que son las soluciones de la ecuación cuadrática \(x^2-1=0\).
Más información y ejemplos en función cuadrática.
5. Función cúbica
Una función polinómica de grado \(3\) se denomina función cúbica y tiene la forma general
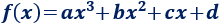
La gráfica es una curva cúbica.
Corta al eje de ordenadas en el punto \((0,d)\).
Puede cortar al eje de abscisas en tres, dos o un punto, dependiendo de las soluciones de la ecuación cúbica asociada.
Ejemplo
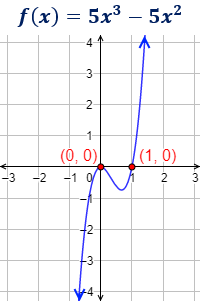
Los puntos de corte con el eje de abscisas son \((0,0)\) y \((1,0)\).
El punto de corte con el eje de ordenadas es \((0,0)\).
6. Algunas propiedades
- Excepto la función constante (grado \(0\)), las funciones polinómincas tienden a infinito cuando \(x\) crece o decrece indefinidamente. El signo del infinito depende del coeficiente principal y del grado del polinomio.
- Si el grado es mayor que \(1\), no tienen asíntotas.
- Si el grado es \(1\), la función es una recta y ella misma es la asíntota (oblicua).
- Si el el grado es \(0\), la función es una recta horizontal y ella misma es su asíntota (horizontal).
7. Problemas resueltos
Problema 1
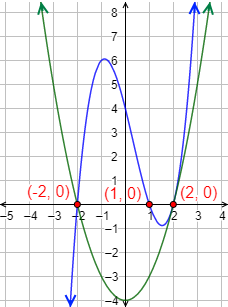
Hallar una función cuadrática, \(f\), que corte al eje de abscisas en los puntos \(A=(1,0)\) y \(B=(2,0)\) y una función lineal, \(g\), que pase por el punto \(B\) y por el punto de corte de \(f\) con el eje de ordenadas.
Solución:
La siguiente función cuadrática tiene los puntos de corte \(A\) y \(B\):
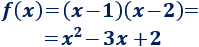
Corta al eje de ordenadas en el punto
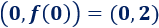
Para hallar una función lineal que pase por el punto \(B\) y el punto \((0,2)\), sólo tenemos que sustituir las coordenadas de estos puntos en la forma general de la función y resolver el sistema:
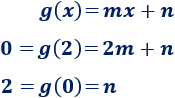
La solución del sistema es \(n=2\) y \(m=-1\), así que se trata de la recta
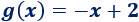
Gráficas:
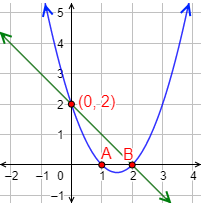
Problema 2
La forma canónica de una ecuación cuadrática es
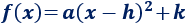
siendo \((h,k)\) el punto de su vértice.
Hallar la forma canónica de la siguiente función:
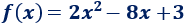
Solución:
Los coeficientes son \(a=2\), \(b=-8\) y \(c=3\).
La primera coordenada del vértice es
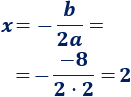
Calculamos la segunda coordenada:
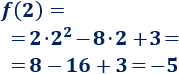
El vértice es \((2,-5)\).
Por tanto, la forma canónica es
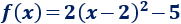
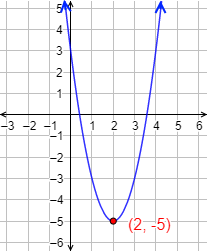
Gráfica:
Problema 3
Hallar una función cuadrática y una función cúbica en forma general que tengan, al menos, los dos siguientes puntos de corte con el eje de abscisas:
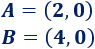
Solución:
Una posible función cuadrática es
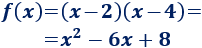
Y una cúbica,
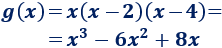
Esta función cúbica también tiene el punto de corte \((0,0)\).
Gráficas:
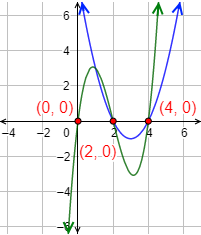
Problema 4
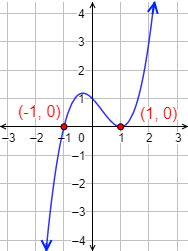
Hallar la forma general de una función cúbica cuyos dos únicos puntos de corte con el eje de abscisas sean \((-1,0)\) y \((1,0)\).
Solución:
Sólo tenemos que hacer que una de las soluciones sea doble y la otra sea simple:
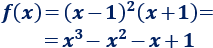
Gráfica:
Problema 5
Hallar una función cúbica que tenga los mismos puntos de corte con el eje de abscisas que \(x^2-4\) y el punto de corte \((1,0)\).
Solución:
Podemos escribir la función cuadrática como
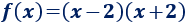
Sólo tenemos que añadir el factor \(x-1\):
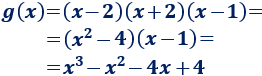
Gráficas: