Función par y función impar
Definimos función par y función impar y resolvemos algunos problemas. Se incluyen ejemplos y gráficas.
Índice:
- Función par
- Función impar
- Problemas resueltos
1. Función par
Una función \(f\) es par si
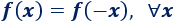
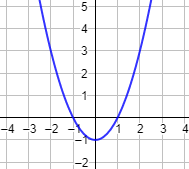
Las gráficas de las funciones pares presentan simetría respecto al eje de ordenadas.
Ejemplo
La siguiente función es par:
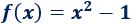
Demostración:
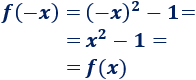
Gráfica:
2. Función impar
Una función \(f\) es impar si
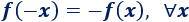
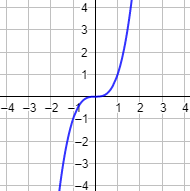
Las gráficas de las funciones impares presentan simetría rotacional con respecto al origen. Es decir, la gráfica no cambia si se rota 180°.
Ejemplo
La siguiente función es par:
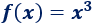
Demostración:
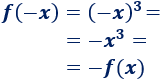
Gráfica:
Podéis encontrar algunas propiedades de las funciones pares e impares en paridad de funciones.
4. Problemas resueltos
Problema 1
Determinar si las siguientes funciones son pares o impares:
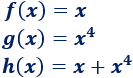
Solución:
La función \(f\) es impar:
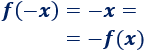
La función \(g\) es par:
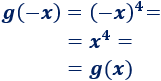
La función \(h\) no es par ni impar. Por ejemplo,
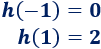
Problema 2
Determinar si las siguientes funciones son pares o impares:
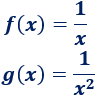
Solución:
La función \(f\) es impar:
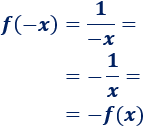
La función \(g\) es par:
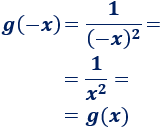
Problema 3
¿Existe alguna función que sea par e impar?
Solución:
Supongamos que \(f\) es par:
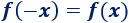
Supongamos que \(f\) también es impar:
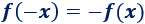
Usando ambas definiciones, tenemos
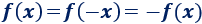
Es decir,
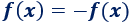
Operamos un poco:
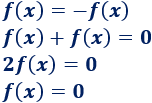
Por tanto, la única función que es par e impar es la función nula.
Problema 4
Determinar si es par o impar la función cuya gráfica es la siguiente:
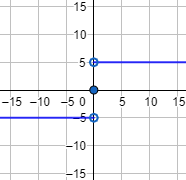
Solución:
Hay simetría rotacional, así que se trata de una función impar.
Se trata de la siguiente función definida a trozos:
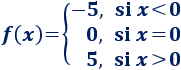
Problema 5
Determinar si las funciones seno y coseno son pares o impares.
Solución:
La función coseno es par. Su gráfica es
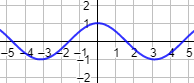
La función seno es impar. Su gráfica es
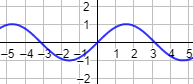
Más problemas similares: paridad de funciones.