Dominio y recorrido de funciones
Definimos qué es el dominio y el recorrido de una función, damos ejemplos y resolvemos 5 problemas.
Índice:
- Introducción
- Definiciones y ejemplos
- Casos generales
- Problemas resueltos
1. Introducción
Recordad que una función matemática \(f\) relaciona cada número \(a\) de un conjunto \(A\) con un único número \(b=f(a)\) de otro conjunto, \(B\). Esto se expresa mediante \(f \colon A \rightarrow B\).
Ejemplo
La siguiente función relaciona cada número entero (0, 1, -1, 2, -2, 3, -3,...) con su valor absoluto:
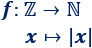
Por ejemplo,
-
La imagen de \(-1\) es \(1\):
-
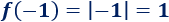
La imagen de \(1\) es \(1\):
-
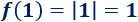
La imagen de \(-2\) es \(2\):
-
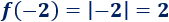
La imagen de \(-5\) es \(5\):
-
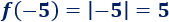
La imagen de \(0\) es \(0\):
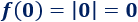
Gráfica:
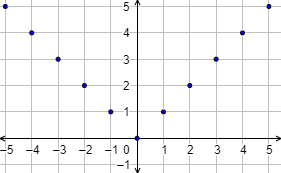
La función \(f\) está definida sobre los números enteros, \(\mathbb{Z}\). Este conjunto es el dominio de la función.
El conjunto de las imágenes del dominio es el conjunto de los números naturales (0, 1, 2, 3,...), \(\mathbb{N}\). Este conjunto es la imagen, el recorrido o el rango de la función.
Nota: la función valor absoluto también puede definirse sobre todos los reales, los enteros, los racionales o cualquier subconjunto los números complejos.
2. Definiciones y ejemplos
El dominio de una función es el conjunto sobre el que se define la función.
La imagen, recorrido o rango de una función es el conjunto de las imágenes de los elementos de su dominio.
En una función \(f \colon A \rightarrow B\), \(A\) es el dominio y \(B\) es el recorrido.
Muchas veces, por simplificar, se proporcionan un dominio y un recorrido genéricos. En este caso, se llama codominio al recorrido genérico y este conjunto contiene como subconjunto al recorrido de la función. Veamos un ejemplo:
Ejemplo
Sea la función racional
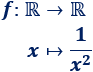
Gráfica:
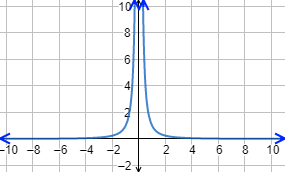
Esta función se ha definido sobre los números reales pero, en realidad, la función no está definida en todos los reales. Más exactamente, la función no está definida en \(0\) porque no se puede calcular su imagen: \(f(0) = 1/0\).
El dominio de esta función es todos los reales excepto \(0\):
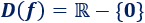
Además de esto, ninguna imagen es negativa ni \(0\) (puesto que el inverso del cuadrado de un número no nulo es siempre positivo). La imagen de la función son los números reales positivos:
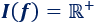
El recorrido de una función es un subconjunto del codominio, aunque pueden coincidir.
3. Casos generales
Cada función tiene un dominio y un recorrido distintos, pero tenemos algunas reglas generales:
-
El dominio y la imagen de una función polinómica es el conjunto de los reales.
-
El dominio de un logaritmo es el conjunto de los reales que hacen su argumento positivo.
-
El dominio de una función racional es el conjunto de los reales excepto los números que anulan el denominador.
-
El dominio de una raíz de orden par es el conjunto de los reales que hacen su radicando no negativo. El recorrido es un subconjunto de los reales no negativos.
Ejemplo
Sea la función raíz cuarta:
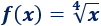
Como el orden de la raíz es par, su dominio y su imagen es
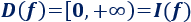
Gráfica:
4. Problemas resueltos
Nota: recomendamos, por ser más fácil, representar la gráfica de la función para calcular la imagen.
Problema 1
Determinar el dominio y la imagen de las siguientes funciones:
-
\(f(x) = 2x^3 - 1 \)
-
\( g(x) = \frac{1}{x-1}\)
-
\( h(x) = \frac{x}{x^2-1}\)
-
\( q(x) = e^x \)
Solución:
-
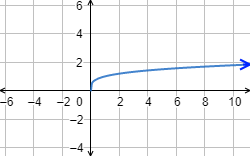
\(f(x) = 2x^3 - 1 \)
Como se trata de una función polinómica, tanto su dominio como su recorrido es el conjunto de los números reales.
Gráfica:
-
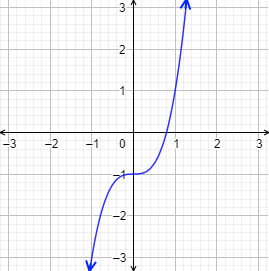
\( g(x) = \frac{1}{x-1}\)
Como es racional, el denominador no puede ser \(0\). Esto ocurre cuando \(x = 1\). Por tanto, el dominio es todos los reales excepto \(1\):
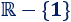
Para el recorrido, es más fácil si representamos la gráfica de la función:
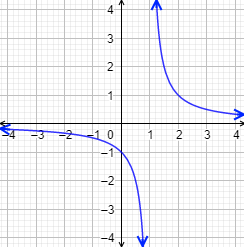
El recorrido es todos los reales excepto el \(0\). La función se aproxima a \(0\) cuando \(x\) crece o decrece indefinidamente, pero nunca llega a tomar dicho valor. Luego el recorrido es
-
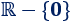
\( h(x) = \frac{x}{x^2-1}\)
Como la función es racional, el denominador no puede ser \(0\). Hallamos los puntos para los cuales el denominador es \(0\) resolviendo la siguiente ecuación cuadrática incompleta:
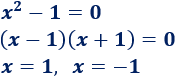
Por tanto, el dominio es todos los reales excepto \(1\) y \(-1\):
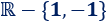
La gráfica de la función es
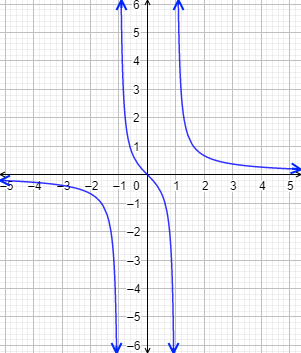
El recorrido es el conjunto de los números reales (incluido el \(0\)).
-
\( q(x) = e^x \)
Se trata de una función exponencial. Su dominio es el conjunto de los números reales. Su imagen es todos los reales positivos.
Gráfica:
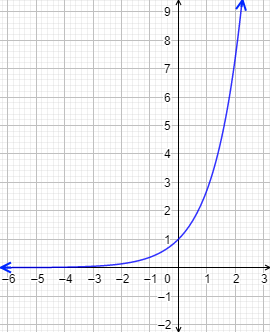
Problema 2
Determinar el dominio y la imagen de la siguiente función:
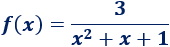
Solución:
Como es una función racional, el dominio es el conjunto de los reales excepto los puntos que anulan el denominador. Buscamos dichos puntos resolviendo la siguiente ecuación cuadrática completa:
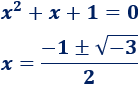
La ecuación no tiene soluciones (reales). Por tanto, el denominador siempre es distinto de \(0\).
El dominio es el conjunto de todos los reales.
Representamos la gráfica:
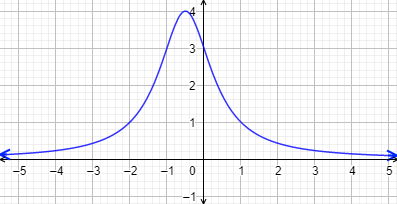
La función nunca llega a tomar el valor \(0\).
El valor más grande que toma es 4, que es la imagen del punto \(x = -0.5\):
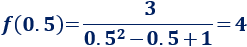
El recorrido la función es el siguiente intervalo:
Problema 3
Determinar el dominio y la imagen de la función cuya gráfica es la siguiente:
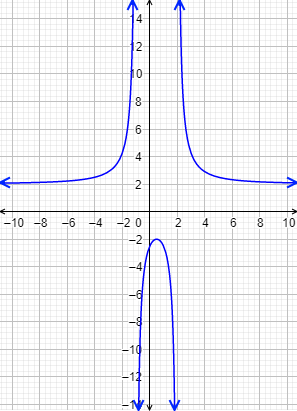
Solución:
El dominio es todos los reales excepto los puntos 2 y -1:
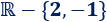
La función toma valores superiores a 2 y valores inferiores o iguales que -2. Por tanto, su imagen es una unión de dos intervalos:
Problema 4
Determinar el dominio y la imagen de la siguiente función:
Solución:
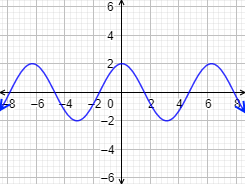
El dominio es todos los reales.
La función coseno toma todos los valores del intervalo [-1,1]. Como el coseno está multiplicado por 2, la imagen de esta función es el intervalo [-2,2].
Gráfica de la función:
Problema 5
Determinar el dominio y la imagen de la función cuya gráfica es la siguiente:
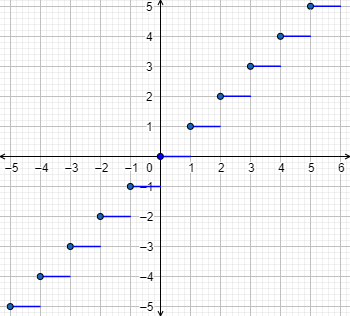
Calcular las imágenes de 1.3, 2.6, 3.1, -0.3 y -4.4.
Solución:
El dominio es todos los reales.
La imagen es el conjunto de los números naturales, \(\mathbb{N}\).
Se trata de la función parte entera: \(f(x) = [x]\).
Calculamos las imágenes:
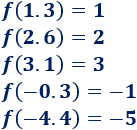
Más problemas similares en Dominio y recorrido.