Máximos y mínimos
de una función
Definimos extremos relativos y absolutos de una función y enunciamos las reglas de la primera y segunda derivada. Proporcionamos ejemplos y resolvemos algunos problemas.
La regla de la primera derivada proporciona los puntos candidatos a ser extremo relativo y la regla de la segunda derivada nos indica si un candidato es o no un extremo.
Índice:
- Definición de extremo
- Regla de la primera derivada
- Regla de la segunda derivada
- Problemas resueltos
1. Definición de extremo
Intuitivamente, un punto \(a\) es un máximo relativo de la función \(f\) si \(f(a)\geq f(x)\) para los \(x\) cercanos a \(a\). Es un mínimo relativo si \(f(a)\leq f(x)\).
Ejemplo
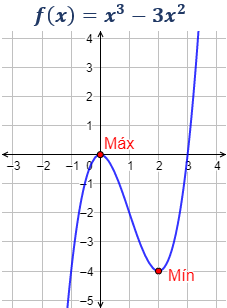
La función tiene un máximo relativo en \((0,0)\) y un mínimo relativo en \((2,-4)\).
Observad que \(x=0\) es un máximo en los puntos de su alrededor, pero no en todos, ya que, por ejemplo,

Definición formal:
Sea \(f: \mathbb{R} \rightarrow \mathbb{R}\) una función y sea \(a\in\mathbb{R}\), entonces
-
\(a\) es un mínimo relativo de \(f\) si existe \(\varepsilon > 0\) tal que
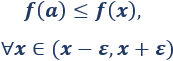
-
\(a\) es un máximo relativo de \(f\) si existe \(\varepsilon > 0\) tal que
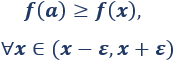
-
\(a\) es un extremo relativo de \(f\) si es un mínimo relativo o un máximo relativo.
Extremos absolutos:
Si \(a\) es un mínimo (o un máximo) para todo \(x\) del dominio de \(f\), se dice que es un mínimo absoluto (o un máximo absoluto).
Formalmente,
-
\(a\) es un mínimo absoluto de \(f\) si

-
\(a\) es un máximo absoluto de \(f\) si

-
\(a\) es un extremo absoluto de \(f\) si es un mínimo absoluto o un máximo absoluto.
Nota: observad que un extremo absoluto cumple la definición de extremo relativo.
Ejemplo
Los extremos de la función del ejemplo anterior no son absolutos.
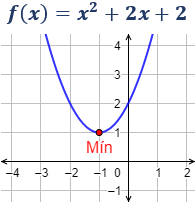
El vértice de una parábola siempre es un extremo absoluto. Por ejemplo, la siguiente parábola tiene un mínimo relativo en \((-1,1)\):
2. Regla de la primera derivada
Si la función \(f\) es derivable en \(c\) y \(f'(c)=0\), decimos que \(c\) es un punto crítico.
Los puntos críticos son los candidatos a ser extremos relativos (y absolutos).
Regla de la primera derivada:
Si \(f\) es derivable en el intervalo \(I=(a,b)\), entonces
-
\(f\) es creciente en \(I\) si
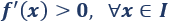
-
\(f\) es decreciente en \(I\) si
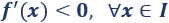
Por tanto, los candidatos para ser extremos son los puntos que anulan la derivada.
Demostración en Criterio de la primera derivada.
Aplicación de la regla:
Supongamos que \(f\) es derivable en \(I=(a,b)\) y que \(c\in I\) es un punto crítico (es decir, \(f'(c)=0\)). Entonces, pueden darse las siguientes situaciones (estudio del signo de la derivada en los intervalos \((a,c)\) y \((c,b)\)):
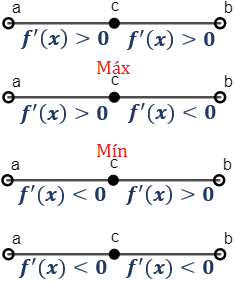
Es decir, \(c\) es un máximo si la función es \(f\) es creciente a su izquierda y decreciente a su derecha. Y es un mínimo si \(f\) es decreciente a su izquierda y creciente a su derecha.
Para saber si \(f'\) es positiva o negativa un intervalo, sólo tenemos que ver el signo de \(f'(x)\) de cualquier \(x\) de dicho intervalo.
Ejemplo
Vamos a calcular los extremos de la función
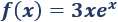
La primera derivada es
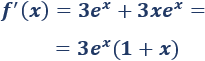
Igualamos a \(0\) y resolvemos la ecuación para hallar los puntos críticos:
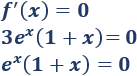
La función \(e^x\) nunca es igual a \(0\). Por tanto, el único punto crítico es \(x = -1\).
El punto crítico divide los reales en dos intervalos:

Evaluamos la derivada \(f'\) en un punto arbitrario de cada uno de los intervalos para saber si \(f\) es creciente o decreciente:
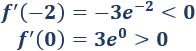
Por tanto, \(f\) es monótona decreciente en el intervalo \((-\infty,-1)\) y monótona creciente en \((-1,+\infty)\).
Como consecuencia, \(x = -1\) es un mínimo. Además, por la monotonía de la función, se deduce que es un mínimo absoluto.
Gráfica:
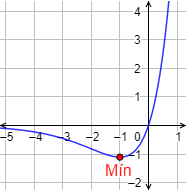
3. Regla de la segunda derivada
La regla de la segunda derivada permite determinar si un punto crítico es un mínimo o un máximo relativo según el signo de la segunda derivada.
Regla de la segunda derivada:
Si \(f\) es dos veces derivable y \(x=c\) es un punto crítico, entonces
-
\(c\) es un mínimo relativo si \(f''(c)> 0\)
-
\(c\) es un máximo relativo si \(f''(c)< 0\)
-
Si \(f''(c) = 0\), la regla no determina si se trata o no de un extremo.
Demostración en Criterio de la segunda derivada.
Ejemplo
La segunda derivada de la función del ejemplo anterior, \(f(x) = 3xe^x\), es

Evaluamos el punto crítico \(x = -1\):
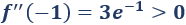
Por tanto, se trata de un mínimo.
4. Problemas resueltos
Nota: no aplicamos la regla de la segunda derivada ya que nos bastamos con la primera.
Problema 1
Determinar la monotonía y los extremos de la función
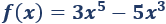
Solución:
Calculamos la primera derivada:
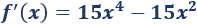
Igualamos la derivada a \(0\) y resolvemos la ecuación:
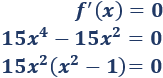
Las soluciones son \(x=0\), \(x=1\) y \(x=-1\). Tenemos \(3\) puntos críticos que dividen los reales en \(4\) intervalos:
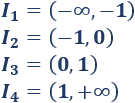
Evaluamos la derivada en un punto de cada intervalo para determinar su signo:
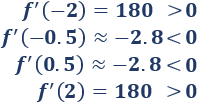
Por tanto, la función \(f\) es monótona creciente en los intervalos \(I_1\) e \(I_4\) y monótona decreciente en los intervalos \(I_2\) e \(I_3\).
La función tiene un máximo en \(x=-1\) y un mínimo en \(x=1\).
Nota: puede ayudar representar los intervalos y la monotonía de la función:
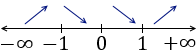
Tomando límites cuando \(x\to \pm \infty\), deducimos que los extremos no son absolutos.
Gráfica:
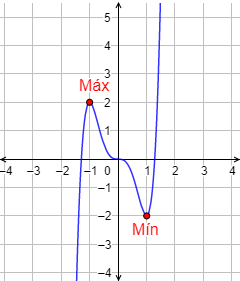
Problema 2
Determinar los extremos de la función
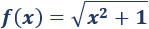
Solución:
Derivamos la función:
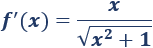
El único punto crítico es \(x = 0\).
Como el radicando (y la raíz) siempre es positiva, fácilmente vemos que la derivada es negativa en los reales negativos y positiva en los positivos. Luego \(f\) es decreciente en los negativos y creciente en los positivos.
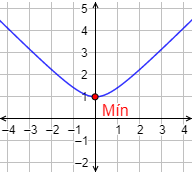
Como consecuencia, \(x=0\) es un mínimo absoluto.
Gráfica:
Problema 3
Determinar la monotonía y los extremos de la función
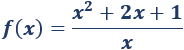
Solución:
Es más rápido calcular la derivada si reescribimos la función:
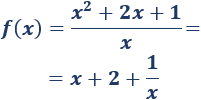
La derivada es
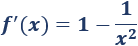
Calculamos los puntos críticos:
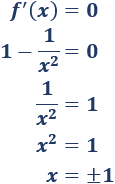
Los puntos críticos son \(x=-1\) y \(x=1\).
Observad que la función no está definida en \(x=0\), así que tenemos que estudiar el signo de la derivada en \(4\) intervalos:
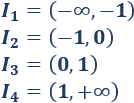
Evaluamos la derivada en un punto de cada intervalo para determinar su signo:
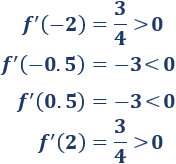
Por tanto, la función \(f\) es monótona creciente en los intervalos \(I_1\) e \(I_4\) y monótona decreciente en los intervalos \(I_2\) e \(I_3\).
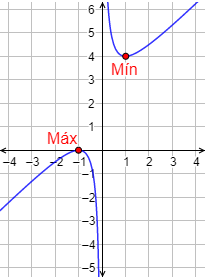
Hay un máximo en \(x=-1\) y un mínimo en \(x=1\).
Tomando límites, deducimos que no son extremos absolutos.
Gráfica:
Problema 4
Determinar los extremos de la función
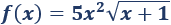
Solución:
Antes que nada, hay que tener en cuenta que el dominio de esta función son los reales mayores o iguales que \(-1\), puesto que el radicando debe ser no negativo.
Calculamos la derivada:
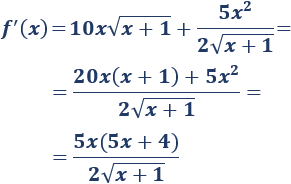
Calculamos los puntos críticos:
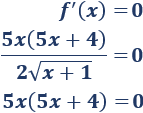
Por tanto, tenemos los puntos críticos \(x = 0\) y \(x = -4/5\).
Tenemos los siguientes intervalos:
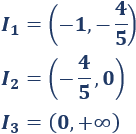
Estudiamos el signo de la derivada en cada intervalo:
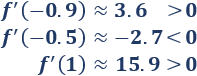
Teniendo en cuenta la monotonía, \(x=-4/5\) es un máximo y \(x =0\) es un mínimo.
Además, el extremo del intervalo \(-1\) es un mínimo.
El máximo no es absoluto puesto que la función crece cuando \(x\) tiende a \(+\infty\).
Uno o dos de los mínimos podría ser absoluto. Comparamos sus imágenes:
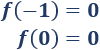
Ambos mínimos son absolutos.
Gráfica:
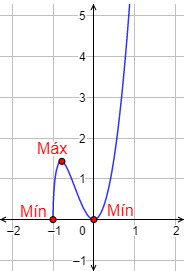
Problema 5
Calcular los extremos de la siguiente función definida a trozos:
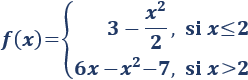
Solución:
Calculamos la derivada:
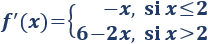
Los puntos críticos son \(x=0\) y \(x = 3\). Además, hay que añadir \(x = 2\), que es donde cambia la definición de la función.
Tenemos los intervalos
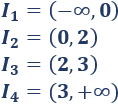
Estudiamos el signo de la derivada en los intervalos:
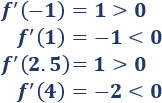
Por tanto, tenemos
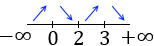
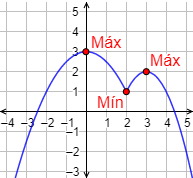
Hay un máximo en \(x = 0\) y otro en \(x=3\) y un mínimo en \(x = 2\).
Teniendo en cuenta los límites cuando \(x\to\pm \infty\), uno o los dos máximos pueden ser extremos absolutos. El mínimo no es absoluto.
Evaluamos la función en los máximos:
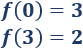
Por tanto, \(x = 0\) es un máximo absoluto.
Gráfica:
Más problemas similares: Problemas de monotonía de funciones.