Problemas de optimización
Resolvemos problemas de optimizar funciones mediante cálculo diferencial básico (regla de la primera derivada). Lo más importante es plantear la función que hay que optimizar.
Índice:
- Introducción y ejemplo
- Problemas resueltos
1. Introducción y ejemplo
El criterio de la primera derivada proporciona la monotonía de una función \(f\) derivable en un intervalo \(I=(a,b)\):
- \(f\) es creciente en \(I\) si \(f'(x)>0\) para todo \(x\in I\)
- \(f\) es decreciente en \(I\) si \(f'(x)<0\) para todo \(x\in I\)
Como consecuencia, los puntos que anulan la primera derivada (llamados puntos críticos) son candidatos a ser extremos relativos.
Por tanto, para resolver los problemas tenemos que
- Platear la función \(f(x)\)
- Calcular la derivada \(f'(x)\)
- Calcular los puntos críticos (soluciones de \(f'(x)=0\))
- Determinar si los puntos críticos son máximos o mínimos a partir de la monotonía
También, se puede aplicar el criterio de la segunda derivada para el paso \(4\).
Ejemplo
El coste de fabricación de una bolsa hermética de plástico viene dado por la función
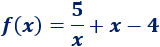
siendo \(x>0\) el volumen de la bolsa (en litros).
¿Cuál debe ser el volumen de la bolsa para que su coste sea mínimo? ¿Cuál es dicho coste?
Derivamos la función:
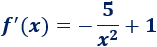
Igualamos la derivada a \(0\) y resolvemos:
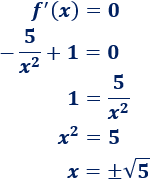
El único punto crítico que tenemos es \(x=\sqrt{5}\) (descartamos el negativo porque \(x\) debe ser positiva).
El signo de la derivada se mantiene constante en los intervalos
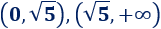
Evaluamos la derivada en cualquier punto de cada intervalo:
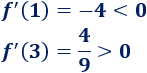
Por tanto, la función es decreciente el primer intervalo y creciente en el segundo. Esto implica que el punto crítico es un mínimo de la función.
El volumen debe ser \(\sqrt{5}\) litros para que el coste sea mínimo.
Calculamos el coste:
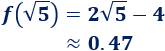
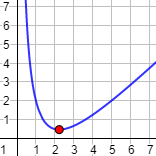
Gráfica de la función (para \(x>0\)):
2. Problemas resueltos
Problema 1
Disponemos de una barra de aluminio de \(6\) metros para construir una portería de fútbol. Si queremos que el área de la portería sea máxima, ¿cuánto deben medir los postes y el larguero?
Solución:
Sean \(x\) la longitud del larguero e \(y\) la de los postes:
La suma de las tres barras debe ser \(6\):
De donde podemos obtener \(y\) en función de \(x\):
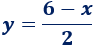
El área de la portería es
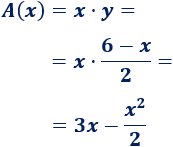
Derivamos la función:
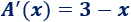
El único punto crítico es \(x=3\).
La derivada es positiva para \(x<3\) y negativa para \(x>3\). Por tanto, \(x=3\) es un máximo de la función área.
Calculamos la longitud de los postes:
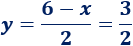
Por tanto, el larguero debe medir \(3\) metros y los postes, \(1.5\) metros.
Gráfica de la función:
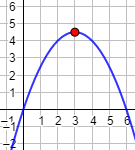
Problema 2
Hallar dos números \(x,y\in ]0,5[\) cuya suma sea \(5\) de modo que la diferencia \(x-1/y\) sea máxima.
Solución:
Como suman \(5\),
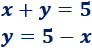
La función a maximizar es
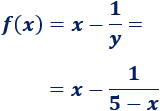
Calculamos la derivada:
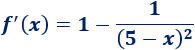
Operamos en la derivada:
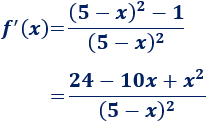
La derivada se anula cuando el numerador es \(0\). Por tanto, tenemos que resolver una ecuación de segundo grado:
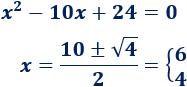
Tenemos dos puntos críticos, pero nos interesa el que es menor que \(5\).
Estudiamos la monotonía en los siguientes intervalos (no olvidéis que \(x\) debe ser menor que \(5\)):
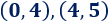
Evaluamos la derivada en un punto de cada intervalo:
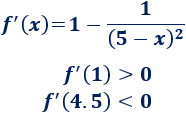
Atendiendo a la monotonía de la función, deducimos que hay un máximo en \(x = 4\).
Calculamos \(y\):
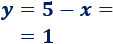
Por tanto, son los números \(4\) y \(1\).
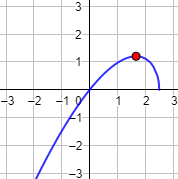
Gráfica de la función:
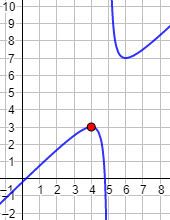
Problema 3
Calcular la longitud de los lados del triángulo isósceles cuyo perímetro es \(5\) para que su área sea máxima.
Solución:
Sea \(h\) la altura, \(x\) la base e \(y\) cada uno de los dos lados del triángulo:
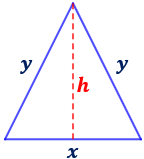
El perímetro es
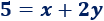
De donde podemos obtener \(y\) en función de \(x\):
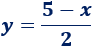
El área del triángulo es
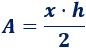
Tenemos que escribir \(h\) en función de \(x\).
Aplicamos Pitágoras:
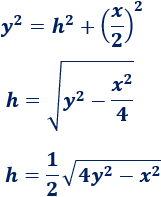
Escribimos \(y\) en función de \(x\):
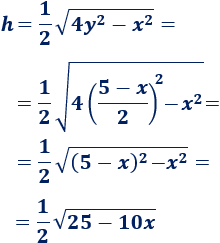
Por tanto, el área del triángulo en función de \(x\) es
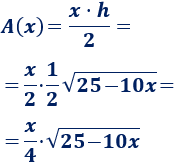
El radicando debe ser positivo:
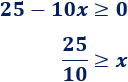
Además, \(x\) debe ser positiva (por ser una longitud).
Derivamos la función:
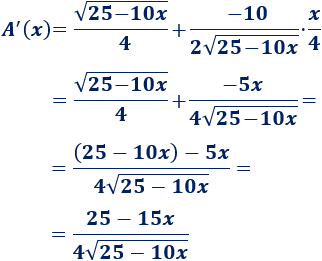
Calculamos el único punto crítico:
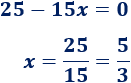
Estudiamos el signo de la derivada (depende del signo del numerador):
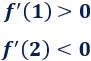
La función es creciente en \((0,5/3)\) y decreciente en \((5/3, 25/10)\). Por tanto, \(x = 5/3\) es un máximo.
Calculamos los otros lados:
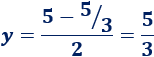
Los tres lados deben medir \(5/3\), por lo que se trata de un triángulo equilátero.
Gráfica de la función:
Problema 4
Se quiere construir un marco rectangular para un cuadro de área \(8dm^2\). El precio del marco lateral es de \(4€/dm\) y el del marco superior e inferior es de \(2€/dm\).
Calcular las dimensiones del marco para que su coste sea mínimo. ¿Cuál es el coste?
Solución:
Si \(x\) es la base e \(y\) es la altura, el área del cuadro es
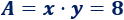
El coste del marco es
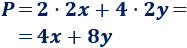
Podemos escribir \(y\) en función de \(x\) despejando en la ecuación del área:
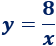
Así, podemos escribir el coste en función de \(x\):
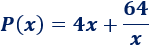
Tenemos que minimizar esta función.
Calculamos la derivada:
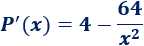
Calculamos los puntos críticos igualando la derivada a \(0\):
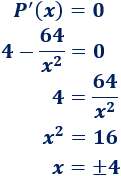
Como \(x\) debe ser positivo, descartamos la solución \(x = -4\).
Estudiamos el signo de la derivada en los dos intervalos:
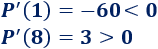
Por la regla de la primera derivada, la función es decreciente en el intervalo \((0,4)\) y creciente en el intervalo \((4,+\infty)\). Por tanto, hay un mínimo en \(x = 4\).
Luego la base del marco debe medir \(4dm\) y el lateral debe medir \(2dm\).
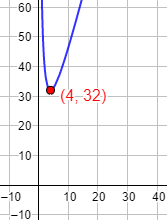
Gráfica de la función:
Problema 5
Se quiere construir una caja sin tapa a partir de una hoja de cartón de \(16\times 8cm\). Para ello, se corta un cuadrado de lado \(L\) en cada esquina y se dobla la hoja levantando los cuatro laterales de la caja.
Determinar el lado \(L\) de la caja para que su volumen sea máximo bajo la condición de que \(L\) sea \(1\leq L\leq 4\). ¿Cuál será el volumen de la caja?
Solución:
Al cortar las cuatro esquinas de lado \(L\), dos de los lados miden \(16-2L\) y los otros dos miden \(8-2L\):
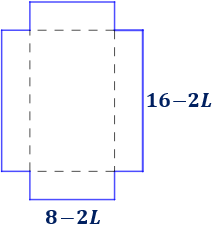
El volumen de la caja es
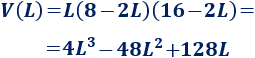
Derivamos la función:
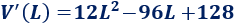
Calculamos los puntos críticos:
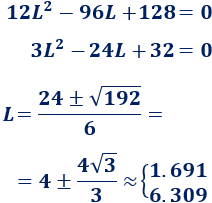
Como \(L\) debe ser \(1\leq L\leq 4\), tenemos que estudiar la monotonía en los intervalos
Es decir, descartamos el segundo punto crítico.
Estudiamos el signo de la derivada:
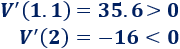
Por tanto, el punto crítico es un máximo.
El lado \(L\) debe medir
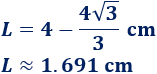
El volumen de la caja es
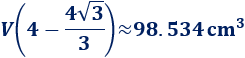
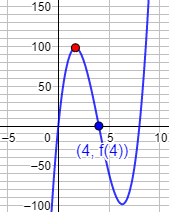
Gráfica de la función:
Más problemas similares: Problemas de optimizar.