Función definida a trozos
Explicamos el concepto de función definida a trozos, proporcionamos ejemplos (con gráficas) y su continuidad. También, resolvemos algunos problemas.
Índice:
- Concepto y ejemplos
- Continuidad
- Problemas resueltos
1. Concepto y ejemplos
Una función definida a trozos es una función cuya definición cambia según el valor que toma la variable. También, recibe el nombre de función definida por partes, función segmentada y función seccionada, entre otros.
Ejemplo
Sea la función
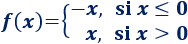
Para calcular la imagen de un punto \(x\), usamos la primera definición si \(x\leq 0\) y la segunda si \(x> 0\).
Por ejemplo,
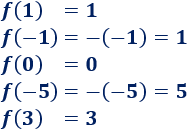
Esta función es la función valor absoluto \(f(x) = |x|\).
También, podemos usar intervalos en lugar de desigualdades:
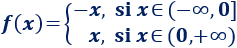
La gráfica de la función es
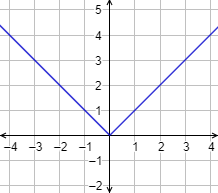
Observad que la parte de gráfica donde \(x\leq 0\) coincide con la gráfica de la función \(y=-x\) y la parte donde \(x> 0\) coincide con la de \(y=x\).
Ejemplo
La siguiente función está compuesta por una función lineal y una cuadrática:
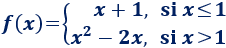
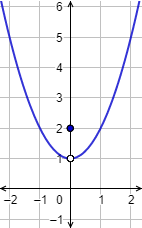
Gráfica:
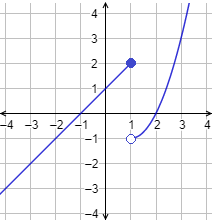
Utilizamos el punto sólido y el punto vacío para enfatizar que la imagen de \(1\) es \(2\) y no \(-1\), puesto que hay que utilizar la primera definición de la función.
Ejemplo
Un ejemplo típico e importante de función por partes es la llamada función de Dirichlet:
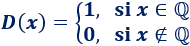
Es decir, la imagen de los racionales es \(1\) y la de los irracionales es \(0\).
2. Continuidad
La continuidad de una función definida a trozos depende de la continuidad de las partes que la conforman y, además, los puntos donde cambia la definición son posibles puntos de discontinuidad.
Si \(x=a\) es un punto donde cambia la definición, la función es continua en dicho punto si existen los límites laterales y son iguales a la imagen de \(x=a\), es decir,
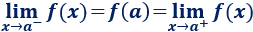
Ejemplo
La función de un ejemplo anterior
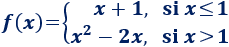
es discontinua en el punto \(x=1\) puesto que los límites laterales no coinciden:
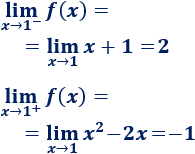
En los otros puntos, la función es continua.
Ejemplo
En la función valor absoluto, la definición cambia cuando \(x=0\), pero los límites laterales son iguales a \(f(0)=0\).
Ejemplo
¡La función de Dirichlet no es continua en ningún punto!
3. Problemas resueltos
Problema 1
Determinar los intervalos de definición de la siguiente función a partir de su gráfica:
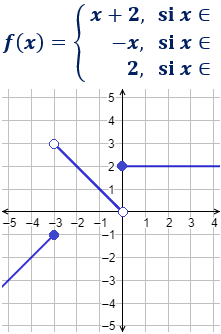
¿Es una función continua?
Solución:
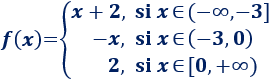
La función es continua excepto en los puntos \(x=-3\) y \(x=0\), puntos donde los límites laterales no coinciden.
Problema 2
Hallar el valor del parámetro \(a\) para que la siguiente función sea continua:
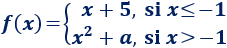
Solución:
En los puntos \(x\neq -1\), la función es continua para cualquier valor de \(a\) puesto que es una función lineal y una función cuadrática.
Para evitar la discontinuidad en \(x=-1\), los límites laterales deben coincidir con \(f(-1) = 4\):
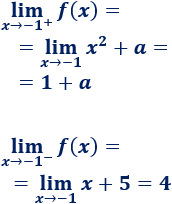
Resolvemos la ecuación que obtenemos al igualar los resultados:
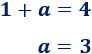
Por tanto, la función es continua para el valor \(a=3\).
Gráfica:
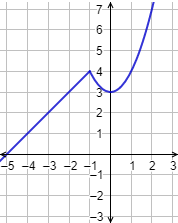
Problema 3
Hallar los parámetros \(a\) y \(b\) para que la siguiente función sea continua:
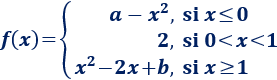
Solución:
Tomando límites cuando \(x\) tiende a \(0\), tenemos
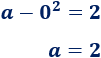
Tomando límites cuando \(x\) tiende a \(1\), tenemos
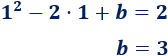
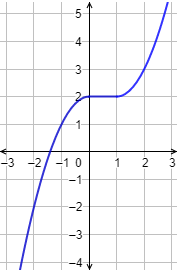
Gráfica de la función:
Problema 4
Representar la gráfica y calcular los puntos de discontinuidad de la función
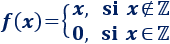
Recordad que \(\mathbb{Z} = \{0,1,-1,2,-2,...\}\).
Solución:
Representamos la gráfica:
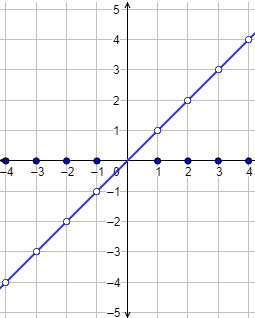
La función es discontinua en los enteros excepto en \(0\).
Problema 5
Determinar y justificar la continuidad de la función
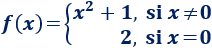
Solución:
La función \(x^2+1\) es continua, así que \(f\) es continua cuando \(x\neq 0\).
En el punto \(x= 0\), los límites laterales coinciden:
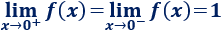
Pero la función es discontinua en \(x =0\) porque que los límites laterales no son iguales a \(f(0) = 2\).
Gráfica:
Más problemas similares: Funciones definidas a trozos.