Puntos equidistantes
Explicamos el concepto de punto equidistante, con ejemplos y problemas resueltos.
Índice:
- Definición
- Ejemplos
- Problemas resueltos
1. Definición
Un punto \(P\) es equidistante de un conjunto de puntos \(x_1\), \(x_2\), …, \(x_n\) si la distancia de \(P\) a cada uno de estos puntos \(x_i\) es la misma:
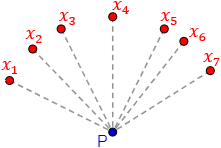
Observad que el punto azul equidista de los puntos rojos, pero los puntos rojos no son equidistantes entre ellos.
2. Ejemplos
Ejemplo 1
El punto \(P=(1,0)\) es equidistante a los puntos \(x_1=(1,1)\) y \(x_2 = (2,0)\):
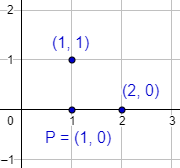
La distancia de \(P\) a los puntos \(x_1\) y \(x_2\) es \(1\).
Ejemplo 2
Los extremos de un segmento equidistan del punto medio del mismo:
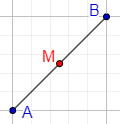
Ejemplo 3
Una circunferencia de radio \(r\) y centro \(P\) es un conjunto de puntos equidistantes de \(P\):
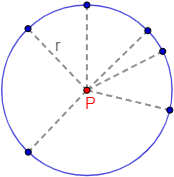
La distancia de todos los puntos de la circunferencia a su centro es igual al radio, \(r\).
Ejemplo 4
En un cuadrado, los vértices equidistan del centro:
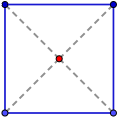
Observad que los vértices no son equidistantes entre sí.
Ejemplo 5
En un triángulo equilátero, los vértices son equidistantes entre sí:
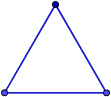
También, los vértices equidistan del ortocentro:
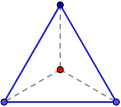
Y además, los puntos medios de cada lado equidistan del ortocentro:
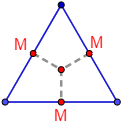
Nota: el ortocentro es el punto donde intersectan las tres alturas del triángulo.
Ejemplo 6
En un triángulo cualquiera, los tres vértices equidistan del centro de la circunferencia circunscrita:
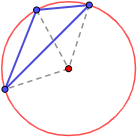
Observad que los vértices están sobre una circunferencia y, por tanto, equidistan de su centro.
3. Problemas resueltos
Problema 1
Determinar si los siguientes tres puntos son equidistantes entre sí. ¿Qué figura forman si los unimos?
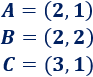
Solución:
Vamos a calcular la distancia entre los puntos.
Recordamos la fórmula para calcular la distancia entre los puntos \((a,b)\) y \((x,y)\):
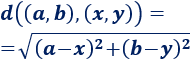
Distancia entre \(A\) y \(B\):
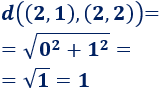
Distancia entre \(A\) y \(C\):
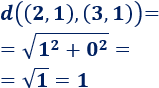
Distancia entre \(B\) y \(C\):
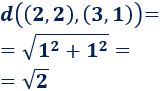
Los tres puntos no son equidistantes entre sí, pero el punto \(A\) sí equidista de los puntos \(B\) y \(C\).
Representación:
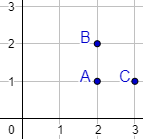
La unión de los puntos es un triángulo rectángulo.
Problema 2
Hallar un punto que sea equidistante a los siguientes puntos:
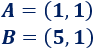
Solución:
Observad que la segunda coordenada de los puntos es la misma, con lo que los puntos están alineados en una línea horizontal. Esto facilita calcular un punto equidistante, por ejemplo, el punto medio, \(C=(3,1)\):
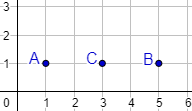
Otra posibilidad es construir un triángulo isósceles o equilátero.
Triángulo isósceles:
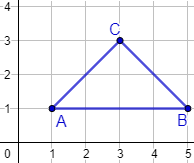
En este ejemplo, se trata del punto
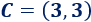
Triángulo equilátero:
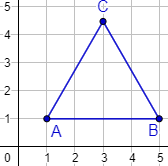
En este ejemplo, se trata del punto
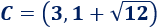
Nota: en el caso del triángulo isósceles, el punto \(C\) es equidistante a los otros dos puntos. En el caso del triángulo equilátero, los tres puntos son equidistantes entre sí.
Problema 3
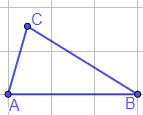
¿Qué par de vértices del siguiente triángulo equidistan del otro vértice?
Solución:
Los vértices \(A\) y \(C\) equidistan del vértice \(B\).
Problema 4
¿A qué punto son equidistantes los puntos \((x,y)\) que cumplen la siguiente ecuación?
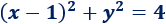
Solución:
Se trata de la ecuación de la circunferencia de radio \(r=2\) y de centro \(P = (1,0)\).
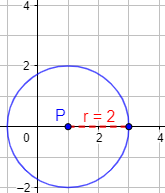
Los puntos que cumplen la ecuación son equidistantes del centro, pues precisamente ésta es la definición de una circunferencia.
Problema 5
¿Los puntos que conforman una elipse equidistan de sus focos?
Solución:
No, y es fácil de ver:
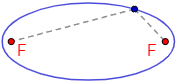
Una elipse es el conjunto de puntos tales que la suma de las distancias a los focos es igual a una constante.
Más problemas similares: