Recta que une dos puntos
Explicamos cómo calcular la recta que une por dos puntos del plano real \(\mathbb{R}^2\).
Índice:
- Método
- Ejemplo
- Puntos alineados
- Problemas resueltos
1. Método
La ecuación de una recta del plano es

- el coeficiente \(m\) es la pendiente de la recta
- y \(n\) es la ordenada en el origen.
Cuando un punto \(A=(a_1,a_2)\) pertenece a una recta, sus coordenadas deben cumplir la ecuación de la recta. Es decir, se cumple que

Por tanto, dados dos puntos, podemos calcular la recta que los une a partir de sus coordenadas: sólo tenemos que sustituir las coordenadas de los puntos en la ecuación y resolver el sistema de ecuaciones lineales obtenido.
2. Ejemplo
Vamos a calcular la recta que une los puntos \(A = (2,1)\) y \(B=(3,3)\).
Sustituimos las coordenadas de \(A=(2,1)\) en la ecuación de la recta:

Sustituimos las coordenadas de \(B=(3,3)\) en la ecuación de la recta:

Tenemos un sistema de dos ecuaciones con dos incógnitas:
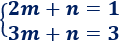
Recordad que tenemos varios métodos para resolver un sistema: sustitución, igualación y reducción (entre otros).
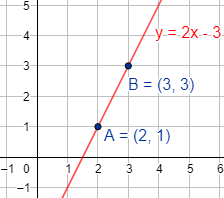
La solución del sistema es \(m = 2\) y \(n = -3\), así que la ecuación de la recta que une los puntos \(A\) y \(B\) es

Representación:
3. Puntos alineados
Tres (o más) puntos están alineados si todos ellos pertenecen a una misma recta.
Ejemplo
Los puntos \(A=(1,1)\), \(B=(2,2)\) y \(C=(3,3)\) están alineados porque pertenecen a la recta \(y = x\):
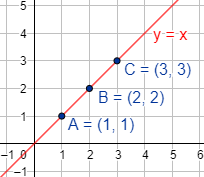
Observad que los tres puntos cumplen la ecuación \(y=x\).
En cambio, los puntos \(A=(1,1)\), \(B=(2,2)\) y \(C=(1,4)\) no están alineados:
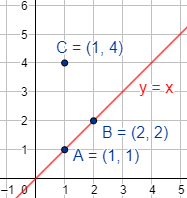
Observad que el punto \(C\) no cumple la ecuación \(y=x\).
4. Problemas resueltos
Problema 1
Hallar la recta que une los puntos \(A = (2,-1)\) y \(B=(-1,8)\).
Solución:
La ecuación de una recta es

Sustituimos las coordenadas del punto \(A=(2,-1)\) en la ecuación de la recta:
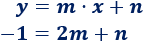
Sustituimos las coordenadas de \(B=(-1,8)\) en la ecuación de la recta:
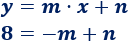
Tenemos un sistema de ecuaciones:
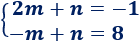
La solución del sistema es
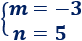
Por tanto, es la recta
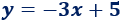
Representación:
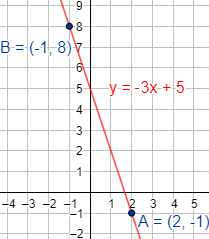
Problema 2
Hallar la recta con pendiente \(3\) que pase por el punto \(A = (1,-1)\).
Solución:
La ecuación de una recta es

Como su pendiente debe ser \(3\), la recta que buscamos es

Tenemos que calcular la ordenada, \(n\).
Sustituimos las coordenadas del punto \(A=(1,-1)\) para hallar \(n\):
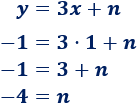
Por tanto, se trata de la recta

Representación:

Problema 3
Determinar si los puntos \(A = (1,1)\), \(B=(3,-3)\) y \(C=(-2,7)\) están alineados.
Solución:
Calculamos la recta que une los puntos \(A = (1,1)\) y \(B=(3,-3)\) sustituyendo sus coordenadas:
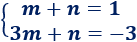
La solución del sistema es
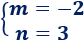
Es la recta \(y = 3-2x\).
Comprobamos si el punto \(C=(-2,7)\) también está en dicha recta:
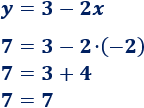
El punto \(C\) verifica la ecuación de la recta. Por tanto, los tres puntos están alineados.
Representación:
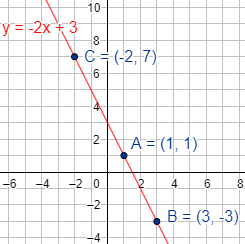
Problema 4
Determinar si los puntos \(A = (0,1)\), \(B=(1,0)\) y \(C=(10,-8)\) están alineados.
Solución:
Calculamos la recta que une los puntos \(A = (0,1)\) y \(B=(1,0)\) sustituyendo sus coordenadas:
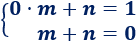
La solución del sistema es
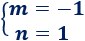
Es la recta \(y = 1-x\).
Comprobamos si el punto \(C=(10,-8)\) también está en dicha recta:
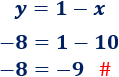
El punto \(C\) no verifica la recta (porque obtenemos una igualdad falsa), así que los tres puntos no están alineados.
Representación:

Más problemas similares: rectas y parábolas.