Problemas de trigonometría básica:
Seno, coseno y tangente
En esta página definimos las razones trigonométricas seno, coseno y tangente de un ángulo como la razón entre los lados de un triángulo rectángulo. También, resolvemos 10 problemas de aplicación.
Introducción
Consideremos un triángulo rectángulo (con un ángulo recto) y un ángulo \(\alpha\):
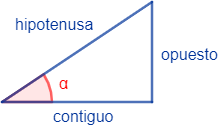
El lado opuesto al ángulo recto (el de 90º) se denomina hipotenusa y los otros dos lados son los catetos:
-
el cateto opuesto es el que está enfrente del ángulo \(\alpha\)
-
y el cateto contiguo o adyacente es el otro cateto, es decir, el que está en contacto con el ángulo \(\alpha\).
Las razones trigonométricas se definen como la razón entre los lados del triángulo:
Seno
El seno de \(\alpha\) es el cateto opuesto entre la hipotenusa:
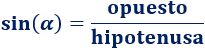
Coseno
El coseno de \(\alpha\) es el cateto contiguo o adyacente entre la hipotenusa:
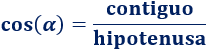
Tangente
La tangente de \(\alpha\) es seno entre el coseno, es decir, el cateto opuesto entre el contiguo:
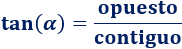
Otra forma de escribir la tangente de \(\alpha\) es \(tg(\alpha)\).
Nota: tened en cuenta que, si cambiamos de ángulo, entonces cambian los catetos: el opuesto pasa a ser el contiguo y viceversa.
Una regla mnemotécnica que puede ayudaros a recordar las fórmulas:
- Seno - opuesto
- Coseno - contiguo
- Tangente = seno/coseno = opuesto/contiguo
Finalmente, veamos por encima qué son las razones trigonométricas inversas:
Razones inversas
Si conocemos el seno, el coseno o la tangente del ángulo \(\alpha\) y queremos calcular el ángulo \(\alpha\), usamos las razones trigonométricas inversas:
-
La inversa del seno es el arcoseno, escrita como \(arcsin\):
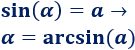
En la calculadora es la tecla \(sin^{-1}\).
-
La inversa del coseno es el arcocoseno, escrita como \(arccos\):
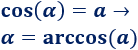
En la calculadora es la tecla \(cos^{-1}\).
-
La inversa de la tangente es la arcotangente, escrita como \(arctan\):
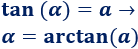
En la calculadora es la tecla \(tan^{-1}\).
Problemas resueltos de trigonometría
Problema 1
Determinar si los lados \(a\), \(b\) y \(c\) de cada uno de los siguientes triángulos rectángulos son la hipotenusa, el lado opuesto o el lado contiguo al ángulo \(\alpha\) representado:
Triángulo 1:
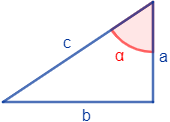
Solución:
- \(a\) es el lado contiguo o adyacente
- \(b\) es el lado opuesto
- \(c\) es la hipotenusa
Triángulo 2:
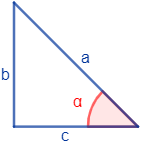
Solución:
- \(a\) es la hipotenusa
- \(b\) es el lado opuesto
- \(c\) es el lado contiguo o adyacente
Triángulo 3:
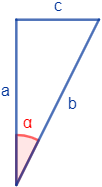
Solución:
- \(a\) es el lado contiguo o adyacente
- \(b\) es la hipotenusa
- \(c\) es el lado opuesto
Problema 2
(Con calculadora) Calcular los ángulos \(\alpha\) sabiendo cuánto valen su seno o su coseno:
a) \(sin(\alpha ) = 0.999390827\)
b) \(sin(\alpha ) = 0.6691306064\)
c) \(sin(\alpha ) = 0.7660444431\)
d) \(sin(\alpha ) = 0.9743700648\)
e) \(cos(\alpha ) = 0.8090169944\)
f) \(cos(\alpha ) = 0.2588190451\)
g) \(cos(\alpha ) = 0.9271838546\)
h) \(cos(\alpha ) = 0.4067366431\)
Problema 3
Simplificar las siguientes expresiones:
-
\( sin(x) - 2(sin(x)-3sin(2x))\)
-
\(2·(cos(x)-cos(2x))-(2cos(x)-cos(2x))\)
-
\(2sin(x)-\frac{ 4sin(x)-cos(x)}{2}\)
Resolvemos:
Tenemos que simplificar las ecuaciones del mismo modo que hacemos con las expresiones algebraicas con \(x\): podemos sumar o restar \(sin(x)\) con \(sin(x)\), pero no podemos sumar, por ejemplo, los senos con los cosenos ni \(sin(x)\) con \(sin(2x)\).
-
\( sin(x) - 2(sin(x)-3sin(2x))\)
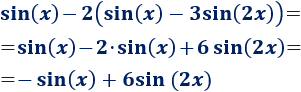
-
\(2·(cos(x)-cos(2x))-(2cos(x)-cos(2x))\)
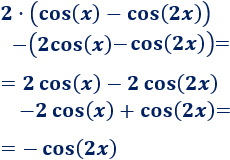
-
\(2sin(x)-\frac{ 4sin(x)-cos(x)}{2}\)
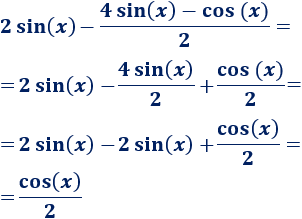
Problema 4
Calcular el valor de \(x\) de cada figura utilizando las razones trigonométricas viastas:
Figura 1:
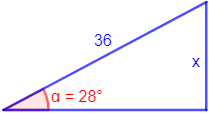
Resolvemos:
Conocemos la hipotenusa y el ángulo. Como queremos calcular el lado opuesto, utilizamos el seno:
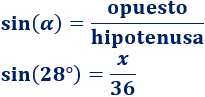
Despejamos la incógnita:
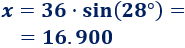
El lado mide, aproximadamente, 16.900.
Figura 2:
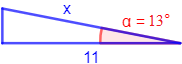
Resolvemos:
En esta figura conocemos el lado contiguo y el ángulo. Para calcular la hipotenusa, utilizamos el coseno:
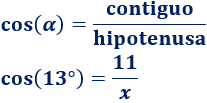
Despejamos la incógnita:
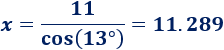
La hipotenusa mide, aproximadamente, 11.289.
Figura 3:
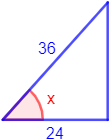
Resolvemos:
Conocemos el lado contiguo y la hipotenusa, así que utilizamos el coseno:
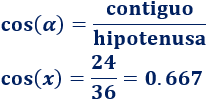
Despejamos la incógnita:
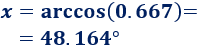
Por tanto, el ángulo mide, aproximadamente, 48.164°.
Figura 4:
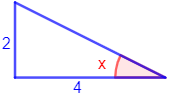
Resolvemos:
Como conocemos el lado opuesto y el contiguo al ángulo, utilizamos la tangente:
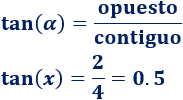
Despejamos la incógnita:

Por tanto, el ángulo mide, aproximadamente, 26.565°.
Problema 5
Calcular el ángulo \(\alpha\) de cada uno de los siguientes triángulos (tendremos que usar las inversas del seno, coseno o tangente según los datos que tengamos):
Triángulo 1:
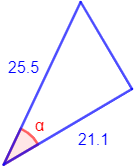
Resolvemos:
Como conocemos el lado contiguo y la hipotenusa, usamos el coseno:

Despejamos la incógnita:
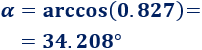
Por tanto, el ángulo mide, aproximadamente, 34.208°.
Triángulo 2:
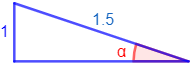
Resolvemos:
Como conocemos el lado opuesto y la hipotenusa, usamos el seno:
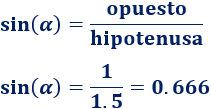
Despejamos la incógnita:

Por tanto, el ángulo mide, aproximadamente, 41.836°.
Triángulo 3:
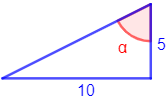
Resolvemos:
Como conocemos el lado contiguo y el opuesto, usamos la tangente:
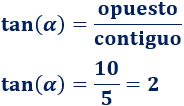
Despejamos la incógnita:

Por tanto, el ángulo mide, aproximadamente, 63.435°.
Problema 6
Calcular la base (lado \(x\)) del siguiente triángulo escaleno:
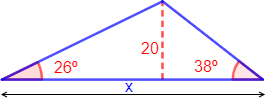
Resolvemos:
La altura (segmento discontinuo) divide el triángulo en dos triángulos rectángulos.
El lado \(x\) es la suma de las bases de los dos triángulos:
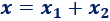
Y la altura (segmento discontinuo) coincide con el lado opuesto a los ángulos representados.
Por tanto, utilizando la tangente, podemos hallar las bases.
Calculamos la base del triángulo del lado izquierdo:
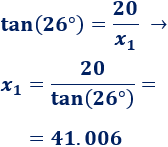
Calculamos la base del otro:
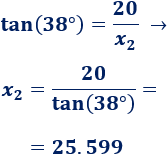
La base del triángulo del problema mide, aproximadamente,
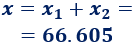
Problema 7
Desde un supermercado se observa el ático de un rascacielos de 527 metros de altura bajo un ángulo de 42°. Calcular la distancia que hay desde el supermercado hasta la puerta del rascacielos.
Resolvemos:
La representación del problema es
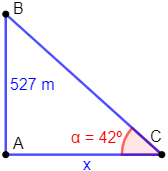
donde
- C es el supermercado
- B es el ático del edificio
- A es la base del edificio donde se halla la puerta del mismo
- x es la distancia a calcular
La distantica \(x\) es el cateto contiguo al ángulo \(\alpha\).
Como conocemos el ángulo y su lado opuesto, usamos la tangente:
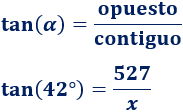
Despejamos la incógnita:
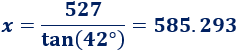
Por tanto, la distancia del supermercado al rascacielos es de, aproximadamente, 585.293 metros.
Problema 8
Calcular el perímetro del siguiente polígono:
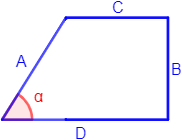
donde
- \( \alpha = 58^\circ \)
- \( B = C\)
- \( A = 24.6m\)
Resolvemos:
En el lado izquierdo hay un triángulo, representamos su altura:
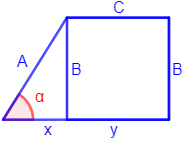
Observad que la altura del triángulo mide lo mismo que lado \(B\) de la figura. También, hemos divido la base de la figura en dos segmentos: \(x\) e \(y\).
Como conocemos el lado \(A\) y el ángulo \(\alpha\), podemos calcular \(B\) con el seno:
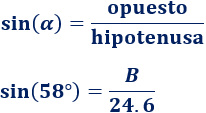
Por tanto, el lado \(B\) (y también los lados \(C\) e \(y\)) mide
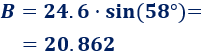
Ahora, calculamos la base del triángulo con el coseno:
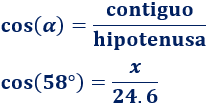
El lado \(x\) mide
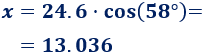
Calculamos el perímetro de la figura:
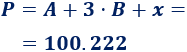
El perímetro es, aproximadamente, 100.222 metros.
Problema 9
Ramiro está volando su cometa y le gustaría saber qué altura alcanza. La sombra de la sombra de la cometa comienza a sus pies y termina a 6.7 metros y el ángulo que forma el cable con el suelo es de 39°. ¿A qué altura se encuentra la cometa?
Resolvemos:
La situación es la siguiente:
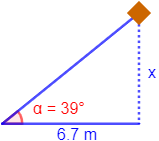
Utilizamos la tangente:
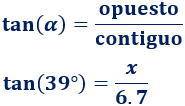
Por tanto, la altura a la que se encuentra la cometa es, aproximadamente, 5.426 metros:
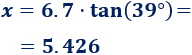
Problema 10
Calcular la base (lado \(x\)) de la siguiente figura construida con dos triángulos rectángulos:
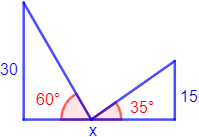
Resolvemos:
Dividimos la base de la figura en la base de los dos triángulos:
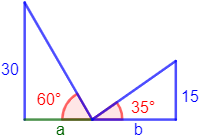
Podemos calcular \(a\) y \(b\) con la tangente de ambos ángulos:
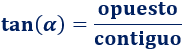
Calculamos \(a\):
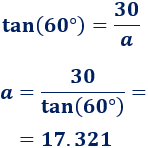
Calculamos \(b\):
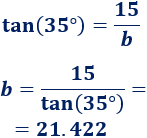
Calculamos \(x\):
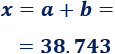
Por tanto, la base de la figura mide, aproximadamente, 38.743.
Más información y problemas resueltos de trigonometría y geometría:







