Distancia entre puntos
Explicamos cómo calcular la distancia euclídea (o euclidiana) entre dos puntos de la recta, del plano y del espacio reales, es decir, \(\mathbb{R}\), \(\mathbb{R}^2\) y \(\mathbb{R}^3\). También, resolvemos algunos problemas.
Índice:
- Distancia en \(\mathbb{R}\)
- Distancia en \(\mathbb{R}^2\)
- Distancia en \(\mathbb{R}^3\)
1. Distancia en \(\mathbb{R}\)
Sean \(x\) e \(y\) dos puntos de \(\mathbb{R}\), la distancia de \(x\) a \(y\) se define como el valor absoluto de su diferencia:
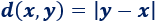
Ejemplo
La distancia entre \(2\) y \(6\) es \(4\):

Representación:

Las siguientes propiedades son fáciles de ver:
- La distancia de \(x\) a \(y\) es igual a la distancia de \(y\) a \(x\) (propiedad simétrica):
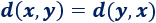
- La distancia entre dos puntos es siempre no negativa (es un valor absoluto):
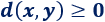
Estas propiedades se mantienen para dimensiones mayores.
Problema 1
Representar y calcular la distancia entre los puntos \(6\) y \(-2\) de la recta.
Solución:
La distancia entre \(6\) y \(-2\) es \(8\):
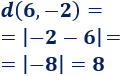
Representación:

Problema 2
Representar y calcular la distancia entre los puntos \(-4\) y \(-8\) de la recta.
Solución:
La distancia entre \(-4\) y \(-8\) es \(4\):
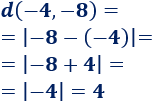
Representación:

2. Distancia en \(\mathbb{R}^2\)
Sean \((a, b)\) e \((x,y )\) dos puntos de \(\mathbb{R}^2\), se define la distancia de \((a, b)\) a \((x,y )\) como
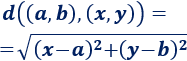
Es decir, la distancia es la raíz cuadrada de la suma de los cuadrados de la diferencia de las coordenadas de los puntos.
Ejemplo 1
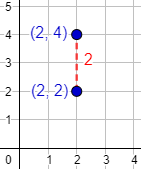
La distancia entre los puntos \((2, 2)\) y \((2, 4)\) es \(2\):
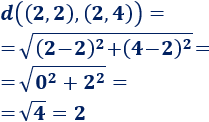
Representación:
Ejemplo 2
La distancia entre los puntos \((0, 1)\) y \((2, 2)\) es \(\sqrt{5} \simeq 2.24\):
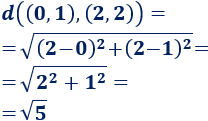
Representación:
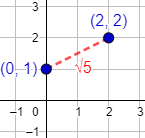
Observad que la distancia es la longitud del segmento que une ambos puntos.
Problema 3
Representar y calcular la distancia entre los puntos \((-2,6)\) y \((-5,2)\) del plano.
Solución:
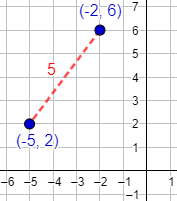
La distancia entre los puntos \((-2, 6)\) y \((-5, 2)\) es \(5\):
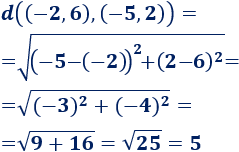
Representación:
Problema 4
Representar y calcular la distancia entre los puntos \((2,4)\) y \((-2,4)\) del plano.
Solución:
Aplicamos la fórmula:
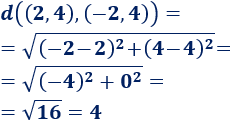
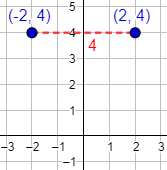
Representación:
Problema 5
Representar todos los puntos del plano real cuya distancia al punto \((2,2)\) sea igual a \(1\).
Solución:
Los puntos que distan \(1\) del punto \((2,2)\) es la circunferencia de centro \((2,2)\) y radio \(r=1\):
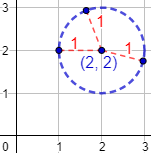
Recordad que la distancia de cualquier punto de la circunferencia a su centro es igual al radio, que en nuestro caso es \(r=1\).
La ecuación de la circunferencia es
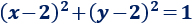
Por ejemplo, los siguientes puntos forman parte de dicha circunferencia:
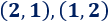
Ya que verifican la ecuación:
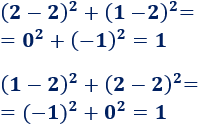
3. Distancia en \(\mathbb{R}^3\)
Sean \((a, b, c)\) e \((x, y, z )\) dos puntos de \(\mathbb{R}^3\), se define la distancia de \((a, b, c)\) a \((x, y, z )\) como
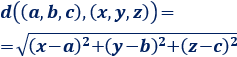
Ejemplo
La distancia entre los puntos \((1,1,1)\) y \((1,2,3)\) es \(\sqrt{5}\):
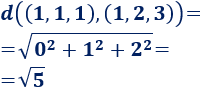
Problema 6
Calcular la distancia entre los puntos \((1,2,4)\) y \((4,2,1)\) del espacio.
Solución:
Aplicamos la fórmula:
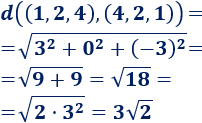
Hemos simplificado el resultado extrayendo un \(3\) de la raíz.