Vectores 2D (vectores de \(\mathbb{R}^2\))
En esta página resolvemos problemas de vectores bidimensionales del plano, es decir, vectores de \(\mathbb{R}^2\), mientras recordamos los conceptos básicos y las operaciones.
Índice de contenidos:
- Escalar y vector
- Suma y resta de vectores
- Producto de un escalar por un vector
- Módulo de un vector
- Producto escalar de vectores
- Vector unitario
- Ángulo entre vectores
En la siguiente página podéis encontrar más problemas y calculadoras de vectores 2D: Vectores del plano real.
Escalar y vector
Un escalar \(\alpha\) es cualquier número real. Es decir, \(\alpha \in\mathbb{R}\).
Un vector \(\vec{v}\) de \(\mathbb{R}^2\) es \(\vec{v}=(x,y)\), siendo \(x\) e \(y\) números reales, llamados primera y segunda coordenada, respectivamente, del vector.
Suma y resta de vectores
La suma y la resta de los vectores \(\vec{v}=(x,y)\) y \(\vec{w}=(a,b)\) son los siguientes vectores:
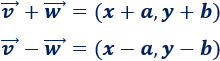
Problema 1
Calcular las siguientes sumas y restas de vectores:
-
\(\vec{v}+\vec{w}\)
-
\(\vec{v}+\vec{v}\)
-
\(\vec{w}-\vec{w}\)
-
\(\vec{w}-\vec{v}\)
siendo \(\vec{v} = (1,-2)\) y \(\vec{w} = (-5,0)\).
Solución:
La suma se calcula sumando coordenada a coordenada. La resta, restando las coordenas.
-
\(\vec{v}+\vec{w}\)
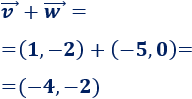
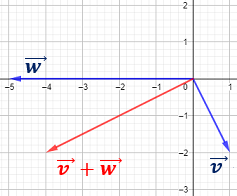
Representación:
-
\(\vec{v}+\vec{v}\)
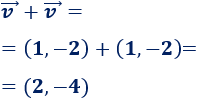
Representación:
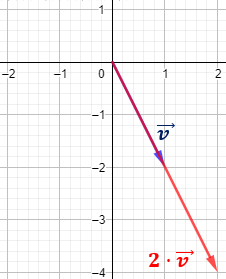
Observad que el resultado es el mismo que el de \(2·\vec{v}\).
-
\(\vec{w}-\vec{w}\)
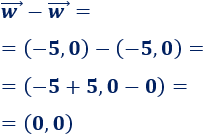
-
\(\vec{w}-\vec{v}\)
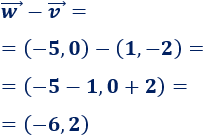
Representación:
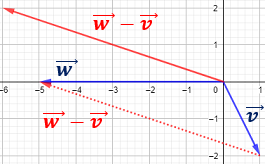
El vector que se obtiene es el que va de \(\vec{v}\) a \(\vec{w}\).
Problema 1b
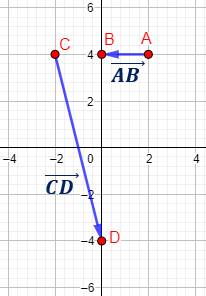
Calcular y representar el vector que va del punto \(A = (2,4)\) al punto \(B=(0,4)\) y el vector que va del punto \(C = (-2,4)\) al punto \(D=(0,-4)\).
Solución:
El vector que va del punto \(A\) al punto \(B\) es el vector cuyas coordenadas son la resta de las coordenadas de \(B\) menos las de \(A\).
El vector que va del punto \(A = (2,4)\) al punto \(B=(0,4)\) es
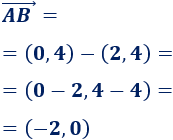
El vector que va del punto \(C = (-2,4)\) al punto \(D=(0,-4)\) es
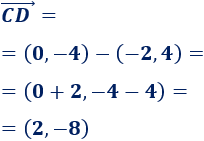
Representación:
Producto de un escalar por un vector
El producto de un escalar \(\alpha\) por un vector \(\vec{v}=(x,y)\) tiene como resultado el vector
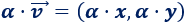
Problema 2
Calcular los siguientes productos de escalares por vectores:
-
\(3·\vec{v}\)
-
\(-2·\vec{w}\)
-
\(0·\vec{v}\)
siendo \(\vec{v} = (5,-2)\) y \(\vec{w} = (3,1/2)\).
Solución:
-
\(3·\vec{v}\)
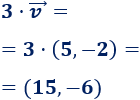
-
\(-2·\vec{w}\)
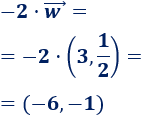
-
\(0·\vec{v}\)
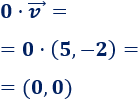
Problema 3
Comprobad que el producto de un escalar por un vector es distributivo respecto de la suma (y resta) de vectores. Es decir, si \(\alpha\) es un escalar y \(\vec{v}=(x,y)\) y \(\vec{w}=(a,b)\) son vectores, entonces
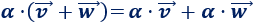
Solución:
Calculamos la suma de los dos vectores:
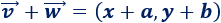
Por tanto, el lado de la izquierda es
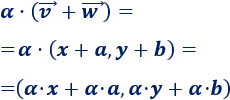
Calculamos los productos y la suma del lado derecho:
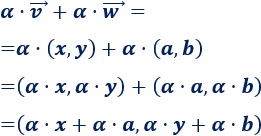
Los dos resultados coinciden.
Módulo de un vector
El módulo de un vector \(\vec{v}=(x,y)\) es la raíz cuadrada de la suma de los cuadrados de sus coordenadas:
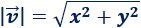
El módulo de un vector es su longitud (lo podéis comprobar aplicando el Teorema de Pitágoras).
Dado un escalar \(\alpha\), se cumple
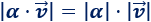
Problema 4
Calcular el módulo de los siguientes vectores:
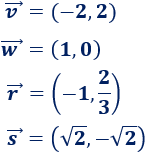
Solución:
-
Módulo de \(\vec{v}\):
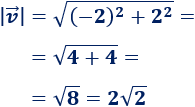
-
Módulo de \(\vec{w}\):
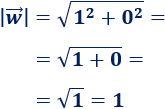
-
Módulo de \(\vec{r}\):
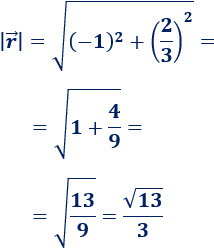
-
Módulo de \(\vec{s}\):
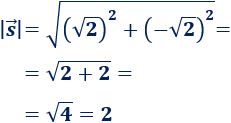
Problema 5
Representar los dos siguientes vectores y calcular sus módulos:
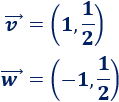
Solución:
-
Calculamos el módulo de \(\vec{v}\):
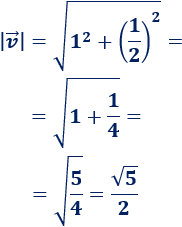
-
Calculamos el módulo de \(\vec{w}\):
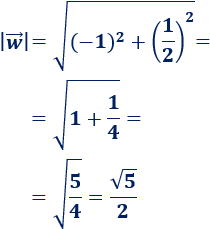
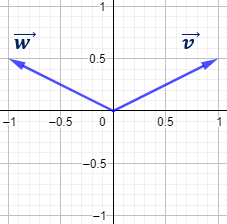
Los dos vectores tienen el mismo módulo (miden lo mismo), pero son vectores distintos. De hecho, uno de ellos es el vector simétrico del otro respecto del eje vertical OY.
Representación:
Producto escalar de vectores
El producto escalar de dos vectores \(\vec{v}=(x,y)\) y \(\vec{w}=(a,b)\) es el escalar
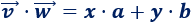
Si el ángulo que forman los dos vectores es \(\alpha\), también podemos calcular el producto escalar a partir de sus módulos y del ángulo:

Problema 6
Calcular el producto escalar de los siguientes pares de vectores:
-
\(\vec{v}=(1,2)\) y \(\vec{w}=(0,2)\)
-
\(\vec{v}=(3,-2)\) y \(\vec{w}=(-2,3)\)
-
\(\vec{v}=(1/2,9)\) y \(\vec{w}=(4,1/3)\)
Solución:
El producto se calcula multiplicando las coordenadas y sumando:
-
\(\vec{v}=(1,2)\) y \(\vec{w}=(0,2)\)
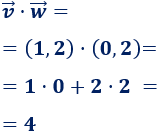
-
\(\vec{v}=(3,-2)\) y \(\vec{w}=(-2,3)\)
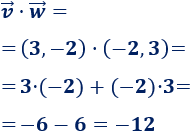
-
\(\vec{v}=(1/2,9)\) y \(\vec{w}=(4,1/3)\)
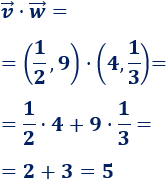
Vector unitario
El vector unitario de un vector \(\vec{v}\neq 0\) es
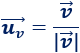
Este vector tiene la misma dirección y sentido que \(\vec{v}\), pero módulo 1.
Problema 7
Calcular el vector unitario de los vectores \(\vec{v} = (1,-3)\) y \(\vec{w} = (1/2,2)\).
Solución:
El vector unitario de un vector se calcula dividiendo el vector entre su módulo.
-
Calculamos el módulo de \(\vec{v}\):
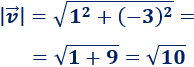
Su vector unitario es:
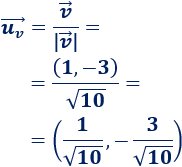
-
Calculamos el módulo de \(\vec{w}\):
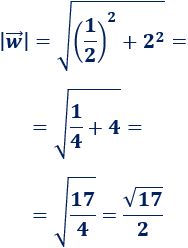
Su vector unitario es:
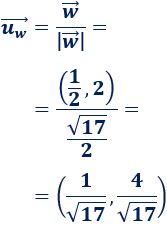
Problema 8
Calcular el vector \(\vec{w}\) que tiene el mismo sentido y la misma dirección que \(\vec{v} = (4,3)\), pero cuyo módulo sea igual a 2/5.
Ayuda: utilizar la propiedad del módulo de un escalar \(\alpha\) por un vector \(\vec{v}\):
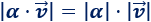
Solución:
Primero calculamos el módulo de \(\vec{v}\):
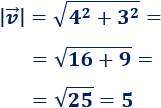
Si dividimos las coordenadas de \(\vec{v}\) entre su módulo, obtenemos un vector igual que \(\vec{v}\), pero con módulo unitario (módulo igual a 1):
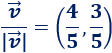
Por la propiedad, si multiplicamos el vector por \(2/5\), el nuevo vector tiene módulo \(2/5\):
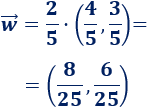
Ángulo entre vectores
Teniendo en cuenta las dos fórmulas del producto escalar de los vectores \(\vec{v}=(x,y)\) y \(\vec{w}=(a,b)\), tenemos el coseno del ángulo:
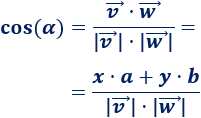
Podemos calcular el ángulo \(\alpha\) que forman los vectores con el arcocoseno.
Problema 9
Indicar si los siguientes pares de vectores son perpendiculares (el ángulo que forman entre ellos es de 90 grados):
-
\(\vec{v}=(-1,3)\) y \(\vec{w}=(3,1)\)
-
\(\vec{v}=(2/3,-7/2)\) y \(\vec{w}=(-21,-4)\)
-
\( \vec{v}=(1,1)\) y \(\vec{w}=(2,-1)\)
-
\( \vec{v}=(5,1)\) y \(\vec{w}=(0.5,-2.5)\)
Solución:
Recordad la segunda fórmula del producto escalar:

Como el coseno de \(90^\circ\) es \(0\), los vectores son perpendiculares cuando su producto escalar es \(0\):

Así que sólo tenemos que ver si el producto escalar de los vectores es \(0\).
-
Producto escalar de \(\vec{v}=(-1,3)\) y \(\vec{w}=(3,1)\):
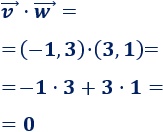
Los dos vectores son perpendiculares.
Representación:
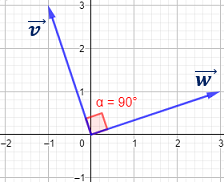
-
Producto escalar de \(\vec{v}=(2/3,-7/2)\) y \(\vec{w}=(-21,-4)\):
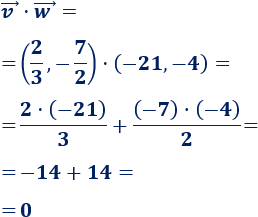
Los dos vectores son perpendiculares.
-
Producto escalar de \( \vec{v}=(1,1)\) y \(\vec{w}=(2,-1)\):
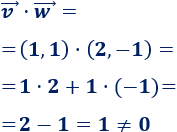
Los dos vectores no son perpendiculares.
Representación:
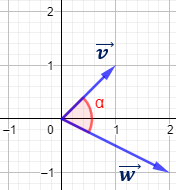
-
Producto escalar de \( \vec{v}=(5,1)\) y \(\vec{w}=(0.5,-2.5)\):
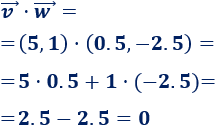
Los dos vectores son perpendiculares.
Problema 10
Comprobar que \(\vec{v_1}=(-y,x)\) y \(\vec{v_2}=(y,-x)\) son vectores perpendiculares al vector \(\vec{v}=(x,y)\).
Solución:
Como en el problema anterior, comprobamos si el producto escalar de los vectores es 0.
Primer par:
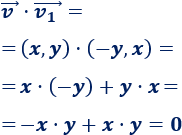
Segundo par:
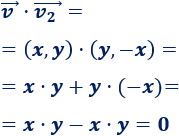
Observad que para calcular estos dos vectores perpendiculares a \(\vec{v}\) se ha cambiado el orden de las coordenadas y el signo de una de ellas.
Problema 11
Calcular el ángulo que forman los siguientes pares de vectores:
-
\(\vec{v}=(2,1)\) y \(\vec{w}=(1,3)\)
-
\(\vec{v}=(0,-6)\) y \(\vec{w}=(3,- \sqrt{3})\)
-
\(\vec{v}=(0,- \sqrt{3} )\) y \(\vec{w}=( \sqrt{3}/2, -3/2)\)
Solución:
Usamos la fórmula obtenida a partir del producto escalar:
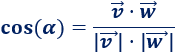
-
Ángulo entre \(\vec{v}=(2,1)\) y \(\vec{w}=(1,3)\)
Calculamos los módulos de los vectores:
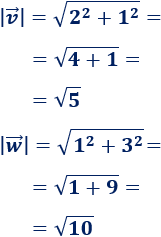
Calculamos el producto escalar:
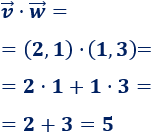
Aplicamos la fórmula:
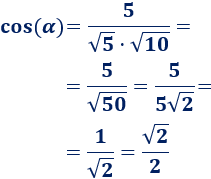
El coseno del ángulo \(\alpha\) que forman los vectores es \(\sqrt{2}/2\). Por tanto, \(\alpha = 45^\circ\).
Representación:
-
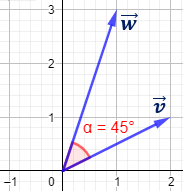
Ángulo entre \(\vec{v}=(0,-6)\) y \(\vec{w}=(3,- \sqrt{3})\)
Calculamos los módulos de los vectores:
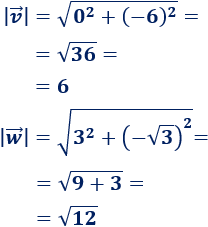
Calculamos el producto escalar:
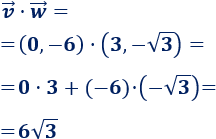
Aplicamos la fórmula:
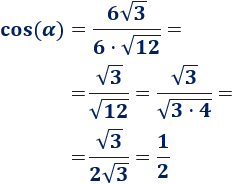
El coseno del ángulo \(\alpha\) que forman los vectores es \(1/2\). Por tanto, \(\alpha = 60^\circ\).
Representación:
-
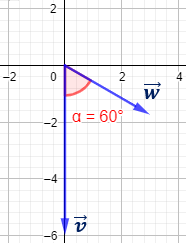
Ángulo entre \(\vec{v}=(0,- \sqrt{3} )\) y \(\vec{w}=( \sqrt{3}/2, -3/2)\)
Calculamos los módulos de los vectores:
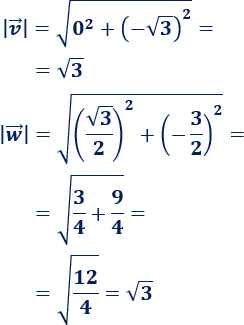
Calculamos el producto escalar:
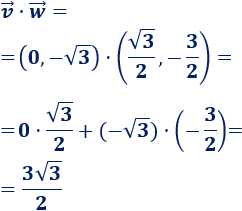
Aplicamos la fórmula:
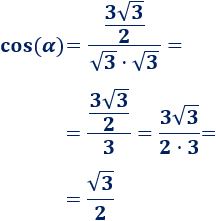
El coseno del ángulo \(\alpha\) que forman los vectores es \(\sqrt{3}/2\). Por tanto, \(\alpha = 30^\circ\).
Representación:
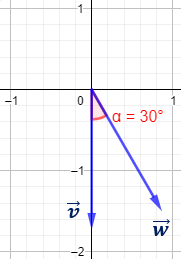
Problema 12
Aproximar el ángulo que forman los vectores \(\vec{v}=(1,-1)\) y \(\vec{w}=(-2, 3)\) entre sí.
Solución:
Procedemos como en el problema anterior.
Calculamos los módulos de los vectores:
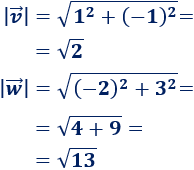
Calculamos el producto escalar:
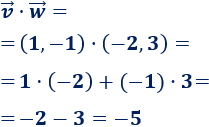
Aplicamos la fórmula:
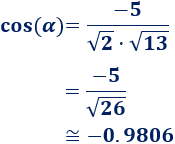
Aplicamos el arcocoseno para calcular el ángulo:
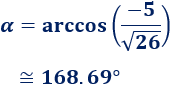
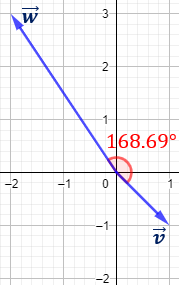
Representación:
Más problemas resueltos de vectores 2D:
- Sumar y restar vectores
- Módulo de un vector
- Diferencias entre módulo, dirección y sentido
- Vector que une dos puntos
- Producto de un vector por un escalar
- Producto escalar de vectores
- Vectores del plano (resumen)
- Calculadora del módulo, producto escalar y ángulo