¿La circunferencia es la gráfica de una función?
Las rectas o las parábolas son ejemplos de conjuntos del plano que pueden verse como la gráfica de una función, pero ¿una circunferencia también puede ser la gráfica de una función?
Como primera respuesta a esta pregunta, diremos que no, la circunferencia no puede ser la gráfica de una función y a continuación veremos por qué y cómo representar una circunferencia mediante funciones.
Índice:
- Circunferencia como conjunto del plano
- La circunferencia como gráfica
- Semicircunferencia como gráfica
- La distancia de los puntos al centro es el radio
- Problemas resueltos
1. Circunferencia como conjunto del plano
La circunferencia de radio \(R > 0\) y centro \(P = (a, b)\) es el conjunto de puntos \((x,y)\) del plano tales que
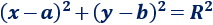
Dicho en otras palabras, son los puntos que distan \(R\) del punto \(P\).
Representación gráfica:
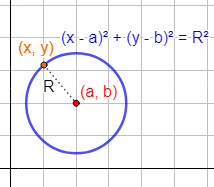
2. La circunferencia como gráfica
Para ver que una circunferencia no puede ser la gráfica de una única función, pensemos en la circunferencia de centro \((0,0)\) y radio \(R = 1\), cuya ecuación es \(x^2+y^2 = 1\):
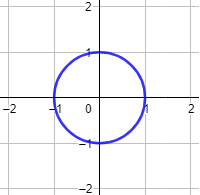
Es fácil de ver que los puntos \((0,1)\) y \((0,-1)\) pertenecen a la circunferencia, pues verifican su ecuación:
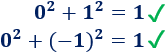
Representación:
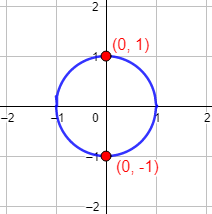
Ahora, recordemos que la gráfica de una función son los puntos (\(\alpha ,f(\alpha)\)).
Si suponemos que existe una función cuya gráfica sea la circunferencia en cuestión, entonces dicha función debería tener dos imágenes distintas para 0:
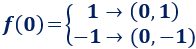
Y sabemos que
Una función tiene una ÚNICA imagen para cada punto de su dominio.
Por tanto, no puede haber una función cuya gráfica sea una circunferencia.
3. Semicircunferencia como gráfica
Ahora bien, podemos considerar la circunferencia como dos semicircunferencias:
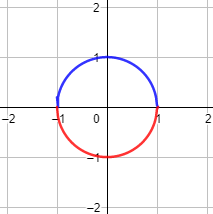
En este caso, las dos semicircunferencias sí pueden ser las gráficas de dos funciones (\(f\) y \(g\)) y dichas funciones podemos obtenerlas de la propia ecuación de la circunferencia. Sólo tenemos que aislar \(y\):
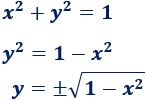
Las funciones serían, pues,
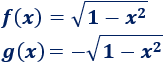
Y el dominio de ambas funciones debe ser el intervalo \([-1,1]\).
4. La distancia de los puntos al centro es el radio
Vamos a comprobar que, en efecto, los puntos de la circunferencia de centro \(P=(a,b)\) y radio \(R\) es exactamente \(R\).
Por un lado, la ecuación de la circunferencia referida es
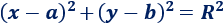
Por otro lado, la distancia (euclídea) entre el punto \((a,b)\) y cualquier punto \((\alpha ,\beta )\) es
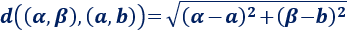
Ahora bien, si \((x ,y)\) es un punto de la circunferencia, entonces verifica la ecuación y, por tanto,
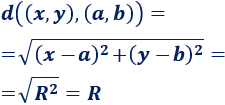
Luego la distancia de cualquier punto de la circunferencia al centro es exactamente el radio.
5. Problemas resueltos
Problema 1
¿Existe alguna función cuya gráfica sea un triángulo? Razonar la respuesta.
Solución:
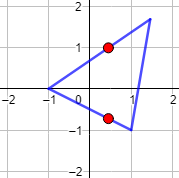
Figura: los dos puntos rojos comparten la primera coordenada.
Al igual que ocurre con la circunferencia, dicha función debería tener imágenes distintas para algunos puntos de su dominio, así que no es posible.
Sí puede verse como la gráfica de tres funciones lineales (su gráfica es una recta).
Problema 2
Comprobar si los puntos (0, 1) y (1, 1) forman parte de la circunferencia de centro (1, -1) y radio 2.
Solución:
La ecuación de la circunferencia de centro (1,-1) y radio 2 es
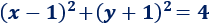
Sustituimos las coordenadas de los puntos para ver si están en la circunferencia.
Punto (0, 1):
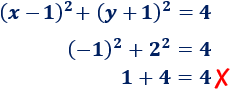
No verifica la ecuación, así que no está en la circunferencia.
Punto (1, 1):
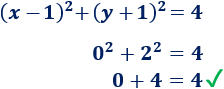
Sí verifica la ecuación, así que este punto está en la circunferencia.
Representación:
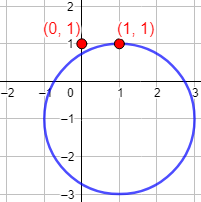
Problema 3
¿Cuál es la ecuación del círculo de radio 1 y centro (0, 0)?
Solución:
La representación del círculo es
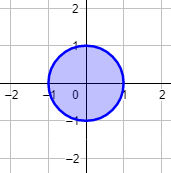
Obviamente, los puntos de la circunferencia que comparte centro y radio con el círculo también están en el círculo. De hecho, son los puntos del borde del círculo.
Los puntos interiores (los que no están en el borde) están más cerca del centro del círculo.
Si los puntos del borde distan \(R = 1\) del centro, los del interior están situados a una distancia menor que \(R\).
Por tanto, todos los puntos del círculo se sitúan a una distancia menor o igual que \(R=1\) del centro, por lo que la ecuación del círculo es
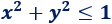
Sólo hemos cambiado el signo = de la ecuación de la circunferencia por el signo ≤.
Problema 4
Hallar la expresión analítica de la función que tiene como gráfica la semicircunferencia superior de centro (1, 2) y radio 1.
Solución:
La ecuación de la circunferencia de centro (1, 2) y radio 1 es
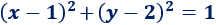
Para obtener su semicircunferencia superior, despejamos \(y\):
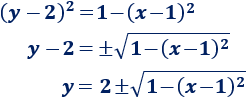
Como queremos la semicircunferencia superior, la función es
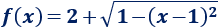
O bien, desarrollando el cuadrado,
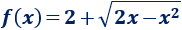
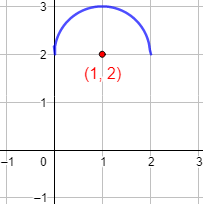
Gráfica:
Otros temas relacionados:
- Ecuación de la circunferencia
- Área del círculo
- Perímetro
- ¿Qué es una ecuación?
- ¿Todas las ecuaciones tienen solución?
- ¿Cuántas soluciones tiene una ecuación?
- ¿Hay ecuaciones sin solución?
- ¿Por qué se dice al cuadrado y al cubo?
- Pasar de un lado a otro de la igualdad
Problemas y Ecuaciones ©
ISSN 2659-9899