Fracciones con signos
En esta página estudiamos las fracciones con signos, especialmente, con signos negativos. Veremos que una fracción puede tener varios o ningún signo, aunque es recomendable utilizar el mínimo número posible. Con ejemplos y problemas resueltos.
Índice:
- Conceptos necesarios
- Signo de una fracción
- Fracciones con varios signos
- Significado de una fracción negativa
- Problemas resueltos
1. Conceptos necesarios
Una fracción está formada por dos números (numerador y denominador) separados por una raya:

Recordad:
- El denominador nunca puede ser \(0\), es decir, \(b \neq 0\).
- La fracción \(a/b\) es el cociente \(a\) dividido entre \(b\).
- La fracción \(a/b\) puede verse como \(a\) trozos de un todo que se ha dividido en \(b\) trozos iguales.
Ejemplo
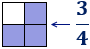
Consideremos la fracción \(3/4\) (tres cuartos):
- Su numerador es \(3\).
- Su denominador es \(4\).
- Es igual a \(0,75\) porque \(3\) dividido entre \(4\) es \(0,75\).
- Si dividimos un todo en \(4\) trozos iguales, la fracción \(3/4\) se corresponde con \(3\) de los \(4\) trozos:
2. Signo de una fracción
Las fracciones son, en realidad, números y, por tanto, también pueden tener signo positivo o negativo.
- Si la fracción es positiva, no suele escribirse el signo. Por ejemplo,
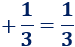
- Esto también lo hacemos con los números enteros positivos:
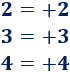
- Si la fracción es negativa, el signo suele escribirse delante. Por ejemplo,
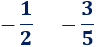
- No obstante, podemos encontrar el signo situado en el numerador o en el denominador:
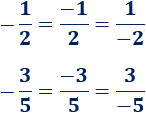
- Si es posible, debemos optar por escribir el signo delante de la fracción.
También, podemos encontrar signos positivos, aunque no es habitual:
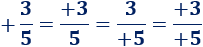
3. Fracciones con varios signos
A veces, encontramos fracciones con varios signos. Por ejemplo,
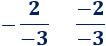
En estos casos, es posible reescribir la fracción con único signo o ninguno. Para ello, tenemos que recordar la regla de los signos:
- La multiplicación o la división de dos números con igual signo es positiva.
- La multiplicación o la división de dos números con signos distintos es negativa.
De este modo, para modificar o quitar los signos de una fracción tenemos que aplicar la regla de los signos porque una fracción es una división.
Ejemplos
- La división de dos números negativos es positiva:
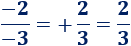
- La división de dos números con signos distintos es negativa:
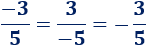
- Si tenemos dos signos negativos, la fracción es positiva (negativo entre negativo es positivo):
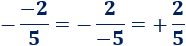
- La siguiente fracción también es negativa, aunque en ella aparecen dos signos positivos y uno negativo:
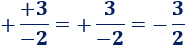
4. Significado de una fracción negativa
Si consideramos que una fracción es un trozo o una parte de un todo, es complicado pensar en una fracción negativa, pero algo similar ocurre con los enteros negativos.
Veamos un ejemplo para darle sentido a las fracciones negativas.
Supongamos que tenemos una pizza y la dividimos en \(4\) trozos. Cada uno de estos trozos es un cuarto de pizza, es decir, la fracción \(1/4\):
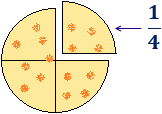
La pizza entera son cuatro cuartos:
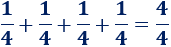
Caso 1
Si tenemos la pizza entera (\(4\) trozos) y cogemos \(2\) trozos, nos quedan otros \(2\) (quedan dos cuartos):
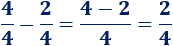
Caso 2
Si de los \(2\) trozos de pizza que tenemos, queremos coger \(3\), nos faltaría un trozo (faltaría un cuarto):
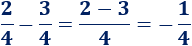
En este ejemplo, podemos ver la fracción negativa como la fracción de una cantidad que nos falta.
5. Problemas resueltos
Problema 1
Escribir las siguientes fracciones con un único signo o ninguno:
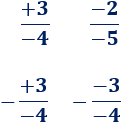
Solución:
Recordad que es aconsejable escribir el signo delante. Aplicaremos la regla de los signos.
Primera fracción:
La fracción es negativa porque es la división de un número positivo entre uno negativo:
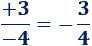
Segunda fracción:
La fracción es positiva porque es la división de dos números con igual signo:
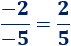
Tercera fracción:
La fracción es positiva, ya que hay un signo negativo delante de una división de números con signos distintos, la cual tiene resultado negativo:
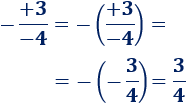
Cuarta fracción:
Razonando de forma similar, la fracción es negativa:
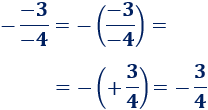
Problema 2
Sin necesidad de calcular la siguiente multiplicación, ¿el resultado es positivo o negativo?
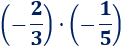
Solución:
Tenemos la multiplicación de dos fracciones con el mismo signo (signo negativo), por tanto, el resultado es positivo:
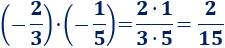
Problema 3
Calcula las siguientes restas de fracciones:

Solución:
Como los denominadores son iguales, sólo hay que restar los numeradores.
Primera resta:
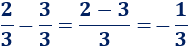
Segunda resta:
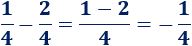
Problema 4
¿Sabrías calcular la siguiente suma de fracciones?
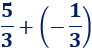
Solución:
En realidad, sumar un número negativo con uno negativo es lo mismo que restar los dos números (el positivo menos el negativo):
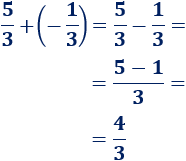
Problema 5
¿Cuál es el resultado de dividir una fracción positiva entre una fracción negativa?
Solución:
Por la regla de los signos, como los signos son distintos, el resultado es negativo.
Otros temas relacionados:
- Fracciones equivalentes
- Operaciones con fracciones
- Multiplicar fracciones
- Número por paréntesis
- Paréntesis por paréntesis
- Regla de los signos
- ¿Qué es una ecuación?
- ¿Todas las ecuaciones tienen solución?
- ¿Cuántas soluciones tiene una ecuación?
- ¿Hay ecuaciones sin solución?
- ¿Por qué se dice al cuadrado y al cubo?
- Pasar de un lado a otro de la igualdad
Problemas y Ecuaciones ©
ISSN 2659-9899