Multiplicación de fracciones
\( \frac{a}{b}\cdot \frac{c}{d} = \frac{a\cdot c}{ b\cdot d}\)
Dedicamos esta página exclusivamente a la multiplicación de fracciones. Explicamos cómo realizar esta operación con ejemplos y problemas resueltos. También, veremos algunas propiedades relacionadas.
Índice:
- Conceptos necesarios
- Multiplicación o producto de fracciones
- Propiedad conmutativa
- Simplificar el resultado
- Fracción por un número
- Problemas resueltos
1. Conceptos necesarios
Una fracción es expresión algebraica formada por dos números separados por una raya:

Recordemos algunas nociones:
- El denominador NUNCA puede ser \(0\), es decir, \(b\neq 0\).
- La fracción \(a/b\) es el cociente de la división \(a\) dividido entre \(b\). Por ejemplo,
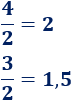
- Numerador y denominador pueden ser negativos. Por ejemplo,
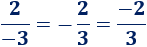
- Dos fracciones formadas por números distintos pueden ser iguales (son fracciones equivalentes), por ejemplo,
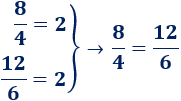
- Como \(8/4 = 2\) y \(12/6 = 2\), entonces \(8/4 = 12/6\).
- La fracción \(a/b\) significa \(a\) de cada \(b\). Por ejemplo, la fracción \(2/9\) son \(2\) de \(9\) partes, porciones o fracciones:
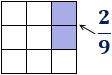
- Nota: cada cuadrado es la fracción \(1/9\).
2. Multiplicación o producto de fracciones
La multiplicación de dos fracciones es la fracción que se obtiene multiplicando los numeradores y los denominadores:
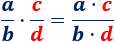
Es decir, tenemos que multiplicar "numerador por numerador" y "denominador por denominador".
También, podemos usar la \(\times\) para representar la multiplicación, aunque se recomienda usar el punto \(\cdot\):
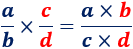
Ejemplos
- Multiplicamos las fracciones \(7/5\) y \(3/2\):
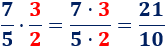
- Multiplicamos las fracciones \(2/3\) y \(2/5\):

Las fracciones pueden ser negativas o positivas, así que tenemos que tener en cuenta la regla de los signos.
Ejemplos
- Multiplicamos las fracciones \(-1/2\) y \(3/2\):
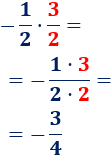
- Observad que la fracción del resultado es negativa porque hemos multiplicado una fracción negativa por una fracción positiva.
- Multiplicamos las fracciones \(2/3\) y \(-1/3\):
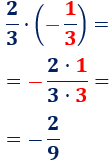
- Observad que la segunda fracción se escribe entre paréntesis porque tiene un signo negativo detrás del punto de multiplicación.
Si las fracciones tienen signos en el numerador o denominador, podemos calcular la multiplicación como una multiplicación de números enteros.
Ejemplo
Multiplicamos las fracciones \(2/(-3)\) y \(3/(-5)\):
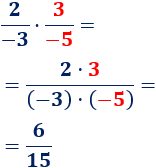
Podemos calcular la multiplicación de más de \(2\) fracciones usando la misma regla:
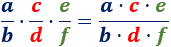
Ejemplo
Multiplicamos las fracciones \(2/3\), \(5/2\) y \(1/2\):
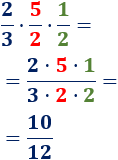
Nota: el resultado se puede simplificar: \(10/12 = 5/6\).
3. Propiedad conmutativa
La multiplicación de fracciones es una propiedad conmutativa:
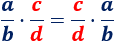
Ejemplo
Se obtiene el mismo resultado si cambiamos el orden de las fracciones en la multiplicación:

4. Simplificar el resultado
Siempre que sea posible, debemos simplificar el resultado. Esto se consigue dividiendo el numerador y el denominador de la fracción entre el máximo común divisor de éstos.
Ejemplo
Multiplicamos las fracciones \(2/5\) y \(3/4\):

Simplificamos el resultado dividiendo entre el máximo común divisor de \(6\) y \(20\), que es \(2\):

Recordad que la fracción que no se puede simplificar se denomina fracción irreducible (el máximo común divisor del numerador y denominador es \(1\)).
Otra forma de simplificar las fracciones es escribir numerador y denominador como multiplicaciones y cancelar los términos comunes.
Ejemplo
Escribimos \(6\) como \(2\cdot 3\) y \(4\) como \(2\cdot 2\) para cancelar los factores comunes:

5. Fracción por un número
Un número puede verse como una fracción cuyo denominador es \(1\).
Ejemplos
- El \(2\) es la fracción \(2/1\):
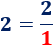
- El \(-3\) es la fracción \(-3/1\):
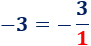
De esto modo, es fácil ver que la multiplicación de un número por una fracción se calcula multiplicando sólo al numerador:
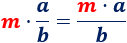
Ejemplo
Multiplicamos \(2\) por \(2/5\):
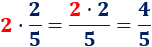
Si es necesario, se puede escribir el número como una fracción:
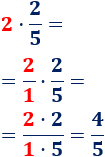
6. Problemas resueltos
Problema 1
Multiplicar las fracciones:
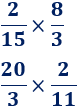
Solución:
Recordamos que debemos multiplicar los numeradores y los denominadores.
Primera multiplicación:
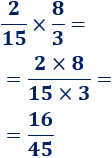
La fracción es irreducible (no se puede simplificar).
Segunda multiplicación:
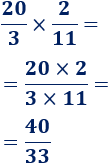
La fracción también es irreducible (no se puede simplificar).
Problema 2
Calcular las siguientes multiplicaciones (siendo \(a, b\neq 0\)):
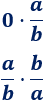
Solución:
La primera multiplicación da \(0\):
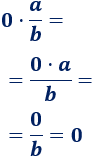
La segunda multiplicación da \(1\):
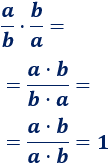
En el último paso hemos escrito que la fracción es igual a \(1\) porque el numerador y el denominador son iguales.
Nota: La fracción \(b/a\) se denomina fracción inversa de la fracción \(a/b\).
Problema 3
Multiplicar las fracciones:
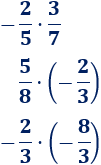
Solución:
Primera multiplicación:
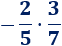
El resultado es una fracción negativa porque es el producto de una fracción negativa y una positiva:
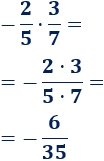
La fracción no se puede simplificar.
Segunda multiplicación:
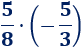
El resultado también es una fracción negativa porque es el producto de una fracción positiva y una negativa:
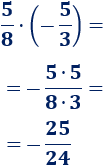
La fracción no se puede simplificar.
Tercera multiplicación:
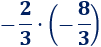
El resultado es una fracción positiva porque es el producto de dos fracciones negativas:
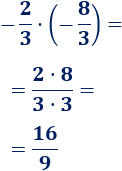
La fracción no se puede simplificar.
Problema 4
Multiplicar las fracciones:
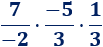
Solución:
Podemos calcular la multiplicación de las tres fracciones directamente, pero tenemos que tener en cuenta la regla de los signos:
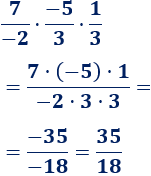
La fracción no se puede simplificar.
Problema 5
Multiplicar las fracciones y simplificar el resultado:
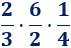
Solución:
Como tenemos que simplificar, es mejor no calcular las multiplicaciones en el numerador y el denominador:
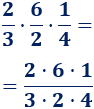
Podemos escribir \(6\) como \(2\cdot 3\) y \(4\) como \(2\cdot 2\):

Ahora, cancelamos los factores comunes del numerador y del denominador:
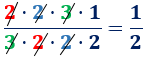
Problema 6
Multiplicar y simplificar:
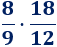
Solución:
Podemos multiplicar los números y después simplificar:
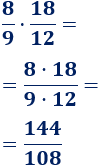
Para simplificar, debemos dividir numerador y denominador entre su máximo común divisor.
Escribimos el numerador y denominador en forma de potencias:
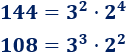
El máximo común divisor se calcula tomando las potencias cuya base es común y el exponente es menor:
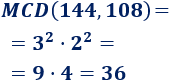
Simplificamos la fracción:
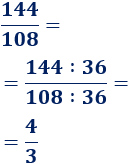
Otros temas relacionados:
- Fracciones equivalentes
- Operaciones con fracciones
- Número por paréntesis
- Paréntesis por paréntesis
- ¿Qué es una ecuación?
- ¿Todas las ecuaciones tienen solución?
- ¿Cuántas soluciones tiene una ecuación?
- ¿Hay ecuaciones sin solución?
- ¿Por qué se dice al cuadrado y al cubo?
- Pasar de un lado a otro de la igualdad
Problemas y Ecuaciones ©
ISSN 2659-9899