Monomios y polinomios
En esta página explicamos qué es un monomio, binomio, trinomio y polinomio y cómo sumar y restar monomios, con ejemplos y problemas resueltos. También, vemos los conceptos de grado de un monomio y de un polinomio y el de monomios semejantes.
Índice:
- Monomios
- Suma/resta de monomios
- Polinomios
- Problemas resueltos
Temas relacionados:
1. Monomios
Un monomio es una expresión algebraica formada por una parte numérica (coeficiente) y una parte literal.
Ejemplo
Señalamos el coeficiente y la parte literal de los tres monomios \(5xy\), \(-3x^2\) y \(4\):
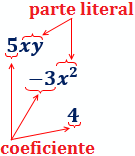
El tercer monomio no tiene parte literal.
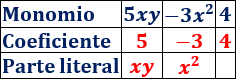
Podemos escribir el coeficiente y las letras como un producto. Por ejemplo,
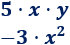
Si el coeficiente es \(1\), no es necesario escribirlo. Por ejemplo,

Las letras de la parte literal pueden tener exponente natural (\(1\), \(2\), \(3\),…). Por ejemplo,

Observad que el exponente \(3\) de \(5xy^3\) es sólo el exponente de \(y\):
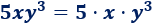
Si el exponente es \(1\), no es necesario escribirlo. Por ejemplo,
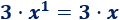
Si el exponente es \(0\), dicha letra no hay que escribirla. Por ejemplo,
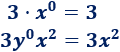
El grado de un monomio es la suma de los exponentes de su parte literal. Por ejemplo,
- El grado de \(5yx^2\) es \(3\) (el exponente de \(y\) es \(1\)).
- El grado de \(-2x\) es \(1\).
- El grado de \(2y^2x^2\) es \(4\).
- El grado de \(3\) es \(0\).
La parte numérica del monomio se denomina coeficiente y es positivo, negativo o neutro (si es el monomio \(0\)). Por ejemplo,
- El signo de \(-2x^3\) es negativo.
- El signo de \(3x\) es positivo.
Dos monomios son semejantes si tienen la misma parte literal (mismas letras y mismos exponentes). Por ejemplo,
- Los monomios \(2xy^2\) y \(3xy^2\) son semejantes.
- Los monomios \(3xy^2\) y \(5y^2x\) son semejantes (el orden de las letras no importa).
- Los monomios \(3xy^2\) y \(6x^2y\) no son semejantes.
2. Suma/resta de monomios
Si dos monomios tienen la misma parte literal, su suma se calcula sumando sus coeficientes.
Ejemplo

Los monomios tienen la misma parte literal: \(x·y^2\). La suma de sus coeficientes es \(3+5 = 8\). Por tanto,
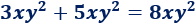
Si dos monomios tienen la misma parte literal, su resta se calcula restando sus coeficientes. Por ejemplo,

Si la parte literal es distinta, la suma/resta no puede escribirse como un solo monomio.
Ejemplo

No podemos simplificar la suma de estos dos monomios porque no tienen la misma parte literal: el exponente de la \(x\) del monomio de la izquierda es \(1\), mientras que en el de la derecha es \(2\).
Si la suma/resta de dos monomios tiene coeficiente \(0\), entonces no escribimos la parte literal, se trata de un monomio sin parte literal: el monomio \(0\). Por ejemplo,

Recordad que sumamos/restamos monomios cuando resolvemos ecuaciones. Por ejemplo,
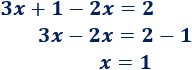
Observad que sumamos/restamos los monomios que tienen la misma parte literal.
3. Polinomios
Si dos monomios tienen distinta parte literal, su suma/resta no se puede escribir como un solo monomio. Esta suma/resta de dos monomios se denomina binomio.
Un trinomio es la suma/resta de tres monomios con distintas partes literales.
En general, la suma/resta de monomios con distintas partes literales se denomina polinomio.
Ejemplos
- Ejemplo de binomio:

- Ejemplo de trinomio:
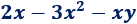
- Ejemplo de polinomio:
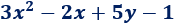
El grado de un polinomio es el mayor de los grados de sus monomios.
4. Problemas resueltos
Problema 1
Determinar el coeficiente, la parte literal y el grado de los siguientes monomios:
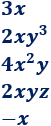
- ¿Cuáles de ellos son semejantes?
- Dar un ejemplo de monomio de grado \(0\).
Solución:
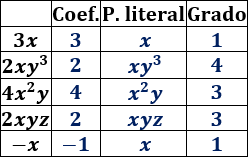
Sólo son semejantes el primer y el último monomio. Tienen la parte literal \(x\).
Los monomios de grado \(0\) son los que no tienen parte literal. Dos ejemplos de estos monomios son \(3\) y \(-5\).
Problema 2
Calcular, si es posible, las siguientes sumas y restas de monomios:
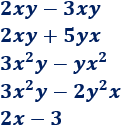
Solución:
Sólo podemos sumar/restar los que tienen la misma parte literal, que son los tres primeros:
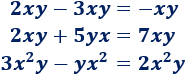
Problema 3
¿Cuáles de los siguientes polinomios son binomios o trinomios?
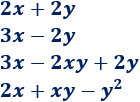
Solución:
Los dos primeros son binomios, los otros son trinomios.
Problema 4
¿Son iguales los siguientes binomios?
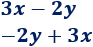
Solución:
Son iguales, sólo hay que cambiar el orden de los sumandos:
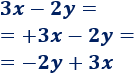
Problema 5
Sumar, si es posible, los tres siguientes monomios:
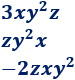
Solución:
La parte literal de los tres monomios es la misma, aunque cada uno de ellos tiene las letras escritas en distinto orden.
El resultado tiene coeficiente \(2\) porque 3+1-2 = 2 y tiene la misma parte literal:

Más problemas relacionados: