Multiplicar polinomios
Explicamos cómo multiplicar polinomios y proporcionamos algunos ejemplos.
Índice:
- Introducción
- Método
- Problemas resueltos
1. Introducción
Recordad que un polinomio es una suma finita de monomios de distinto grado.
Ejemplos
Ejemplo de un trinomio (polinomio formado por tres monomios):

Ejemplo de un binomio (polinomio formado por dos monomios):
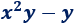
A continuación, vamos a ver cómo multiplicar dos polinomios.
2. Método
La multiplicación de dos polinomios se calcula multiplicando todos los monomios de uno de los polinomios (incluidos los signos) por todos los monomios del otro polinomio.
Después, tenemos que simplificar el resultado sumando los monomios que tienen la misma parte literal (los números con los números, las \(x\) con las \(x\), las \(x^2\) con las \(x^2\), etc.).
Ejemplo 1
Multiplicación de dos binomios:
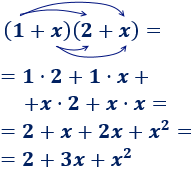
Ejemplo 2
Multiplicación de dos binomios con signos negativos:
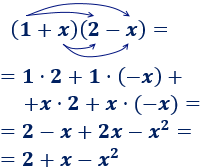
Nota: observad que al multiplicar polinomios, el grado del polinomio del resultado es la suma de los grados de los polinomios multiplicados.
3. Problemas resueltos
Problema 1
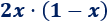
Solución:
Tenemos que multiplicar un monomio por un binomio. El monomio \(2x\) multiplica a los dos monomios de dentro del paréntesis:
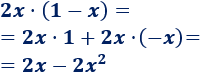
Nota: al multiplicar el monomio y el binomio de grado 1 se obtiene un binomio de grado 1+1 = 2.
Problema 2
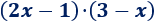
Solución:
Tenemos que multiplicar dos binomios: cada uno de los monomios del paréntesis de la izquierda debe multiplicar a cada uno de los monomios del paréntesis de la derecha:
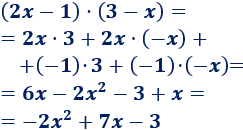
Nota: al multiplicar los binomios de grado 1 se obtiene un polinomio de grado 1+1 = 2.
Problema 3
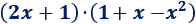
Solución:
Tenemos que multiplicar un binomio por un trinomio. El procedimiento es el mismo que en los problemas anteriores, pero ahora tenemos que calcular más multiplicaciones.
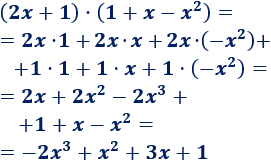
Nota: al multiplicar el binomio de grado 1 y el trinomio de grado 2 se obtiene un polinomio de grado 1+2 = 3.
Problema 4
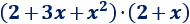
Solución:
Tenemos que multiplicar un trinomio por un binomio:
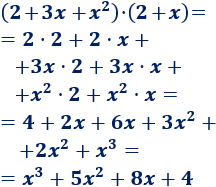
Nota: al multiplicar el trinomio de grado 2 y el binomio de grado 1 se obtiene un polinomio de grado 2+1 = 3.
Problema 5
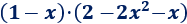
Solución:
Tenemos que multiplicar un binomio por un trinomio:
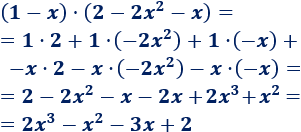
Nota: al multiplicar el binomio de grado 1 y el trinomio de grado 2 se obtiene un polinomio de grado 1+2 = 3.
Más problemas similares: multiplicar polinomios.