Suma y resta al cuadrado

Explicamos cómo calcular el cuadrado de una suma y de una resta a partir de las fórmulas. Con ejemplos y problemas resueltos.

El cuadrado de una suma no es la suma de los cuadrados. Por ejemplo,

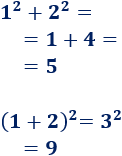
Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

Es decir, como regla general,

la suma de los cuadrados NO es igual al cuadrado de la suma:

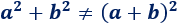
Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

Índice:

Suma al cuadrado
Resta al cuadrado
Problemas resueltos

1. Suma al cuadrado

La fórmula para calcular el cuadrado de una suma es

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

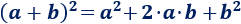
Esto es, el cuadrado de la suma de dos números es igual a la suma de sus cuadrados más el doble de su producto.

Demostramos esta fórmula en el Problema 8.

Ejemplo

Para calcular el cuadrado \((3+x)^2\), identificamos los dos sumandos y aplicamos la fórmula.

Llamaremos \(a = 3\) y \(b = x\), entonces:

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

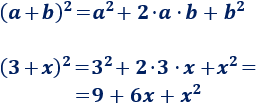
2. Resta al cuadrado

La fórmula para calcular el cuadrado de una resta es

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

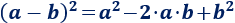
Demostramos esta fórmula en el Problema 9.

Ejemplo

Calculamos el cuadrado \((x-3)^2\) aplicando la fórmula, considerando \(a = x\) y \(b = 3\):

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

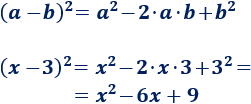
3. Problemas resueltos

Problema 1

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

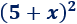
Solución:

Aplicamos la fórmula de la suma:

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

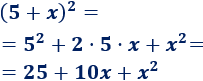
Problema 2

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

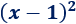
Solución:

Aplicamos la fórmula de la resta:

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

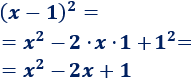
Problema 3

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

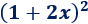
Solución:

Hay que tener en cuenta que el segundo sumando es \(b = 2x\) y, por tanto, su cuadrado es

\(b^2 = (2x)^2 =4x^2\)

Aplicamos la fórmula:

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

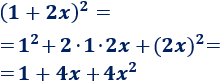
Problema 4

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

Solución:

Aplicamos la fórmula de la resta:

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

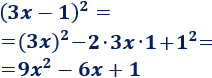
Problema 5

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

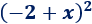
Solución:

Podemos cambiar el orden de los sumandos si así nos resulta más fácil aplicar la fórmula:

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

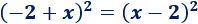
Aplicamos la fórmula de la resta:

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

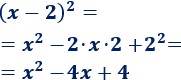
Problema 6

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

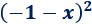
Solución:

Como hay dos signos negativos, podemos considerar \(a = -1\) y \(b=x\):

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

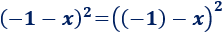
Aplicamos la fórmula de la resta:

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

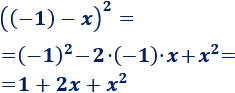
Problema 7

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

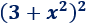
Solución:

Aplicamos la fórmula de la suma:

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

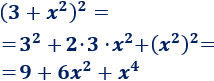
Problema 8

Demostrar la fórmula del cuadrado de la suma.

Solución:

Sólo tenemos que calcular la potencia como una multiplicación:

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

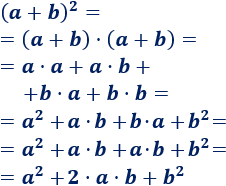
Hemos utilizado la propiedad conmutativa de la multiplicación:

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

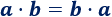
Problema 9

Demostrar la fórmula del cuadrado de la resta.

Solución:

Sólo tenemos que calcular la potencia como una multiplicación:

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

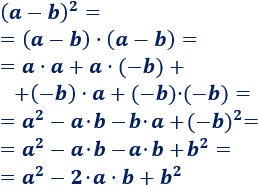
Problema 10

Encontrar dos números \(a\) y \(b\) para los cuales sea cierta la igualdad

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

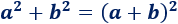
Solución:

Esta fórmula se cumple, por ejemplo, para los números \(1\) y \(0\):

Explicamos cómo calcular el cuadrado de una suma y de una resta: (a+b)^2 = a^2 + 2ab + b^2 y (a-b)^2 = a^2 -2ab + b^2. Con ejemplos y problemas resueltos. Álgebra. Matemáticas. Secundaria.

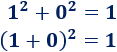
Más problemas similares: cuadrado y cubo de un binomio.

Suma y resta al cuadrado

la suma de los cuadrados NO es igual al cuadrado de la suma:

1. Suma al cuadrado

Ejemplo

2. Resta al cuadrado

Ejemplo

3. Problemas resueltos

Problema 1

Solución:

Problema 2

Solución:

Problema 3

Solución:

Problema 4

Solución:

Problema 5

Solución:

Problema 6

Solución:

Problema 7

Solución:

Problema 8

Solución:

Problema 9

Solución:

Problema 10

Solución:

Problemas y Ecuaciones ©