Ecuaciones: interpretación geométrica
En esta página mostramos la interpretación geométrica de una ecuación: las soluciones de una ecuación proporcionan los puntos de corte entre las gráficas de dos funciones. También, explicamos que podemos deducir el número de soluciones de una ecuación según las funciones implicadas. Con ejemplos y problemas resueltos.
Índice:
- Gráfica y puntos de corte
- Ecuación
- Soluciones de la ecuación
- Problemas resueltos
1. Gráfica y puntos de corte
Recordamos que la gráfica de una función \(y = f(x)\) es el conjunto de puntos \((x, f(x))\).
La intersección de la gráfica de dos funciones \(y = f(x)\) e \(y = g(x)\) son los puntos donde las gráficas se cortan.
Ejemplo
La gráfica de \(f(x) = 2x+1\) y la de \(g(x) = x^2-2x+1\) se cortan en los puntos \((0, 1)\) y \((4, 9)\):
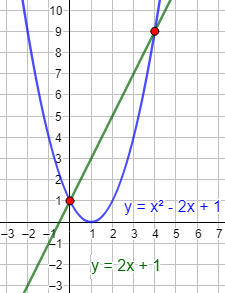
Las dos gráficas se cortan en estos puntos porque coinciden las imágenes de las funciones para \(x=0\) y para \(x = 4\):
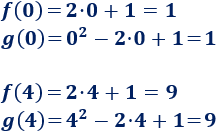
Una forma de hallar las \(x\) para las que dos gráficas se cortan es igualar las expresiones analíticas de las ecuaciones, es decir, resolver la ecuación \(f(x) = g(x)\).
Más información en
2. Ecuación
Comúnmente, se considera la solución de una ecuación como el valor que debe tomar \(x\) para que la igualdad de la ecuación se cumpla. Sin embargo, podemos ver una ecuación como una igualdad entre dos funciones. Para que sea más sencillo de explicar y entender, nos ayudaremos de un ejemplo.
Ejemplo
Sea la ecuación de primer grado
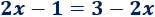
Consideremos esta ecuación como una igualdad entre dos funciones:
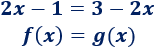
Lógicamente, las funciones \(f\) y \(g\) son
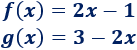
Tal y como hemos comentado anteriormente, la solución de la ecuación \(f(x) = g(x)\) son los valores de \(x\) tales que \(f(x) = g(x)\) y, por ende, las primeras coordenadas de los puntos de corte entre las gráficas de \(f\) y de \(g\).
Resolvemos la ecuación del ejemplo:
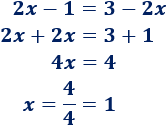
Como la ecuación sólo tiene una solución, las gráficas de \(f\) y de \(g\) se cortan en un único punto: el punto cuya primera coordenada es \(x=1\).
Calculamos la segunda coordenada de dicho punto:
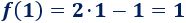
Luego el punto de corte de las gráficas de \(f\) y de \(g\) es (1, 1).
Gráficas:

3. Soluciones de la ecuación
Al considerar una ecuación como una igualdad entre funciones para hallar sus puntos de corte, es fácil ver que pueden darse las siguientes situaciones:
- Una ecuación puede no tener solución (real). Ocurre cuando las dos gráficas no se cortan:
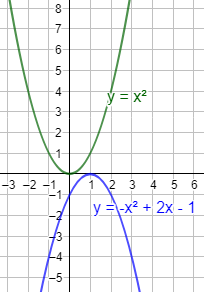
- Una ecuación puede tener una única solución. Ocurre cuando las dos gráficas se cortan en un único punto:
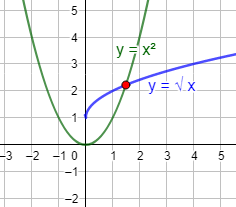
- Una ecuación puede tener varias soluciones. Ocurre cuando las dos gráficas se cortan en varios puntos:
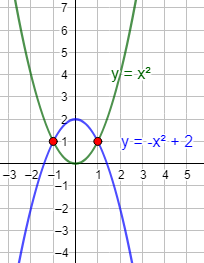
- Una ecuación puede tener infinitas soluciones. Ocurre cuando las dos gráficas son iguales (se cortan en todos sus puntos) o cuando se cortan en infinitos puntos pero no en todos:
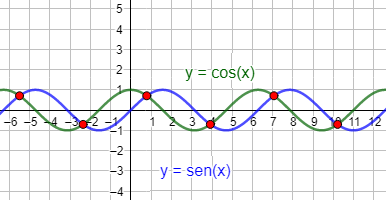
Ahora bien, el número de soluciones dependerá de las funciones implicadas.
Ejemplo
Si ambas gráficas son rectas, sólo caben 3 posibilidades:
- No se cortan (la ecuación no tiene solución) porque las rectas son paralelas:
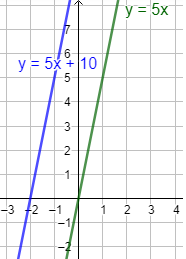
- Se cortan en un solo punto (la ecuación tiene una solución):
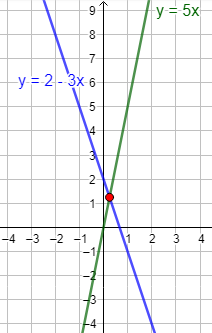
- Se cortan en todos los puntos (la ecuación tiene infinitas soluciones) porque se trata de la misma recta.
4. Problemas resueltos
Problema 1
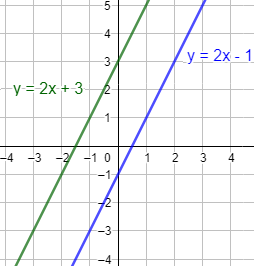
Comprobar que la gráfica de \(f(x) = 2x-1\) y la de \(g(x) = 2x+3\) no se cortan.
Solución:
Como las funciones son rectas con la misma pendiente (\(m=2\)), son rectas paralelas y, por ende, no se cortan. No obstante, vamos a resolver la ecuación \(f(x) = g(x)\):
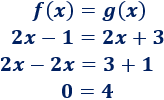
Como obtenemos una igualdad falsa (0 = 4), la ecuación no tiene solución y, por consiguiente, las rectas no se cortan.
Gráficas:
Problema 2
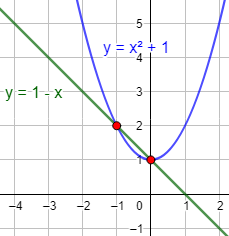
¿En cuántos puntos se cortan las gráficas de \(f(x) = x^2+1\) y \(g(x) = 1-x\)?
Solución:
La función \(f\) es una parábola y \(g\) es una recta. Por tanto, se cortan en 2 puntos, 1 punto o ninguno.
Igualamos las funciones y resolvemos la ecuación:
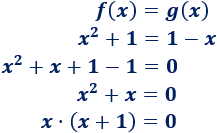
Se trata de una ecuación de segundo grado incompleta con dos soluciones: \(x = 0\) y \(x = -1\). Por tanto, hay dos puntos de corte.
Calculamos la segunda coordenada de los puntos de corte:
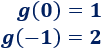
Luego los puntos de corte son \((0,1)\) y \((-1,2)\).
Gráficas:
Problema 3
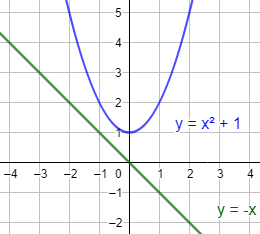
Responder las cuestiones sin resolver la siguiente ecuación:
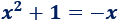
- ¿Puede tener tres soluciones?
- ¿Puede tener infinitas soluciones?
Solución:
La función \(f(x) = x^2 +1\) es una parábola y \(g(x) = -x\) es una recta. Como ya dijimos en el problema anterior, sus gráficas pueden cortarse en 2 puntos, 1 punto o ninguno. Por tanto,
- No puede tener 3 soluciones.
- No puede tener infinitas soluciones (a lo sumo, 2).
Gráficas:
Problema 4
Resolver geométricamente la siguiente ecuación:
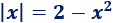
Solución:
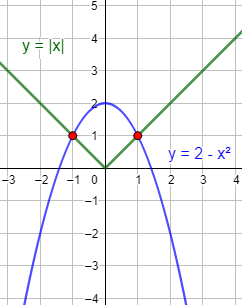
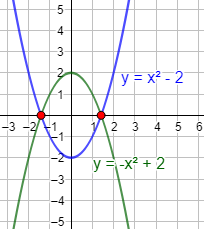
La gráfica de la función \(f(x) = |x|\) está formada por las rectas \(y = -x\) en los negativos e \(y = x\) en los positivos.
La gráfica de \(g(x) = 2-x^2\) es una parábola con forma de \(\cap\) que pasa por el punto \((0,2)\).
Por las formas de las gráficas, ya podemos deducir que la ecuación tiene dos soluciones.
Gráficas:
Observando las gráficas, los dos puntos de corte son
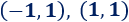
Problema 5
Escribir una ecuación que no tenga solución.
Solución:
Consideremos, por ejemplo, dos parábolas:
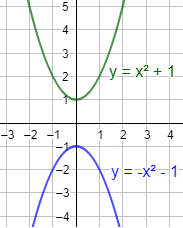
- Una con forma de \(\cup\) situada sobre el eje X. Por ejemplo, \(y = x^2 +1\).
- Una parábola con forma de \(\cap\) situada baja dicho eje. Por ejemplo, \(y = -x^2-1\).
Estas parábolas no pueden cortarse.
Por tanto, la siguiente ecuación no tiene solución (real):
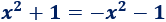
En efecto, si intentamos resolverla, obtenemos la ecuación equivalente \( x^2 = -1\), la cual no tiene soluciones reales:
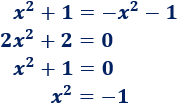
Gráficas:
Problema 6
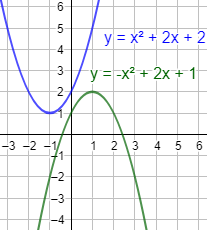
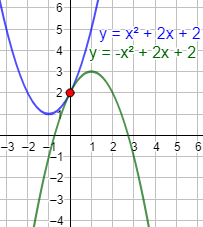
¿Cuántas soluciones puede tener la ecuación \(f(x) = g(x)\) si \(f\) y \(g\) son dos parábolas?
Solución:
Imaginando parábolas en el plano, la ecuación puede tener 2 soluciones, 1 solución o ninguna:
- Dos soluciones:
- Una solución:
- Ninguna solución:
Temas relacionados:
- ¿Qué es una ecuación?
- ¿Todas las ecuaciones tienen solución?
- ¿Cuántas soluciones tiene una ecuación?
- ¿Hay ecuaciones sin solución?
- ¿Por qué se dice al cuadrado y al cubo?
- Pasar de un lado a otro de la igualdad
Problemas y Ecuaciones ©
ISSN 2659-9899