Paralelas y perpendiculares
Explicamos qué son las rectas paralelas y las perpendiculares y cómo identificarlas. Con ejemplos y problemas resueltos.
Índice:
- Introducción
- Paralelas
- Perpendiculares
- Problemas resueltos
1. Introducción
Recordad que la ecuación de una recta es

El coeficiente \(m\) es la pendiente y \(n\) es la ordenada en el origen.
El valor de la pendiente, \(m\), es la causa de un mayor o menor crecimiento.
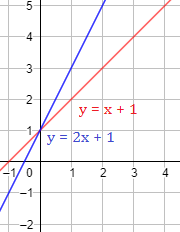
Ejemplo 1
La recta \(y = 2x+1\) crece más rápido que \(y =x+1\) porque tiene una pendiente mayor:
El valor de la ordenada en el origen, \(n\), es la segunda coordenada del punto de corte de la recta con el eje Y.
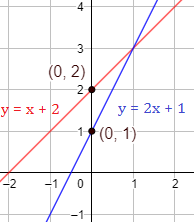
Ejemplo 2
La recta \(y = 2x+1\) corta al eje Y en \((0,1)\) y la recta \(y =x+2\) lo hace en el punto \((0,2)\):
2. Paralelas
Dos rectas son paralelas cuando no se cortan. Esto ocurre cuando las rectas tienen la misma pendiente.
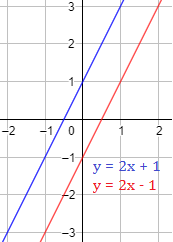
Ejemplo 3
Las rectas \(y = 2x+1\) e \(y =2x-1\) son paralelas. Observad que tienen la misma pendiente, \(m=2\):
3. Perpendiculares
Dos rectas son perpendiculares cuando se cortan formando un ángulo recto (ángulo de 45°).
Esto ocurre cuando la pendiente de una de las rectas es el opuesto del inverso de la otra. Es decir, si la pendiente de una de las rectas es \(m\), la otra debe ser \(-1/m\).
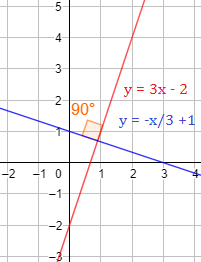
Ejemplo 4
Las rectas \(y = 3x -2\) e \(y = -x/3 + 1\) son perpendiculares:
4. Problemas resueltos
Problema 1
Determinar si las siguientes rectas son o no paralelas o perpendiculares:
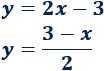
Solución:
La pendiente de la recta \(y=2x-3\) es \(m_1 = 2\).
Podemos reescribir la segunda recta:
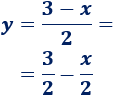
De este modo, vemos mejor que la pendiente es \(m_2 = -1/2\).
Las rectas son perpendiculares porque \(m_2 = -1/m_1\).
Representación:
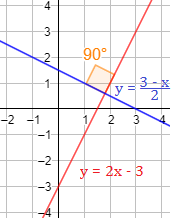
Problema 2
Determinar si las siguientes rectas son o no paralelas o perpendiculares:
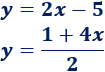
Solución:
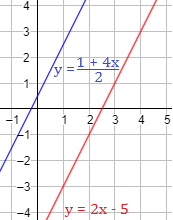
La pendiente de la recta \(y = 2x-5\) es \(m = 2\).
Observad que podemos escribir la segunda recta de otro modo:
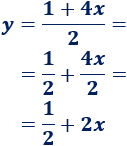
De este modo, se observa que la pendiente de esta recta también es \(m=2\). Por tanto, son rectas paralelas.
Representación:
Problema 3
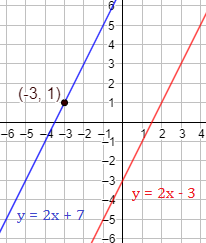
Hallar la recta paralela a la recta \(y = 2x -3\) y que pasa por el punto \((-3,1)\).
Solución:
La ecuación de una recta es

Como la recta que buscamos debe ser paralela a la recta \(y = 2x-3\), su pendiente debe ser la misma. Por tanto, \(m=2\).
Podemos calcular \(n\) sustituyendo las coordenadas del punto \((-3,1)\) en la ecuación de la recta:
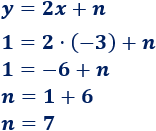
Por tanto, la recta que buscamos es

Representación:
Problema 4
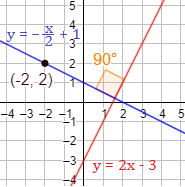
Hallar la recta perpendicular a la recta \(y = 2x -3\) y que pasa por el punto \((-2,2)\).
Solución:
La ecuación de una recta es

Como la recta debe ser perpendicular a \(y = 2x-3\), su pendiente debe ser \(m = -1/2\).
Calculamos \(n\) sustituyendo las coordenadas del punto en la ecuación:
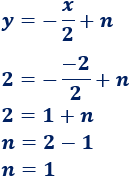
Por tanto, es la recta
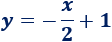
Representación:
Problema 5
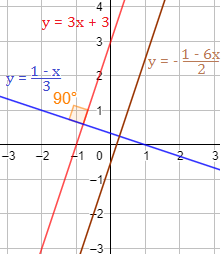
Determinar si las siguientes rectas son perpendiculares a la recta \(y = 3x+3\):
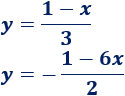
Solución:
Reescribimos la primera ecuación:
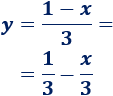
Su pendiente es \(m_1 = -1/3\). Esta recta es perpendicular a \(y = 3x+3\).
Reescribimos la segunda ecuación:
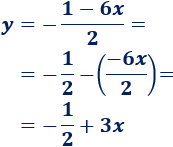
Su pendiente es \(m_2 = 3\). Esta recta es paralela a \(y = 3x+3\).
Representación:
Más problemas similares: rectas paralelas y perpendiculares.