¿Cómo sumar y restar fracciones?
Fracciones con igual denominador
En esta página explicamos cómo sumar y restar fracciones, con ejemplos y representaciones. Antes que nada, recordamos el concepto de fracción; después, explicamos la suma y la resta de fracciones con igual denominador. Finalmente, resolvemos algunos problemas.
Índice:
- Concepto de fracción
- Sumar fracciones
- Restar fracciones
- Problemas resueltos
1. Concepto de fracción
Nombres
Una fracción está formada por dos números separados por una raya:

- El número \(a\) es el numerador.
- El número \(b\) es el denominador y NUNCA puede ser \(0\).
La fracción como división
La fracción \(a/b\) es el cociente de la división \(a\) dividido entre \(b\).
Ejemplo
- La fracción \(10/2\) es igual a \(5\) porque \(10\) dividido entre \(2\) es igual a \(5\):
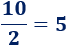
- La fracción \(-3/2\) es igual a \(-1,5\) porque \(-3\) dividido entre \(2\) es igual a \(-1,5\):
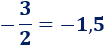
La fracción como partes de un todo
Supongamos que tenemos un cuadrado y lo dividimos en \(4\) cuadrados iguales:
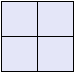
- Cada uno de ellos es un cuarto del cuadrado, es decir, la fracción \(1/4\) (un cuarto) del cuadrado inicial:
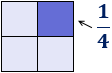
- Dos cuadrados se corresponden con la fracción \(2/4\) (dos cuartos) del cuadrado inicial:
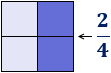
- Tres cuadrados se corresponden con la fracción \(3/4\) (tres cuartos) del cuadrado inicial:
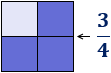
- Cuatro cuadrados se corresponde con la fracción \(4/4\) (cuatro cuartos) del cuadrado inicial:
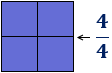
- Nota: observad que la fracción \(4/4\) del cuadrado es la unidad del cuadrado: \(4/4 = 1\). Es decir, es el cuadrado inicial.
En definitiva, la fracción \(a/b\) puede verse como un total de \(a\) trozos tras dividir un todo en \(b\) partes iguales.
2. Sumar fracciones
Seguimos con el ejemplo anterior del cuadrado dividido en cuatro cuadrados iguales:

Consideremos la suma
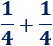
Observando la representación, la suma corresponde a dos de los cuadrados, es decir, corresponde a la fracción \(2/4\):
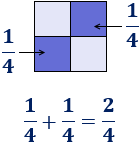
Consideremos ahora la suma
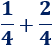
En este caso estamos sumado \(3\) de los cuadrados, con lo que obtenemos la fracción \(3/4\):
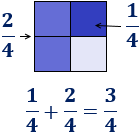
Es fácil ver que la suma de fracciones (con denominador común) se calcula sumando los numeradores:
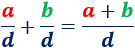
Ejemplos
- Sumamos las fracciones \(2/5\) y \(1/5\):
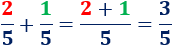
- Sumamos las fracciones \(4/7\) y \(2/7\):
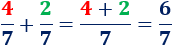
- Sumamos las fracciones \(2/3\) y \(2/3\):
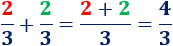
3. Restar fracciones
La resta de fracciones con igual denominador se calcula restando los numeradores:
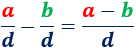
Ejemplos
- Restamos las fracciones \(2/5\) y \(1/5\):
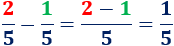
- Restamos las fracciones \(4/7\) y \(2/7\):
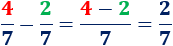
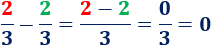
- Restamos las fracciones \(2/3\) y \(2/3\):
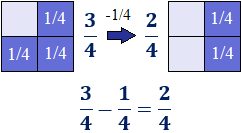
También, podemos ver la resta de fracciones gráficamente. Siguiendo con el ejemplo anterior del cuadrado, consideremos la resta
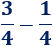
Si tenemos \(3\) de los cuadrados y le restamos \(1\), entonces nos quedan \(2\):
4. Problemas resueltos
Problema 1
Calcular las siguientes sumas de fracciones:
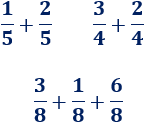
Solución:
Sólo tenemos que sumar los numeradores porque los denominadores son iguales.
Primera suma:
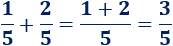
Segunda suma:
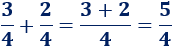
Tercera suma:
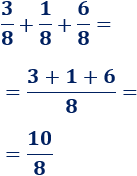
Problema 2
Calcular la siguiente suma de fracciones:
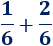
Mediante una representación, comprobar que el resultado es igual a la fracción \(1/2\).
Solución:
La suma de fracciones con igual denominador se calcula sumando los numeradores:
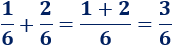
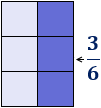
Representación de un rectángulo dividido en \(6\) partes iguales:
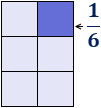
Cada uno de una de las partes es la fracción \(1/6\).
La fracción \(3/6\) son \(3\) de las \(6\) partes:
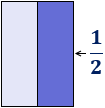
Ahora bien, si en lugar de dividir en rectángulo es \(6\) partes iguales, lo dividimos en \(2\), tenemos
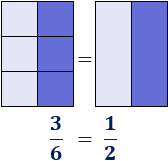
Observad que la fracción \(1/2\) es igual a la fracción \(3/6\):
Problema 3
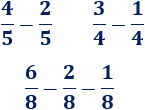
Calcular las siguientes restas de fracciones:
Solución:
Sólo tenemos que restar los numeradores, porque los denominadores son iguales.
Primera resta:
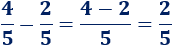
Segunda resta:
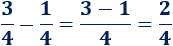
Tercera resta:
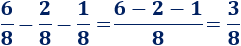
Problema 4
Calcular la siguiente resta de fracciones:
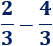
Solución:
Sólo hay que restar los numeradores, pero el resultado es una fracción negativa porque \(2-4 = -2\):
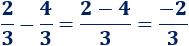
El signo negativo puede escribirse delante de la fracción:
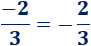
Problema 5
Calcular la siguiente operación con fracciones:
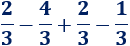
Solución:
Podemos calcular la operación escribiendo todas las sumas y restas en el numerador:
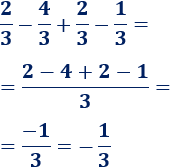
Otros temas relacionados:
- Fracciones equivalentes
- Operaciones con fracciones
- Multiplicar fracciones
- Número por paréntesis
- Paréntesis por paréntesis
- ¿Qué es una ecuación?
- ¿Todas las ecuaciones tienen solución?
- ¿Cuántas soluciones tiene una ecuación?
- ¿Hay ecuaciones sin solución?
- ¿Por qué se dice al cuadrado y al cubo?
- Pasar de un lado a otro de la igualdad
Problemas y Ecuaciones ©
ISSN 2659-9899